История
Сама по себе идея механической передачи восходит к идее колеса. Применяя систему из двух колёс разного диаметра, можно не только передавать, но и преобразовывать движение. Если ведомым будет большее колесо, то на выходе мы потеряем в скорости, но зато крутящий момент этой передачи увеличится. Эта передача удобна там, где требуется «усилить движение», например, при подъеме тяжестей. Но сцепление между передаточными колесами с гладким ободом недостаточно жесткое, колёса проскальзывают. Поэтому вместо гладких колес начали использовать зубчатые.
В Древнем Египте для орошения земель уже использовались приводимые в действие быками устройства, состоявшие из деревянной зубчатой передачи и колеса с большим числом ковшей.
Вместо зубьев первоначально использовали деревянные цилиндрические или прямоугольные пальцы, которые устанавливали по краю деревянных ободьев.
Изготовленный в I веке до н.э. Антикитерский механизм состоял из десятков металлических зубчатых колес .
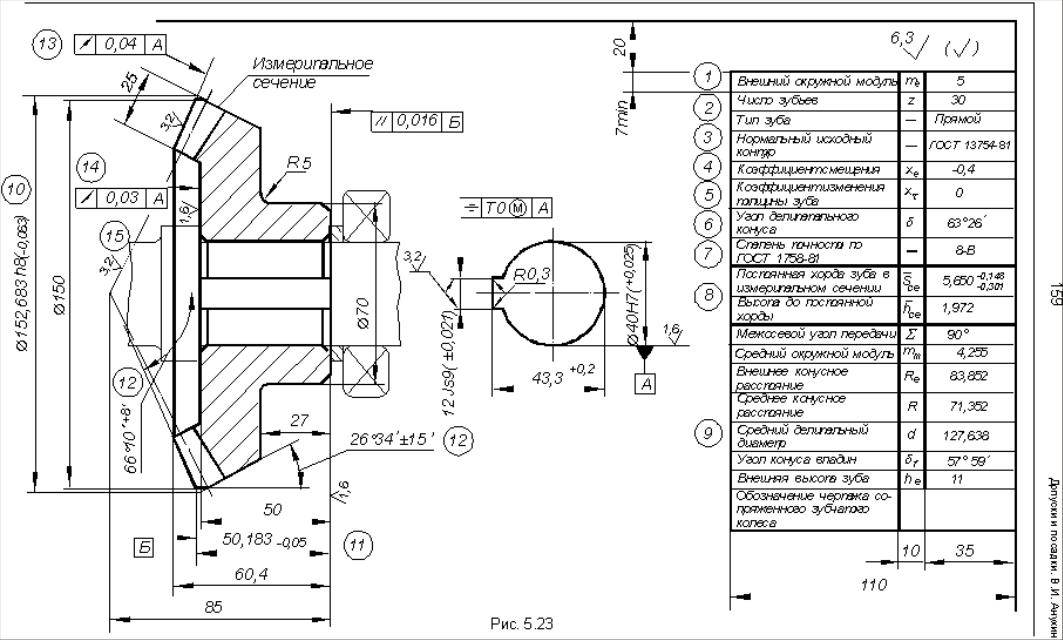
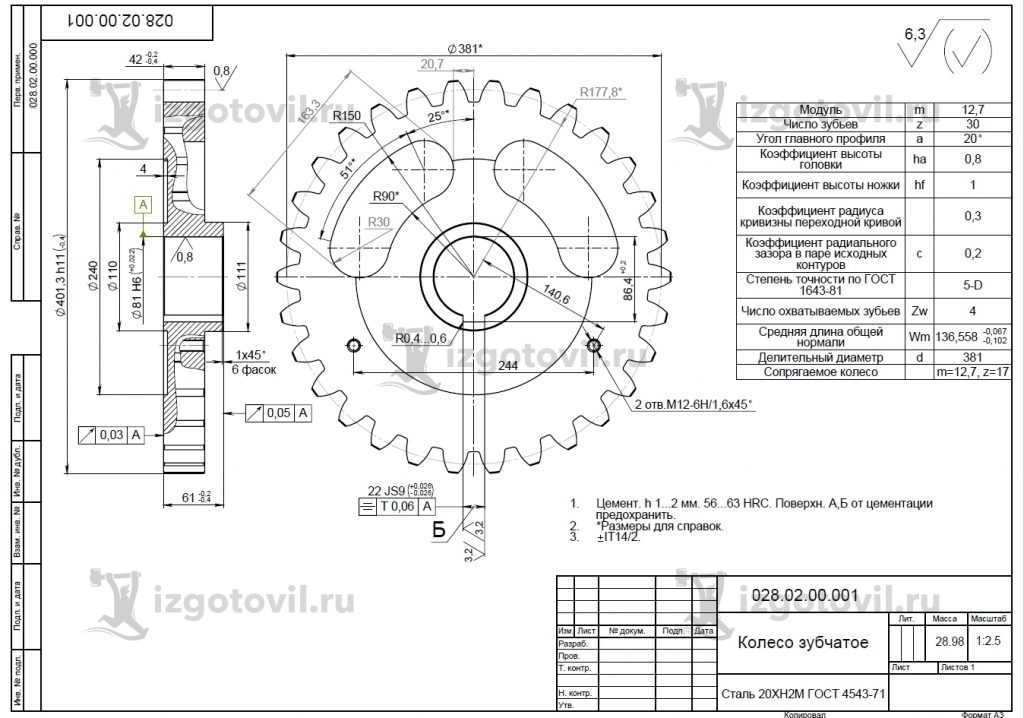
Исходные данные и замеры
На практике перед инженерами часто встает задача определения модуля реально существующей шестерни для ее ремонта или замены. При этом случается и так, что конструкторской документации на эту деталь, как и на весь механизм, в который она входит, обнаружить не удается.
Самый простой метод — метод обкатки. Берут шестерню, для которой характеристики известны. Вставляют ее в зубья тестируемой детали и пробуют обкатать вокруг. Если пара вошла в зацепление — значит их шаг совпадает. Если нет — продолжают подбор. Для косозубой выбирают подходящую по шагу фрезу.
Такой эмпирический метод неплохо срабатывает для зубчатых колес малых размеров.
Для крупных, весящих десятки, а то и сотни килограмм, такой способ физически нереализуем.
Результаты расчетов
Для более крупных потребуются измерения и вычисления.
Как известно, модуль равен диаметру окружности выступов, отнесенному к числу зубов плюс два:
m=De/(z+2)
Последовательность действий следующая:
- измерить диаметр штангенциркулем;
- сосчитать зубцы;
- разделить диаметр на z+2;
- округлить результат до ближайшего целого числа.
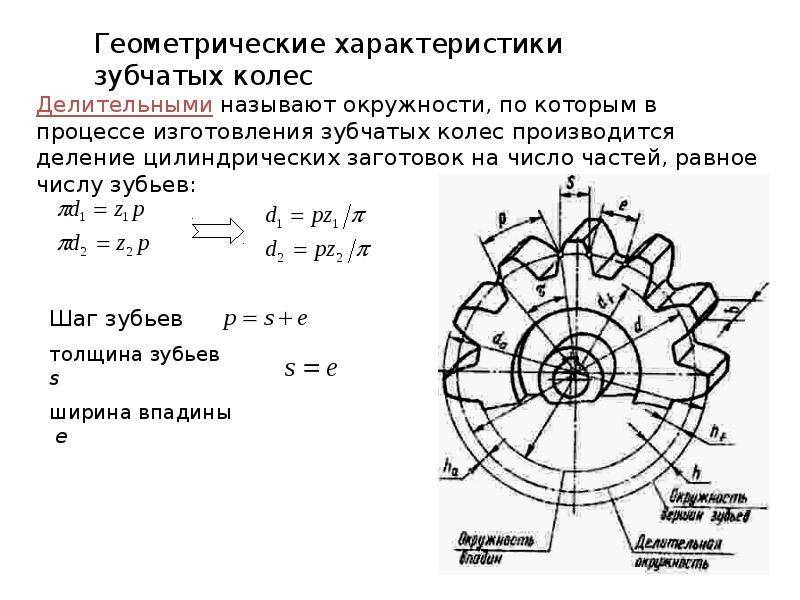
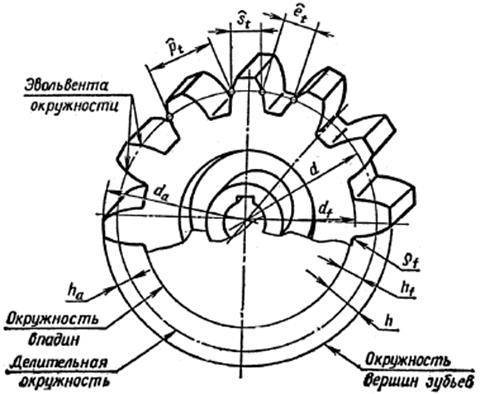
Зубец колеса и его параметры
Данный метод подходит как для прямозубых колес, так и для косозубых.
Сходства и различия шестерен и зубчатых колес
Придерживаясь вышеописанного мнения о разделении шестерен и зубчатых колес на два самостоятельных вида деталей, специалисты все же сходятся во мнении, что у этих элементов есть некоторые сходства:
- и шестерня, и зубчатое колесо могут выполнять функции как ведомого, так и ведущего элемента передачи (что противоречит терминологии межгосударственного стандарта);
- и та, и другая деталь может иметь коническую, либо цилиндрическую поверхность;
- оба элемента одинаково эффективны при эксплуатации в бензо- и электроинструменте;
- шестерни и зубчатые колеса можно использовать для запуска вращательных осей;
- эти виды деталей взаимозаменяемы, они схожи внешне и функционально.
Подобные сходства несколько противоречивы, но все же они встречаются в профессиональной среде. То же самое касается и различий, согласно которым:
- зубчатые колеса применяются только в сложных механизмах, в то время как шестерни являются универсальными элементами;
- шестерни используют исключительно парами, тогда как зубчатое колесо может работать без парного элемента;
- для зубчатых колес характерен больший диаметр, за счет чего эти детали чаще применяются в мощных системах.
Даже исходя из такой точки зрения можно сделать вывод, что шестерни и зубчатые колеса одинаковы по функционалу и в большинстве сфер не имеют формальной разницы.
Чем отличается зубчатое колесо от шестерни
Еще один момент, на который следует обратить внимание. Конечно, в разговорной речи эти понятия идентичны, но с технической точки зрения шестерня отличается от зубчатого колеса. И различие в основном связано не с особенностями конструкции, а функцией, выполняемой в механизме
И различие в основном связано не с особенностями конструкции, а функцией, выполняемой в механизме.
Согласно перечню основных терминов, приведенных в ГОСТ 16530-83, шестерня — зубчатое колесо с меньшим числом зубьев для редукторов и большим числом для мультипликаторов. Если в механизм входят детали с одинаковым количеством зубьев, то шестерней считается ведущая деталь, а зубчатым колесом — ведомая. Отметим, что на практике применяется еще одна разновидность — вал-шестерня, которая представляет собой вал с нарезанными непосредственно на нем зубьями. Все перечисленные детали являются основными элементами механических зубчатых передач.
Основные параметры зубчатых цилиндрических передач
Стандарт распространяется на цилиндрические передачи внешнего зацепления для редукторов и ускорителей, в том числе и комбинированных (коническо-цилиндрических, цилиндро-червячных и др.), выполняемых в виде самостоятельных агрегатов. Стандарт не распространяется на передачи редукторов специального назначения и специальной конструкции Для встроенных передач стандарт является рекомендуемым
Межосевые расстояния
| 1 ряд | 40 | 50 | 63 | 80 | 100 | 125 | — | 160 | — | 200 | — | 250 | — | 315 | — | 400 |
| 2 ряд | — | — | — | — | — | — | 140 | — | 180 | — | 225 | — | 280 | — | 355 | — |
| 1 ряд | — | 500 | — | 630 | — | 800 | — | 1000 | — | 1250 | — | 1600 | — | 2000 | — | 2500 |
| 2 ряд | 450 | — | 560 | — | 710 | — | 900 | — | 1120 | — | 1400 | — | 1800 | — | 2240 | — |
1-й ряд следует предпочитать 2-му
Межосевые расстояния для двухступенчатых несоосных редукторов общего назначения
| Быстроходная ступень | 40 | 50 | 63 | 80 | 100 | 125 | 140 | 160 | 180 | 200 | 225 | 250 | 280 | 315 |
| Тихоходная ступень | 63 | 80 | 100 | 125 | 160 | 200 | 225 | 250 | 280 | 315 | 355 | 400 | 450 | 500 |
| Быстроходная ступень | 355 | 400 | 450 | 500 | 560 | 630 | 710 | 800 | 900 | 1000 | 1120 | 1250 | 1400 | 1600 |
| Тихоходная ступень | 560 | 630 | 710 | 800 | 900 | 1000 | 1120 | 1250 | 1400 | 1600 | 1800 | 2000 | 2240 | 2500 |
Коэффициент запаса прочности при работе зуба двумя сторонами
Например: зубья реверсивных передач или зубья сателлитов в планетарных передачах
| Материал колес и термо- обработка | Отливки стальные и чугунные без термо- обработки | Отливки стальные и чугунные с термо- обработкой | Поковки стальные нормали- зованные или улучшенные | Поковки и отливки стальные с поверх- ностной закалкой (сердцевина вязкая) | Стальные, нормали- зованные или улучшенные, а также с поверх- ностной закалкой | Стальные с объемной закалкой | Стальные, подверг- нутые цементации, азоти- рованию, циани- рованию и др. | Чугунные и пласт- массовые колеса |
| Коэфф. | 1,9 | 1,7 | 1,5 | 2,2 | 1,4 — 1,6 | 1,8 | 1,2 | 1 — 1,2 |
Межосевые расстояния для трехступенчатых несоосных редукторов общего назначения
| Быстроходная ступень | 40 | 50 | 63 | 80 | 100 | 125 | 140 | 160 | 180 | 200 |
| Промежуточная ступень | 63 | 80 | 100 | 125 | 160 | 200 | 225 | 250 | 280 | 315 |
| Тихоходная ступень | 100 | 125 | 160 | 200 | 250 | 315 | 355 | 400 | 450 | 500 |
| Быстроходная ступень | 225 | 250 | 280 | 315 | 355 | 400 | 450 | 500 | 560 | 630 |
| Промежуточная ступень | 355 | 400 | 450 | 500 | 560 | 630 | 710 | 800 | 900 | 1000 |
| Тихоходная ступень | 560 | 630 | 710 | 800 | 900 | 1000 | 1120 | 1250 | 1400 | 1600 |
Номинальные передаточные числа
| 1 ряд | 1,0 | — | 1,25 | — | 1,6 | — | 2,0 | — | 2,5 | — | 3,15 | |
| 2 ряд | — | 1,12 | — | 1,4 | — | 1,8 | — | 2,24 | — | 2,8 | — | |
| 1 ряд | — | 4,0 | — | 5,0 | — | 6,3 | — | 8,0 | — | 10 | — | 12,5 |
| 2 ряд | 3,55 | — | 4,5 | — | 5,6 | — | 7,1 | — | 9,0 | — | 11,2 | — |
1-й ряд следует предпочитать 2-му Фактические значения передаточных чисел не должны отличаться от номинальных более чем на 2,5% при номинальном меньше 4,5 и на 4% при номинальном больше 4,5
Коэффициент ширины зубчатых колес (отношение ширины зубчатого колеса к межосевому расстоянию) должен соответствовать: 0,100; 0,125; 0,160; 0,200; 0,315; 0,400; 0,500; 0,630; 0,800; 1,0; 1,25
Численные значения ширины зубчатых колес округляются до ближайшего числа из ряда Ra20 по ГОСТу 6636.
При различной ширине сопряженных зубчатых колес значение коэффициента ширины зубчатых колес относится к более узкому из них.
Что представляет собой шестерня
Шестерня – это небольшое колесико с зубьями, которое крепится к специальной вращающейся оси. Поверхность у шестеренки в данном случае может быть как конической, так и цилиндрической.
Шестеренчатые передачи также имеют свою классификацию:
- Прямозубые. Наиболее распространенный вид шестеренок, у которых зубья зачастую располагаются в радиальных плоскостях.
- Скошенные. По-другому этот тип называется еще косозубым, а его использование в ходу у бензо- и электрических инструментов. По отношению к вращающейся оси они находятся под определенным углом.
- Червячные. Их еще называют спиральными шестернями, которые используются преимущественно для рулевого управления автомобилем.
- Винтовые. Они имеют зачастую форму цилиндра, а также расположены по всей линии винта. Располагаются такие шестеренки на валах, которые расположены перпендикулярно к вращающейся оси.
Данные разновидности являются наиболее распространенными, однако далеко не единственными, поэтому используемый вид напрямую соотносится с тем, какую функцию он должен будет выполнять.
При этом каждая шестеренка имеет определенное количество зубьев, что определяется ее назначением. Разница между количеством используемых зубьев необходима, поскольку благодаря этому фактору появляется возможность регулировать обороты вала и крутящийся момент. Шестеренки также разделяются на ведущие и ведомые. Ведущей называется та шестерня, к которой вращательный момент подводится снаружи, а ведомой – та, с которой она снимается.
Почему шестеренку называют так?
Технически это понятно. Изначально «шестерёнка» — самое маленькое колесо в зубчатой передаче. Меньше шести зубьев там не бывает даже в теории, захват не обепечивается. … В машиностроении ведомое колесо зубчатой передачи редуктора называется колесом».
Формула расчета параметров прямозубой передачи
Чтобы определить параметры прямозубой шестеренки, потребуется выполнить некоторые предварительные вычисления. Длина начальной окружности равна π×D, где D — ее диаметр.
Расчет модуля зубчатого колеса
Шаг зацепления t – это расстояние между смежными зубами, измеренное по начальной окружности. Если это расстояние умножить на число зубов z, то мы должны получить ее длину:
проведя преобразование, получим:
Если разделить шаг на число пи, мы получим коэффициент, постоянный для данной детали зубчатой передачи. Он и называется модулем зацепления m.
размерность модуля шестерни — миллиметры. Если подставить его в предыдущее выражение, то получится:
выполнив преобразование, находим:
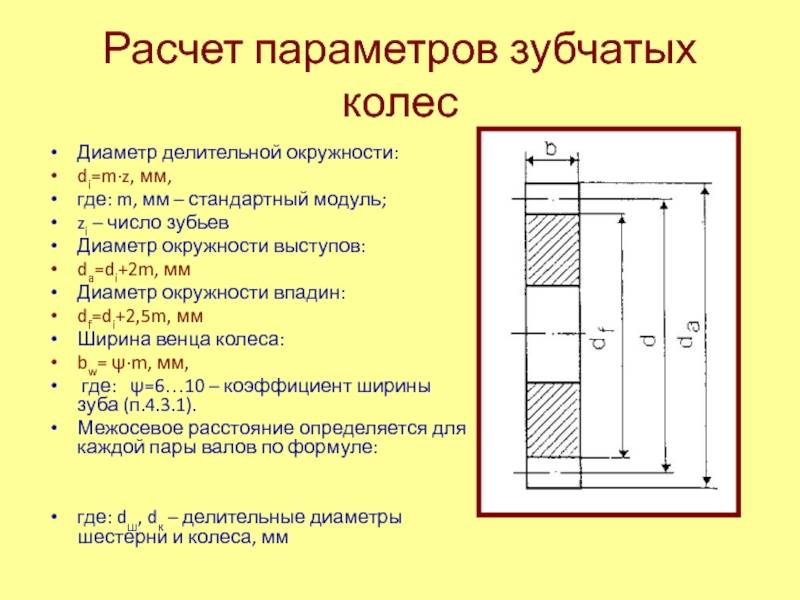
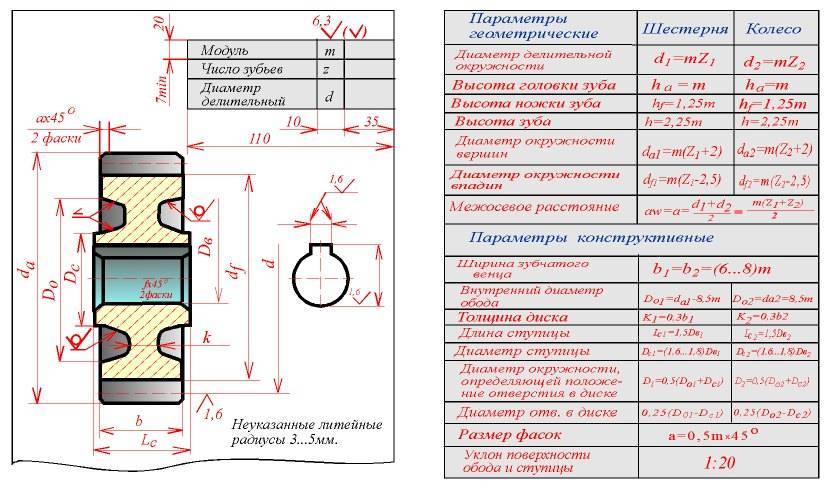
Отсюда вытекает физический смысл модуля зацепления: он представляет собой длину дуги начальной окружности, соответствующей одному зубцу колеса. Диаметр окружности выступов De получается равным
где h’- высота головки.
Высоту головки приравнивают к m:
Проведя математические преобразования с подстановкой, получим:
Диаметр окружности впадин Di соответствует De за вычетом двух высот основания зубца:
где h“- высота ножки зубца.
Для колес цилиндрического типа h“ приравнивают к значению в 1,25m:
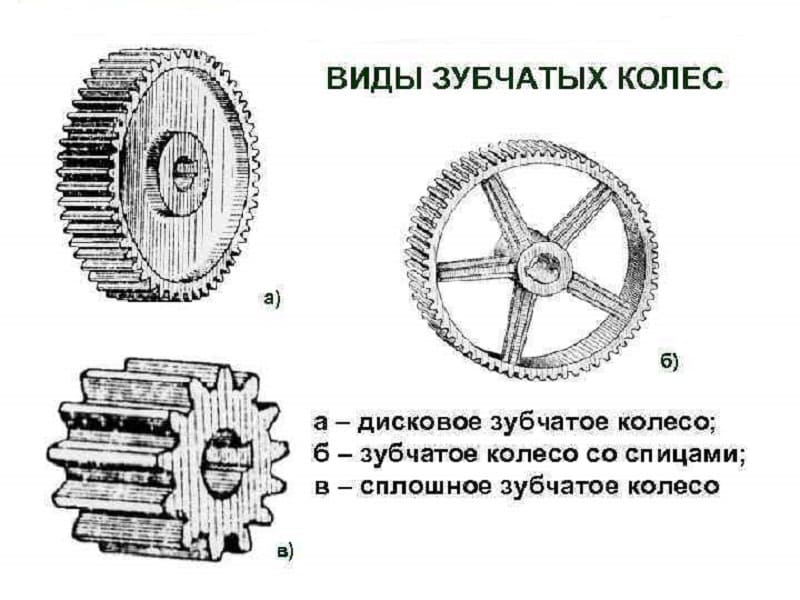
Устройство зубчатого колеса
Выполнив подстановку в правой части равенства, имеем:
что соответствует формуле:
и если выполнить подстановку, то получим:
Иначе говоря, головка и ножка зубца относятся друг к другу по высоте как 1:1,25.
Следующий важный размер, толщину зубца s принимают приблизительно равной:
- для отлитых зубцов: 1,53m:
- для выполненных путем фрезерования-1,57m, или 0,5×t
Поскольку шаг t приравнивается к суммарной толщине зубца s и впадины sв, получаем формулы для ширины впадины
- для отлитых зубцов: sв=πm-1,53m=1,61m:
- для выполненных путем фрезерования- sв= πm-1,57m = 1,57m
Характеристики конструкции оставшейся части зубчатой детали определяются следующими факторами:
- усилия, прикладываемые к детали при эксплуатации;
- конфигурация деталей, взаимодействующих с ней.
Детальные методики исчисления этих параметров приводятся в таких ВУЗовских курсах, как «Детали машин» и других. Модуль шестерни широко используется и в них как один из основных параметров.
Для отображения шестеренок методами инженерной графики используются упрощенные формулы. В инженерных справочниках и государственных стандартов можно найти значения характеристик, рассчитанные для типовых размеров зубчатых колес.
Механическое преимущество: крутящий момент против скорости вращения
Зубчатые передачи работают по принципу механического преимущества. Это значит, что с помощью использования шестерен различных диаметров вы можете изменять скорость вращения выходного вала и вращающий момент, развиваемый приводным двигателем.
Любой электродвигатель имеет определенную скорость вращения и соответствующий его мощности крутящий момент. Но, к сожалению, для многих механизмов предлагаемые на рынке и подходящие по стоимости асинхронные двигатели обычно не обладают желаемым соотношением между скоростью и моментом (исключением являются сервоприводы и мотор-редукторы с высоким моментом). Например, вы действительно хотите, чтобы колеса вашего робота-уборщика вращались со скоростью 3000 об/мин при низком крутящем моменте? Нет конечно, поэтому последний зачастую предпочтительнее скорости.

Общее определение
Наглядный пример изменения числа оборотов проще всего наблюдать на простом велосипеде. Человек медленно крутит педали. Колесо вращается значительно быстрее. Изменение количества оборотов происходит за счет 2 звездочек, соединенных в цепь. Когда большая, вращающаяся вместе с педалями, делает один оборот, маленькая, стоящая на задней ступице, прокручивается несколько раз.
Передачи с крутящим моментом
В механизмах используют несколько видов передач, изменяющих крутящий момент. Они имеют свои особенности, положительные качества и недостатки. Наиболее распространенные передачи:
Ременная передача самая простая в исполнении. Используется при создании самодельных станков, в станочном оборудование для изменения скорости вращения рабочего узла, в автомобилях.
Ремень натягивается между 2 шкивами и передает вращение от ведущего в ведомому. Производительность низкая, поскольку ремень скользит по гладкой поверхности. Благодаря этому, ременной узел является самым безопасным способом передавать вращение. При перегрузке происходит проскальзывание ремня, и остановка ведомого вала.
Передаваемое количество оборотов зависит от диаметра шкивов и коэффициента сцепления. Направление вращения не меняется.
На ремне имеются выступы, на шестерне зубчики. Такой тип ремня расположен под капотом автомобиля и связывает звездочки на осях коленвала и карбюратора. При перегрузе ремень рвется, так как это самая дешевая деталь узла.
Цепная состоит из звездочек и цепи с роликами. Передающееся число оборотов, усилие и направление вращения не меняются. Цепные передачи широко применяются в транспортных механизмах, на конвейерах.
Характеристика зубчатой передачи
В зубчатой передаче ведущая и ведомая детали взаимодействуют непосредственно, за счет зацепления зубьев. Основное правило работы такого узла – модули должны быть одинаковыми. В противном случае механизм заклинит. Отсюда следует, что диаметры увеличиваются в прямой зависимости от количества зубьев. Одни значения можно в расчетах заменить другими.
Например, между осями или точками на эвольвенте по средней линии Размер модуля состоит из ширины зуба и промежутка между ними. Измерять модуль лучше в точке пересечения линии основания и оси зубца. Чем меньше радиус, тем сильнее искажается промежуток между зубьями по наружному диаметру, он увеличивается к вершине от номинального размера. Идеальные формы эвольвенты практически могут быть только на рейке. Теоретически на колесе с максимально бесконечным радиусом.
Деталь с меньшим количеством зубьев называют шестерней. Обычно она ведущая, передает крутящий момент от двигателя.

Зубчатое колесо имеет больший диаметр и в паре ведомое. Оно соединено с рабочим узлом. Например, передает вращение с необходимой скоростью на колеса автомобиля, шпиндель станка.
Обычно посредством зубчатой передачи уменьшается количество оборотов и увеличивается мощность. Если в паре деталь, имеющая больший диаметр, ведущая, на выходе шестерня имеет большее количество оборотов, вращается быстрее, но мощность механизма падает. Такие передачи называют понижающими.
Зачем нужна паразитка
При взаимодействии шестерни и колеса происходит изменение сразу нескольких величин:
- количества оборотов;
- мощности;
- направление вращения.
Только в планетарных узлах с нарезкой зубьев по внутреннему диаметру венца сохраняется направление вращения. При наружном зацеплении ставится две одинаковые шестерни подряд. Их взаимодействие не меняет ничего, кроме направления движения. В этом случае обе зубчатые детали называются шестернями, колеса нет. Вторая, промежуточная, получила название «паразитка», поскольку в вычислениях не участвует, меняет только знак.

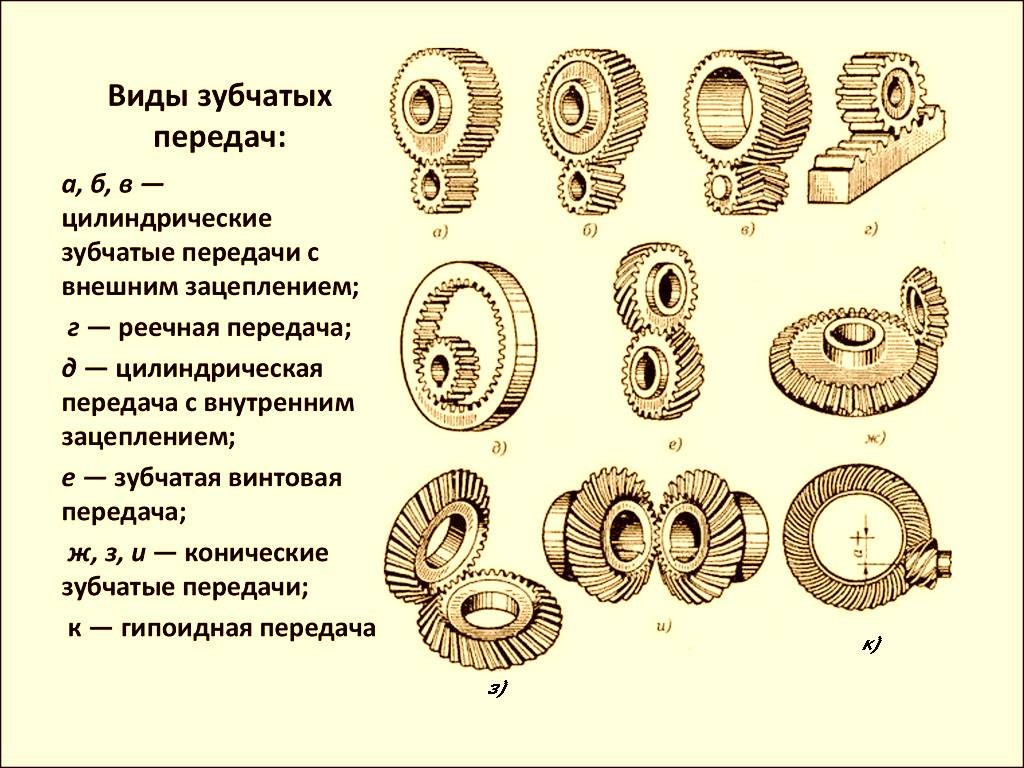
Виды зубчатых соединений
Зубчатое зацепление может иметь различную форму зуба на деталях. Это зависит от исходной нагрузки и расположения осей сопрягаемых деталей. Различают виды зубчатых подвижных соединений:
Самое распространенное и простое в исполнении прямозубое зацепление. Наружная поверхность зуба цилиндрическая. Расположение осей шестерни и колеса параллельное. Зуб расположен под прямым углом к торцу детали.
Передаточное число зубчатой передачи
Мы записали уравнения, но как механически поменять местами крутящий момент и скорость? Для этого нужны две шестерни (иногда больше) различных диаметров, чтобы иметь конкретное передаточное число. В любой паре шестерен большее зубчатое колесо будет двигаться более медленно, чем меньшее, но оно будет передавать на выходной вал больший крутящий момент. Таким образом, чем больше величина разницы (или передаточное число) между двумя колесами, тем больше разница их скоростей и передаваемых крутящих моментов.
Передаточное число показывает, во сколько раз зубчатая передача изменяет скорость и вращающий момент. Для него, опять же, имеется очень простое уравнение.
Предположим, что передаточное число равно 3/1. Это будет означать, что вы увеличиваете ваш крутящий момент втрое, а скорость втрое снижаете.
Пример:
Момент входной = 1,5 Н∙м, Скорость входная = 100 об/с,
Передаточное число = 2/3
Момент выходной = Момент входной * 2/3 = 1 Н∙м,
Скорость выходная = Скорость входная * 3/2 = 150 об/с.
Итак, на выходе передачи момент в полтора раза вырос, а скорость точно так же снизилась.
Зубчатые передачи
Зубчатые передачи — это механизм или часть механизма механической передачи, в состав которого входят зубчатые колёса. Зубчатые передачи служат для того, чтобы непрерывно передавать силу и крутящий момент двух валов, расположение которых определяет тип имеющейся зубчатой передачи. Вот о том, что представляют зубчатые передачи, мы и поговорим в этой статье.
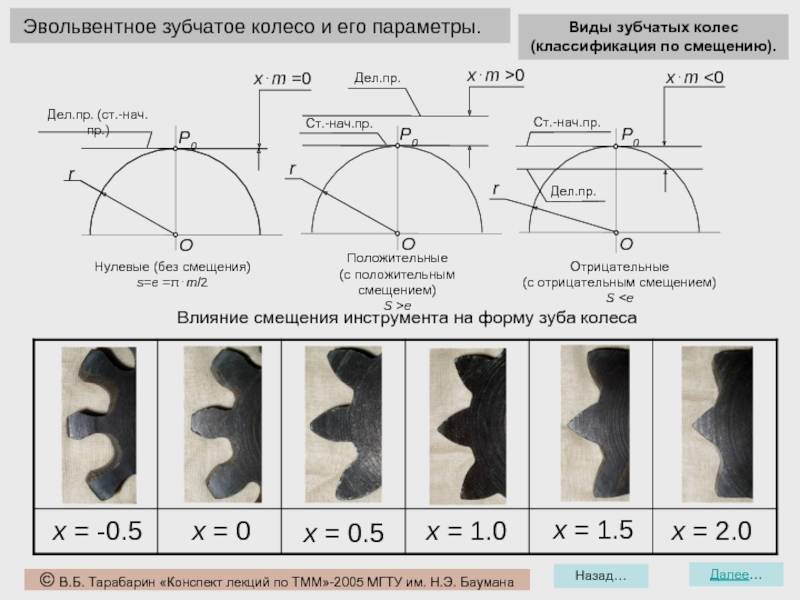
Эвольвентное зацепление
Все прямозубые цилиндрические передачи с одинаковым модулем зацепления могут изготавливаться на одном оборудовании, независимо от количества зубьев и размеров головки.
Модули зацепления цилиндрических и конических зубчатых колес стандартизированы по DIN 780; модули зацепления червячных передач по DIN 780; модули шлицевых соединений по DIN 5480; модули зубчатого зацепления нормального профиля для шестерен со спиральными зубьями по DIN 780.
Форма зубьев
Для прямозубых цилиндрических передач форма зубьев определяется DIN 867, DIN 58400; конических передач — DIN 3971; червячных передач — DIN 3975; шлицевых соединений — DIN 5480 (см. рис. «Прямые и косые зубья (наружное зацепление)» ).
Форма зубьев гипоидных передач регламентируется стандартом DIN 867. В дополнение к стандартным углам зацепления (20° для зубчатых передач и 30° для шлицевых соединений) применяются также и углы зацепления 12°, 14°30 15°, 17°30′| 22°30′ и 25°.
Коррегирование зубчатого зацепления
Коррегирование зубчатого зацепления (изменение высоты головки зуба (см. рис. «Коррегирование зубчатого зацепления прямозубой цилиндрической передачи (циклоидное зацепление)» ) применяется для предотвращения подрезания у шестерен с малым количеством зубьев. Оно позволяет увеличить прочность ножки зуба и точно обеспечить межосевое расстояние.
Зубчатые передачи с точно заданным межосевым расстоянием
У зубчатых пар с точно заданным межосевым расстоянием изменение высоты головки зуба для шестерни и зубчатого колеса производится на одинаковую величину, но в противоположных направлениях, что позволяет сохранить межосевое расстояние неизменным. Такое решение применяется в гипоидных и косозубых передачах.
Зубчатые передачи с изменяемым межосевым расстоянием
Изменение высоты головки зуба для шестерни и зубчатого колеса производится независимо друг от друга, поэтому межосевое расстояние передачи может изменяться. Допускаемые отклонения линейных размеров зубчатых передач регламентированы. Для прямозубых цилиндрических передач — DIN 3960, DIN 58405; для конических передач — DIN 3971; червячных передач — DIN 3975.
Подставляя jη = 0 в приведенные ниже формулы, рассчитывают параметры зацепления без зазора между зубьями. Для определения зазора между зубьями допускаемые отклонения толщины зубьев и зоны их зацепления принимают в соответствии со стандартами DIN 3967 и DIN 58405 в зависимости от требуемой степени точности зубчатой передачи.
Следует отметить, что не обязательно стремиться к нулевому зазору между зубьями. Для компенсации имеющихся отклонений размеров зубьев и сборки шестерен достаточно иметь минимальный зазор, который, кроме того, предотвращает возможность заклинивания зубчатых колес.
Допускаемые отклонения других расчетных параметров (зазор между ножками двух смежных зубьев, межцентровое расстояние) приведены в стандартах DIN 3963, DIN 58405, DIN 3962 Т2, DIN 3967, DIN 3964.
В чем заключаются сходства между шестерней и зубчатым колесом
Между шестерней и зубчатым колесом можно отметить несколько схожих моментов:
- Как и шестерня, зубчатое колесо может быть как ведомым, так и ведущим элементом в общей системе.
- У шестерни и у зубчатого колеса форма может быть как цилиндрической, так и конической, все зависит от той функции, которую конкретная деталь выполняет.
- При помощи шестеренки и зубчатого колеса можно маневрировать на почве скорости вращательного элемента, либо уменьшая ее, либо увеличивая.
- Шестеренки и зубчатые колеса одинаково эффективно можно использовать на электрических и бензоинструментах, однако больше всего используют именно шестеренки, так как они обеспечивают устойчивость механизма.
- Шестеренка и зубчатое колесо могут использоваться для запуска вращательных осей.
Внешние сходства между шестеренкой и зубчатым колесом обоснованы также еще тем, что зачастую эти два элемента могут выполнять схожие функции и быть взаимозаменяемыми в определенных системах и механизмах.
Особенности зубчатых колес и шестерен
И зубчатое колесо, и шестерня имеют вид диска с зубьями, расположенными на конической или цилиндрической поверхности. Эти детали используются в механизмах для преобразования и передачи крутящего момента. Изготовление шестерен и зубчатых колес возможно несколькими способами: методом обката, копированием, горячим и холодным накатыванием. Традиционно зубчатые колеса и шестерни используются парами, в зацеплении одна деталь становится ведущей, а вторая – ведомой. И вот здесь кроется главное различие элементов: ведущую деталь часто называют шестерней, а ведомую – зубчатым колесом. То есть разница основывается на роли элемента в работе механизма, но конструктивно шестерни и зубчатые колеса остаются одинаковыми деталями.
Также при парном зацеплении двух зубчатых колес шестерней называют ту деталь, которая имеет большее число зубьев. То, что зубчатые колеса и шестерни – понятия синонимичные, подтверждает и ГОСТ 16530-83: в определении шестерни указано, что она является ведущим зубчатым колесом передачи (при равном количестве зубьев на обеих деталях) или же колесом с меньшим числом зубьев.
Несмотря на это, некоторые специалисты (особенно работающие в специфических областях) считают необходимым строго разделять понятия шестерни и зубчатого колеса. Для них производство зубчатых колес и изготовление шестерен – принципиально разные процессы, а сами детали имеют свои сходства и различия.
Уравнение зубчатой передачи
Она обменивает высокую входную скорость на больший выходной крутящий момент. Этот обмен происходит по очень простому уравнению, которое можно записать так:
Момент входной * Скорость входная = Момент выходной * Скорость выходная
Скорость входную можно найти, просто просматривая табличку приводного электродвигателя. Момент входной легко определить по этой скорости и механической мощности из той же таблички. Затем просто подставим выходную скорость или требуемый крутящий момент в правую часть уравнения.
Например, предположим, что ваш асинхронный двигатель при моменте на выходном валу 0,5 Н∙м имеет скорость 50 об/с, но вы хотите только 5 об/с. Тогда ваше уравнение будет выглядеть так:
0,5 Н∙м * 50 об/с = Момент выходной* 5 об/с.
Ваш выходной крутящий момент будет 5 Н∙м.
Теперь предположим, что с тем же мотором вам нужно 5 Н∙м, но при этом требуется минимальная скорость 10 об/с. Как бы узнать, способен ли на это ваш мотор вместе с зубчатой передачей (т. е., по сути, мотор-редуктор)? Обратимся снова к нашему уравнению
0,5 Н∙м * 50 об/с = 5 Н∙м * Скорость выходная,
Скорость выходная = 5 об/с.
Итак, вы определили, используя простое уравнение, что при показателе Момент выходной =5 Н∙м обеспечить скорость выходную в 10 об/с ваша зубчатая передача не способна. Вы только что сохранили себе кучу денег, так как не потратили их на механизм, который никогда не заработал бы.
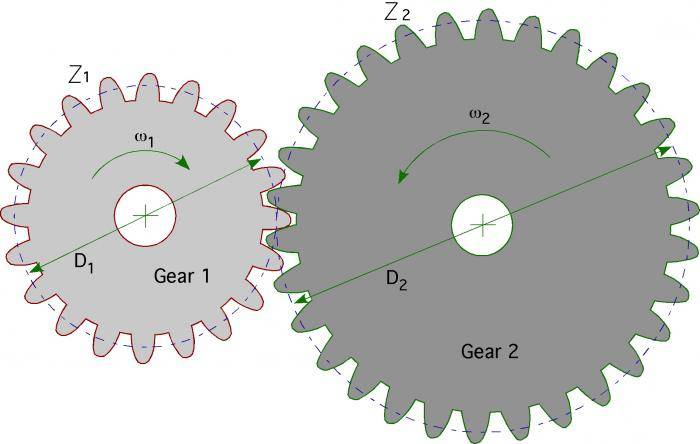
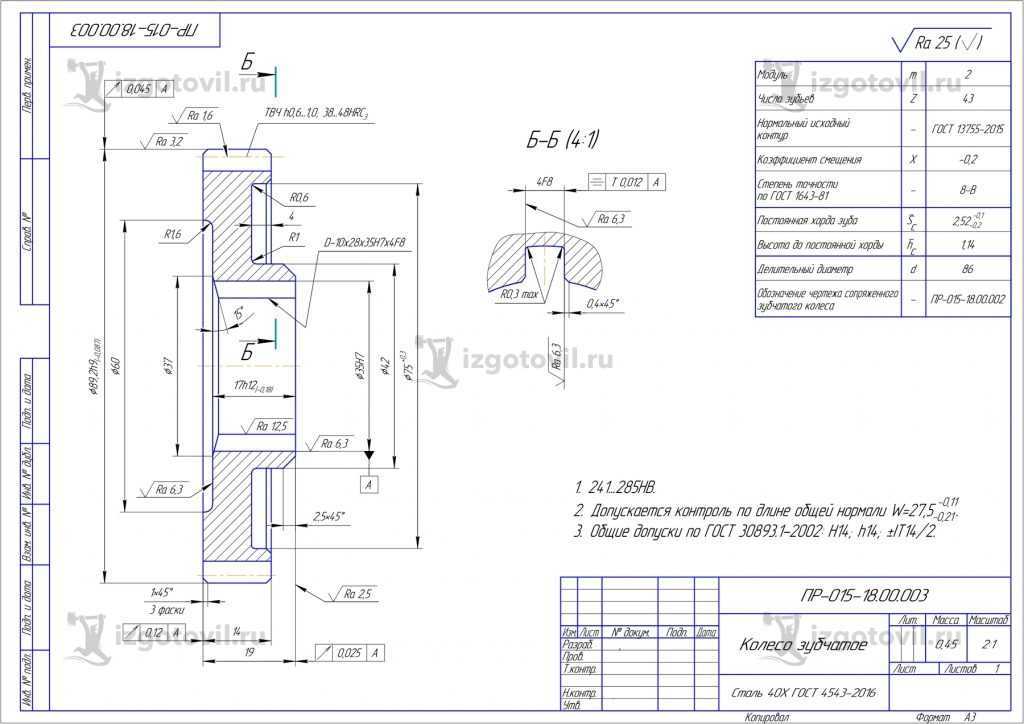
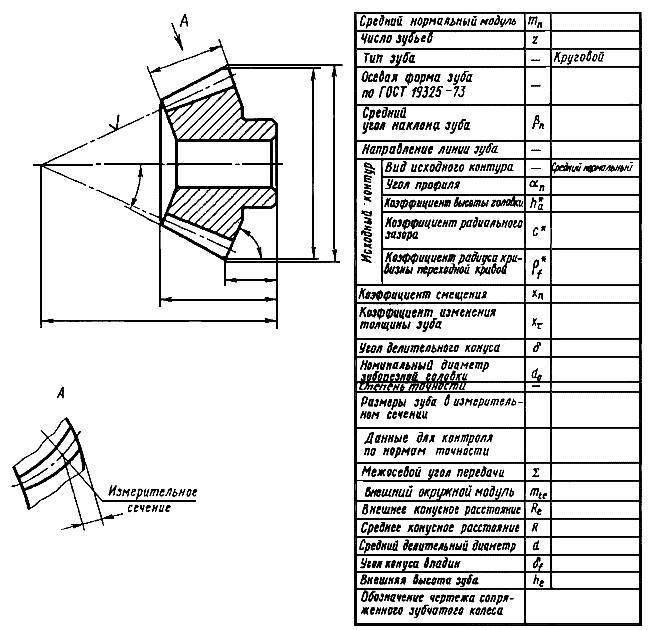
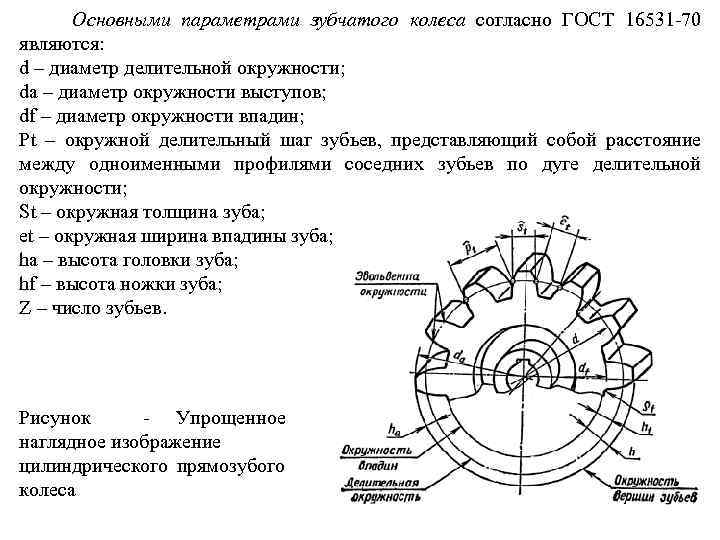
Основные параметры
Для обеспечения подвижности и работоспособности, конструкция отдельных деталей механической передачи должна быть согласована по размерам и геометрии. Для этого при описании подобных устройств принято использовать систему специальных параметров. В их число входят геометрические, массогабаритные и прочностные величины, закрепленные стандартами. Применение стандартных параметров позволяет сравнительно просто производить расчет унифицированных зубчатых передач и обеспечивает гарантированное сопряжение всех изделий между собой. Естественно, что для разных видов, параметры будут несколько отличаться. Далее рассматриваются термины, связанные с конструкцией эвольвентного цилиндрического колеса. Эти параметры, в своем большинстве, описывают основные характеристики и других вариантов колес.
В основе сечения зуба большинства шестерен лежит эвольвентный профиль, который получается на основе одноименной кривой. Его применение легко стандартизируется, характеризуется высокой технологичностью изготовления и низкими требованиями к качеству сборки механизма. Основными параметры эвольвентного зубчатого колеса считаются модуль зацепления и количество зубьев зубчатого колеса. При одном и том же наружном диаметре деталей значения этих величин могут существенно отличаться в разных вариантах конструкции.

Число зубьев определяет коэффициент передачи и геометрические размеры зубьев. На ведущем колесе редуктора оно выполняется меньшим, чем на ведомом. В итоге один нормальный оборот ведущей шестерни приводит к повороту ведомого колеса только на определенный угол. Отношение числа зубьев двух колес дает значение передаточного коэффициента. Размеры зубьев определяются как отношение их количества к длине окружности колеса. С целью упрощения расчетов и гарантированного обеспечения зацепления между разными колесами, предусмотрен дополнительный параметр, называемый модулем зацепления. Любые шестерни с одинаковым модулем обеспечивают взаимодействие между собой и могут использоваться для построения механизмов, без дополнительной обработки.
Сумма ширины зуба и впадины совместно дают шаг зубчатого колеса. Учитывая неравномерность профиля по радиусу и зависимость длины дуги от диаметра, в каждом колесе можно определить бесконечное число значений этого параметра. С целью стандартизации принято рассматривать шаг по делительной окружности, называемый так же окружным шагом. Отношение этого шага к числу пи дает модуль зацепления. В некоторых случаях для описания шестерен используют угловой шаг, измеряемый в градусах. Стандартами предусмотрены и несколько других угловых величин. Например, для упрощения настройки оборудования при изготовлении колес рассматривают угловую ширину зуба и угловую ширину впадины. Определяются они также на основе делительной окружности.