Эвольвентное зубчатое зацепление

Определение скоростей и угловых скоростей звеньев механизма.

1. Известны длины звеньев механизма, величина и направление угловой скорости
ведущего звена, Расчет начинаем вести с ведущего звена механизма. Установив вид
движения звена, записываем соответствующую зависимость. В нашем случае кривошип
совершает вращательное движение.

Угловая скорость постоянна, поэтому скорость точки А определяется по
формуле:

где
. Из
точки О, которая называется полюсом плана скоростей, откладываем
перпендикулярно ОА отрезок оа, соответствующий скорости точки А.

.
Так как для решения задачи будем использовать графический метод, то вводим
масштаб скорости:

.
Для определения скорости точки В записывается векторное уравнение , связывающее
скорости точек А и В , используя теорему о сложении скоростей в переносном и
относительных движениях.

Здесь
и далее одной чертой подчеркнута скорость известная по направлению, и двумя
чертами – скорость, известная по величине и направлению.

Уравнение
имеет однозначное решение, если в нем два неизвестных. Поэтому на
предварительном этапе необходимо зафиксировать четыре параметра из шести. В
данном случае это удается сделать.

Строим
план скоростей. Из точки o проводим направление скорости V_B, а из точки а – направление V_BA.
Точка пересечения этих линий b определяет величины неизвестных скоростей:

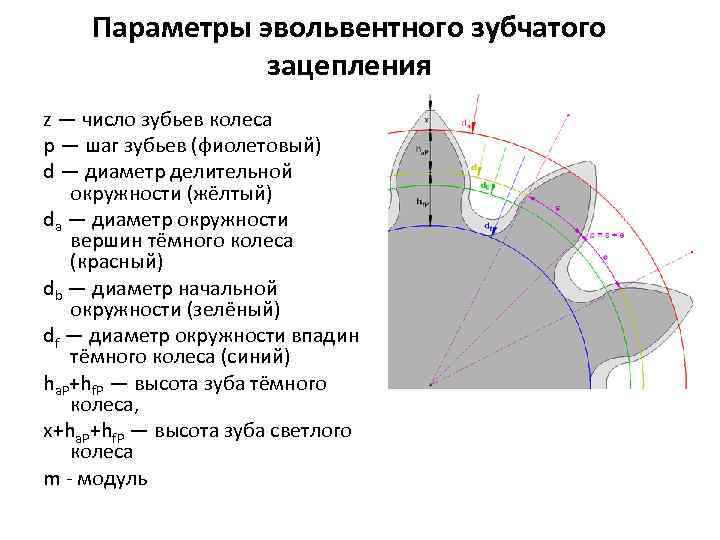
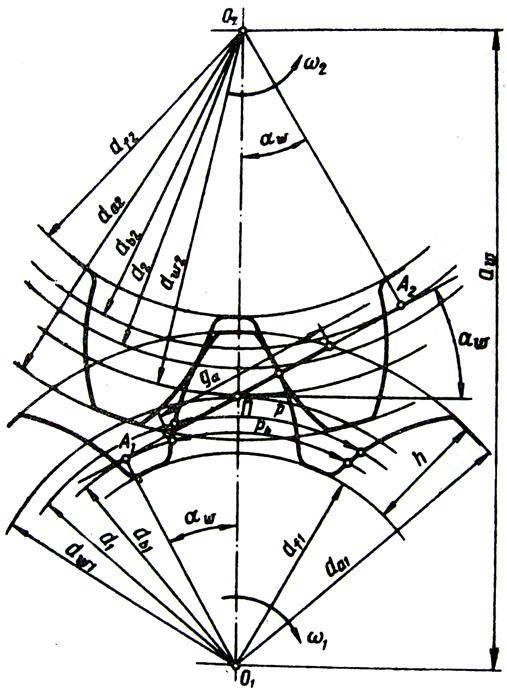
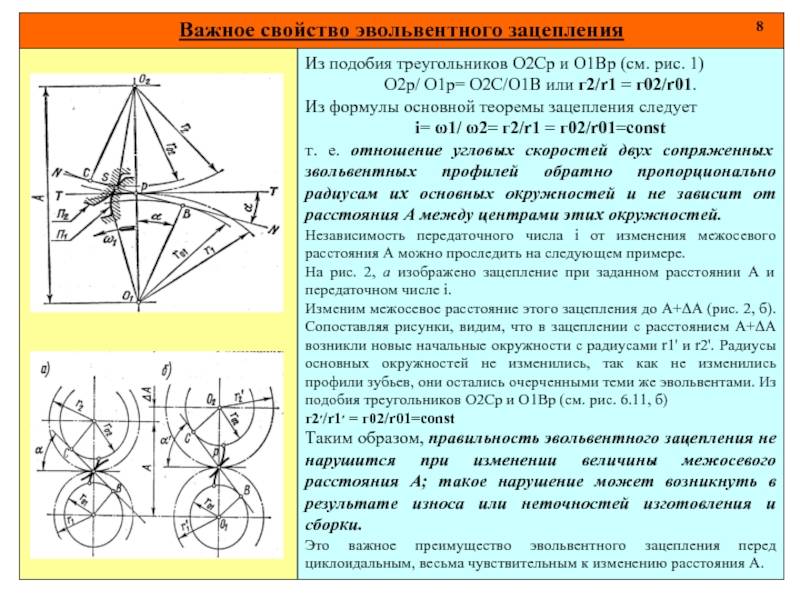
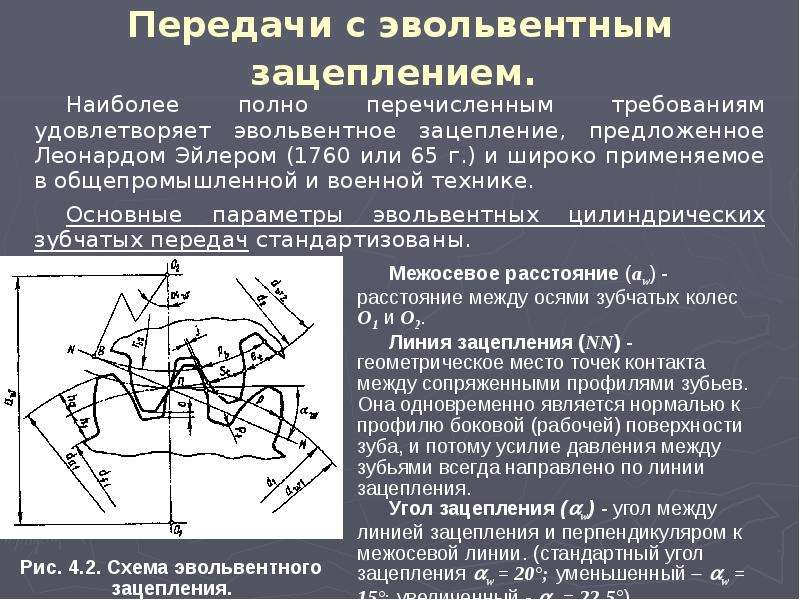
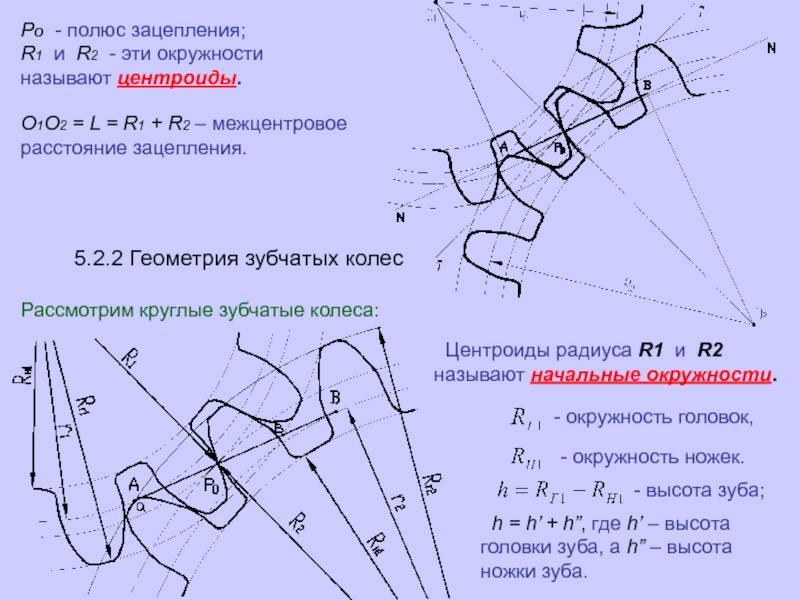
Основные параметры зубчатых цилиндрических передач

Стандарт распространяется на цилиндрические передачи внешнего зацепления для редукторов и ускорителей, в том числе и комбинированных (коническо-цилиндрических, цилиндро-червячных и др.), выполняемых в виде самостоятельных агрегатов. Стандарт не распространяется на передачи редукторов специального назначения и специальной конструкции Для встроенных передач стандарт является рекомендуемым

Межосевые расстояния

1 ряд	40	50	63	80	100	125	—	160	—	200	—	250	—	315	—	400
2 ряд	—	—	—	—	—	—	140	—	180	—	225	—	280	—	355	—
1 ряд	—	500	—	630	—	800	—	1000	—	1250	—	1600	—	2000	—	2500
2 ряд	450	—	560	—	710	—	900	—	1120	—	1400	—	1800	—	2240	—

1-й ряд следует предпочитать 2-му

Межосевые расстояния для двухступенчатых несоосных редукторов общего назначения

Быстроходная ступень	40	50	63	80	100	125	140	160	180	200	225	250	280	315
Тихоходная ступень	63	80	100	125	160	200	225	250	280	315	355	400	450	500
Быстроходная ступень	355	400	450	500	560	630	710	800	900	1000	1120	1250	1400	1600
Тихоходная ступень	560	630	710	800	900	1000	1120	1250	1400	1600	1800	2000	2240	2500

Коэффициент запаса прочности при работе зуба двумя сторонами

Например: зубья реверсивных передач или зубья сателлитов в планетарных передачах

Материал колес и термо- обработка	Отливки стальные и чугунные без термо- обработки	Отливки стальные и чугунные с термо- обработкой	Поковки стальные нормали- зованные или улучшенные	Поковки и отливки стальные с поверх- ностной закалкой (сердцевина вязкая)	Стальные, нормали- зованные или улучшенные, а также с поверх- ностной закалкой	Стальные с объемной закалкой	Стальные, подверг- нутые цементации, азоти- рованию, циани- рованию и др.	Чугунные и пласт- массовые колеса
Коэфф.	1,9	1,7	1,5	2,2	1,4 — 1,6	1,8	1,2	1 — 1,2

Межосевые расстояния для трехступенчатых несоосных редукторов общего назначения

Быстроходная ступень	40	50	63	80	100	125	140	160	180	200
Промежуточная ступень	63	80	100	125	160	200	225	250	280	315
Тихоходная ступень	100	125	160	200	250	315	355	400	450	500
Быстроходная ступень	225	250	280	315	355	400	450	500	560	630
Промежуточная ступень	355	400	450	500	560	630	710	800	900	1000
Тихоходная ступень	560	630	710	800	900	1000	1120	1250	1400	1600

Номинальные передаточные числа

1 ряд	1,0	—	1,25	—	1,6	—	2,0	—	2,5	—	3,15
2 ряд	—	1,12	—	1,4	—	1,8	—	2,24	—	2,8	—
1 ряд	—	4,0	—	5,0	—	6,3	—	8,0	—	10	—	12,5
2 ряд	3,55	—	4,5	—	5,6	—	7,1	—	9,0	—	11,2	—

1-й ряд следует предпочитать 2-му Фактические значения передаточных чисел не должны отличаться от номинальных более чем на 2,5% при номинальном меньше 4,5 и на 4% при номинальном больше 4,5

Коэффициент ширины зубчатых колес (отношение ширины зубчатого колеса к межосевому расстоянию) должен соответствовать: 0,100; 0,125; 0,160; 0,200; 0,315; 0,400; 0,500; 0,630; 0,800; 1,0; 1,25

Численные значения ширины зубчатых колес округляются до ближайшего числа из ряда Ra20 по ГОСТу 6636.

При различной ширине сопряженных зубчатых колес значение коэффициента ширины зубчатых колес относится к более узкому из них.

Обозначение шлицевых эвольвентных соединений

Варианты условных обозначений эвольвентных шли­цевых соединений на чертежах показаны на рис 17.

Центрирование по боковым сторонам

Рисунок 17. Шлицевое эвольвентное соединение при центрировании по боковым сторонам зубьев.

Шлицевое эвольвентное соединение с D = 65мм; т = 3 мм, при центрировании по боковым сторонам зубьев с посадкой 9H/9g.

Центрирование по наружному диаметру:

Центрирование по внутреннему диаметру:

здесь: D=65, m=3, центрирование по внутреннему диаметру с посадкой H7/g6, посадки остальных поверхностей предусмотрены в табл.5.

Предельные значения радиального биения должны соответствовать значениям табл…., а ориентировочно это половина суммарного допуска

T ( т.е. Fr = 0,5 T ).

Пример выбора параметров эвольвентного шлицевого соединения.

Для подвижного шлицевого соединения D = 50 мм, с модулем т = 2 мм, без повышенных требований к соосности, выбрать геометрические параметры, определить предельные размеры вала и втулки, представить схему расположения полей допусков с оценкой предельных зазоров.

Принимаем центрирование шлицевого соединения по боковым поверхностям зубьев. По номинальному (исходному) диаметру соединения D = 50 мм и модулю т = 2 мм, по табл. 2 определяем число зубьев z = 24.

• Геометрические параметры получаем в соответствии с табл. 1,
• где:
• для вала толщина зуба по делительной окружности
• s =(π/2) m+2 Xm tgα,
• здесь смещение исходного контура будет:

Xm=0.5(D — m z -1.1 m)

Xm=0.5 · (50 — 2·24 -1.1·2) = -0,1мм

1. Теперь:
2. s =(3,1415/2) · 2+2· (-0,1) · 0,5773
3. s =3,1415+(-0,11547)=3,026мм
4. для шлицевой втулки ширина впадины по делительной окружно­сти
5. s=e=3,026мм
6. диаметр окружности вершин зубьев:
7. da =d-0,2m
8. da =50-0,2·2=49,6 мм.
9. диаметр окружности вершин зубьев втулки
10. Da = D – 2m
11. Da = 50 – 2·2 = 46мм.
12. Диаметр делительной окружности вычисляем
13. d = mz = 2·24 =48мм.

Принимаем плоскую форму дна впадины и согласно примечанию к табл. 4. определяем, диаметр окружности впадин вала

• df тах = D­- 2,2т = 50 — 2,2·2 = 45,6 мм
• Диаметр окружности впадины втулки будет
• Df = D = 50 мм.

Учитывая заказанную подвижность соединения выбираем посадки с зазорами. на каждый размер шлицевых деталей по табл.4.

Для центрирования по боковым сторонам предусмотрены предпочтительные посадки 9H/9h и 9H/9g,больший зазор у 9H/9g, её принимаем и получаем формулу соединения.

По таблице приложения 22 выписываем параметры, для шлицевой втулки c полем 9H при D = 50 мм, и модуля т = 2 мм, ES=+71, ESe=+26, EI=0, для шлицевого вала c с полем 9g: es=-11, ese=-37, ei=-82.

Для большего диаметра примем посадку H16/d9 по таблице 4. Параметры шлицевой втулки по Df=50 ,будут определены по таблицам приложения: EI=0, ES=+1600, шлицевого вала по da= 49,6,es=-80,ei=-142.

Для меньшего диаметра по табл. 4 принимаем посадку H11/h16 определяя характеристики по таблицам допусков и посадок, приложения. Параметры шлицевой втулки при Da=46, будут EI=0, ES=+160, шлицевого вала при df= 45,6, es=0, ei=-1600мкм,

По полученным значениям отклонений не трудно получить предельные размеры поверхностей соединения. Результаты удобно представить в виде таблицы табл.6. Подсчитываем предельные размеры и допуски, занося в таблицу.

Таблица 6. Результаты.

Параметр мм	Поле допуска	Предельные отклонения мкм	Предельные размеры мм	Допуск мм
ES (es)	ESe (ese)	EI (ei)	max	min
Шлицевый вал
s=3,026	9g	-11	-37	-82	2,989	2,944	0.045
da=49,6	d9	-80	—	-142	49,520	49,458	0,062
df=45,6	h16	—	-1600	45,6	44,0	1,6
Шлицевая втулка
e=3,026	9H	+71	+26	3,097	3,052	0,045
Df=50	H16	+1600	—	51,6	50,0	1,6
Da=46	H11	+160	—	46,16	46,0	0,16

Схемы расположения полей допусков изображены на рис.9.

1. Рисунок 18. Графическое представление посадок шлицевого соединения 65x3x 9H/9g Гост 6033-60
2. Определяем наибольший Smax и наименьший Smin зазоры для посадки 9H/9g по боковым поверхностям зубьев:
3. Smax =eimax — Smin = 3,097 — 2,944 = 0,153мм;
4. Smin =eimin — Smax = 3,052 — 2,989 =0,063 мм.



Геометрические параметры

Возведенные проекта грядущего колеса начинается с расчета его показателей.

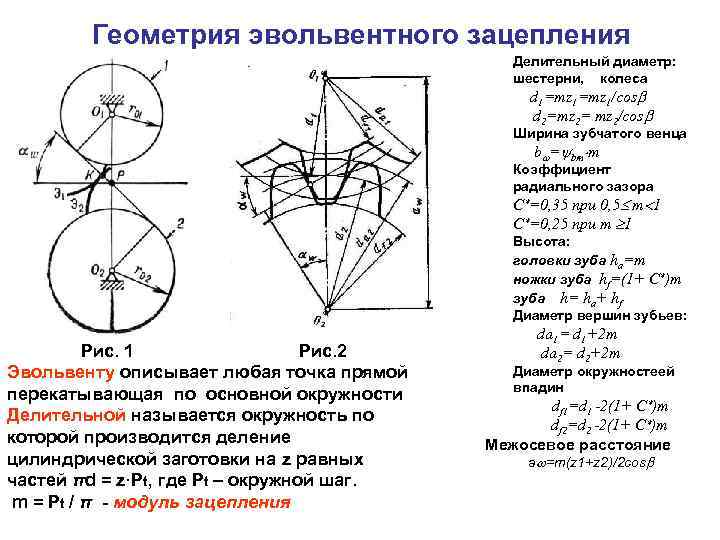
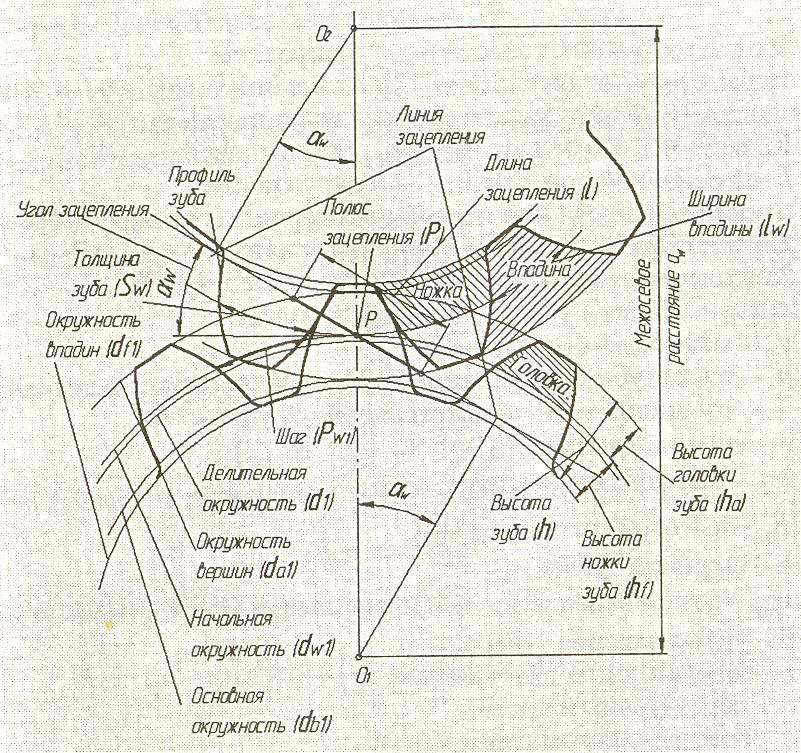
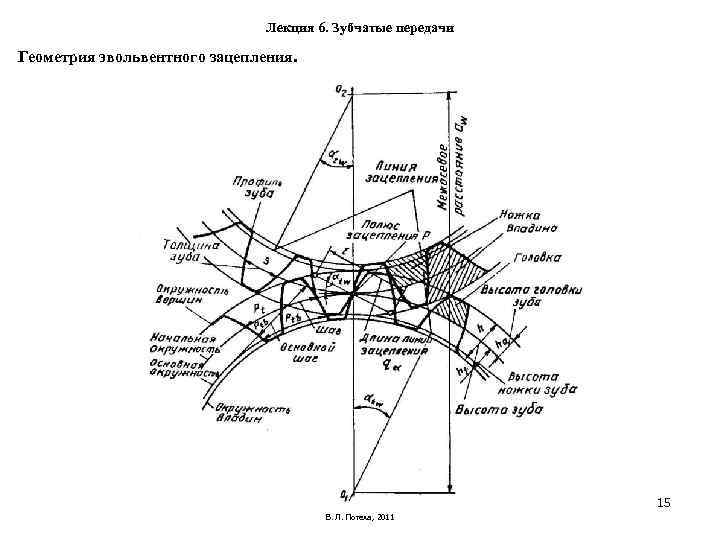
Рассмотрим параметры эвольвентного зацепления:

• шаг;
• модуль;
• число зубьев;
• угол профиля;
• показатель смещения.

Шаг бывает двух вариантов:

1. Окружной — длина между равнорасположенных точек на соседних зубьях.
2. Угловой – центральный угол, характеризрующий дугу делительной окружности.

Модуль — диаметр круга шестерни в миллиметрах, измеряемый к одному зубу. Разделяется на 3 вида: начальный (критерий окружности колеса начальной поверхности), ключевой и делительный (окружность колеса с классическими значениями модуля и шага).

Число зубьев может быть различное, и зависит от диаметра шестерни, параметров в техническом плане и параметров готового механизма. К их показателям можно отнести:

Угол профиля устанавливается между конкретной точкой зуба, которая лежит на делительной окружности шестерни и вектором, прочерченным к точке от центра круга.

Аналогичное сцепление применяется в самых разных сферах. Его легко повстречать в автомобилестроении (в коробках передач автомобилей, в строительной, военной, сельскохозтехнике, кораблестроении, гидравлических насосах, лебедках и часовых механизмах).

На данное время можно найти много разновидностей аналогичных шестерен, которые имеют разные свойства и геометрию. При подборе зубчатых колес сначала необходимо смотреть на крепость и шумовые характеристики

Акцентированного внимания просит твердость метала, что очень важно для правильной работы соответствующего механизма

Если вы нашли погрешность, пожалуйста, выдилите фрагмент текста и нажмите Ctrl+Enter.

Основные ошибки самостоятельной замены

Несмотря на предельно простую технологию, автолюбители часто допускают при замене венца следующие ошибки:

• перед тем, как снять зубчатый обод, следует произвести ревизию боковой плоскости маховика под сцепление, и отверстий для крепежных болтов;
• установка с перегревом отдельных участков венца приведет к быстрому износу зубьев именно на этих местах, так как происходит отпуск стали;
• наружный диаметр зубьев должен иметь фаску для плавного зацепления с бендиксом стартера без ударов.

Для того, чтобы уменьшить износ двигателя и увеличить приемистость машины на высоких оборотах, маховик часто облегчают. Из-за наличия дополнительных отверстий на наружном диаметре диска в зоне, примыкающей к зубчатому ободу, венец часто приваривается к диску.

Таким образом, венец можно заменить собственными силами при значительной выработке профиля зуба на отдельных участках. Снять обод можно на холодную, а при установке потребуется нагрев до 200 градусов максимум.

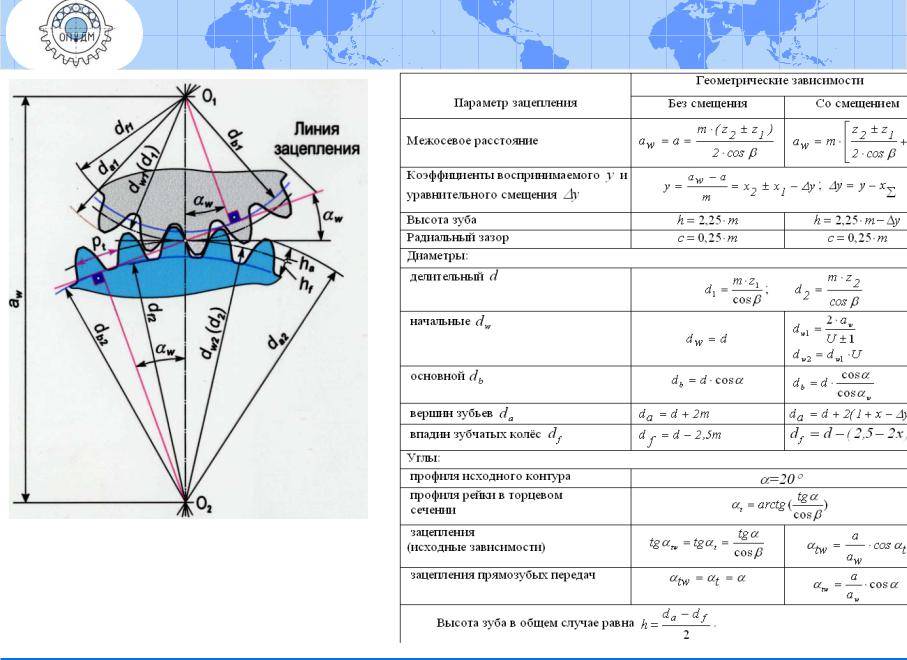
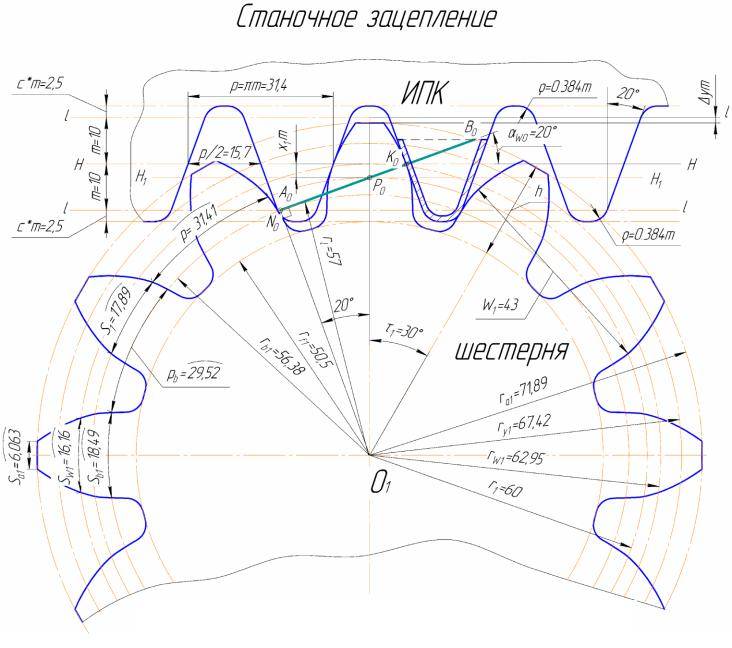
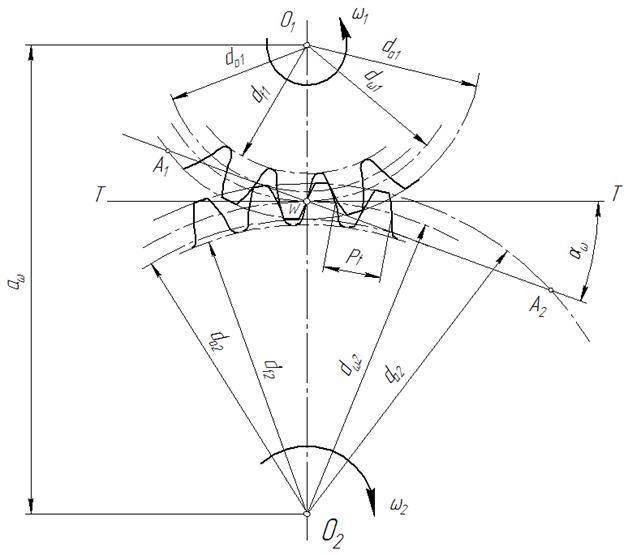
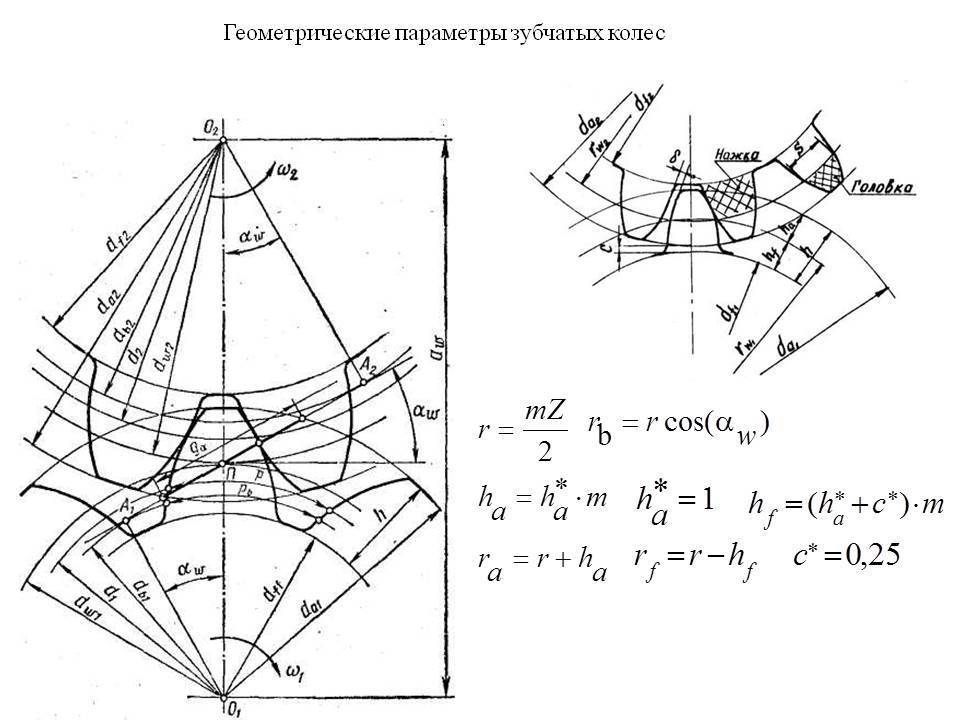
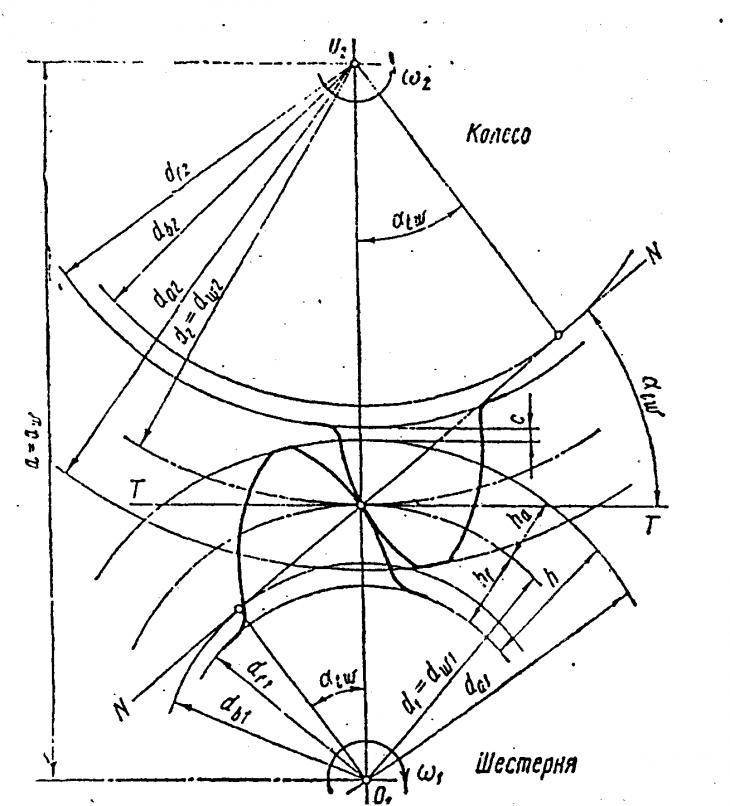
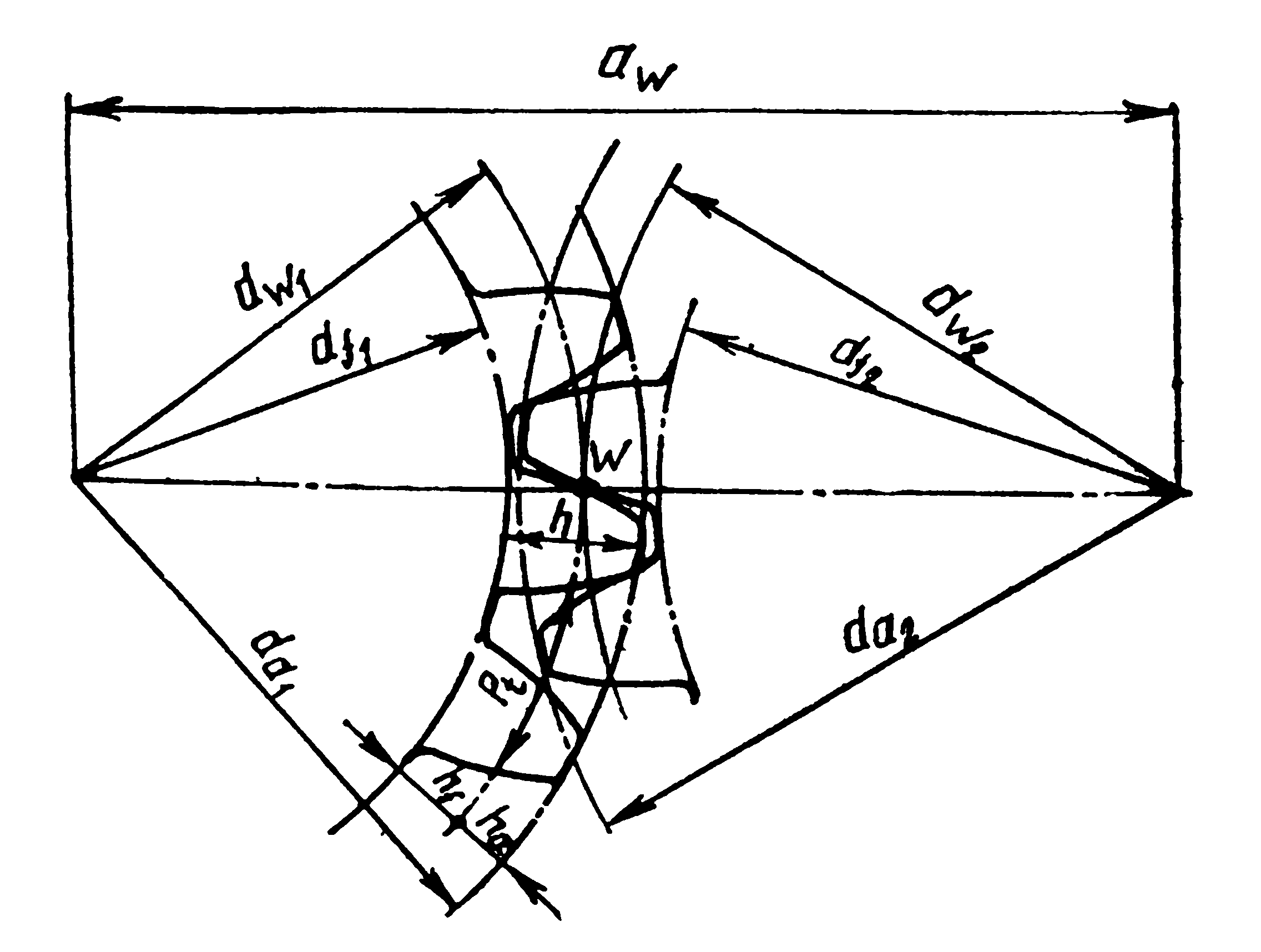
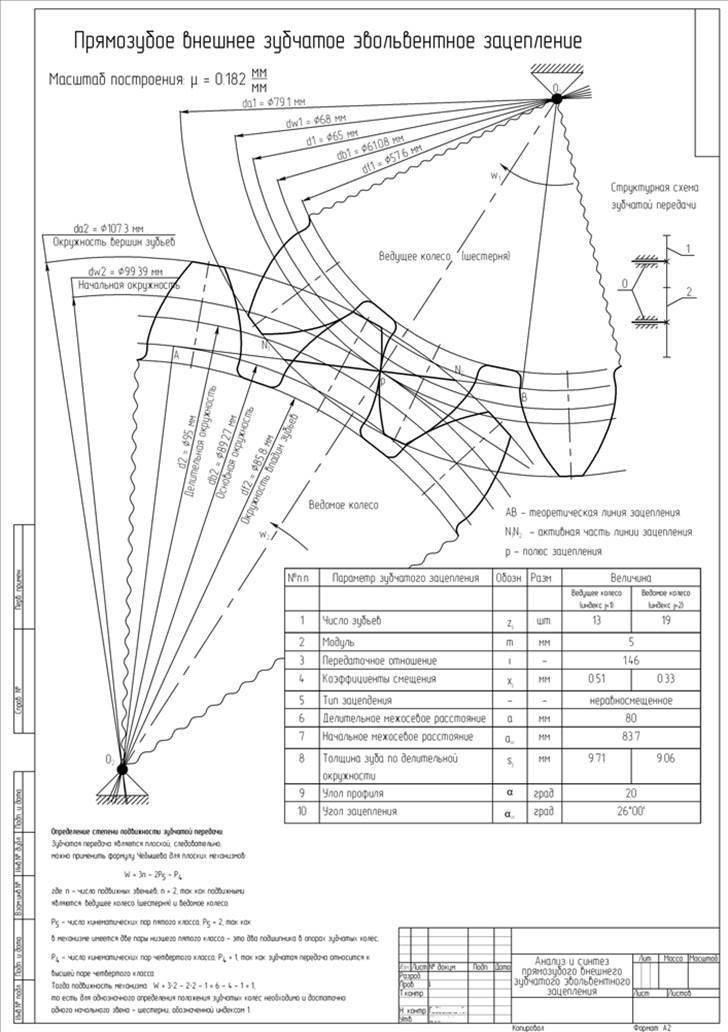
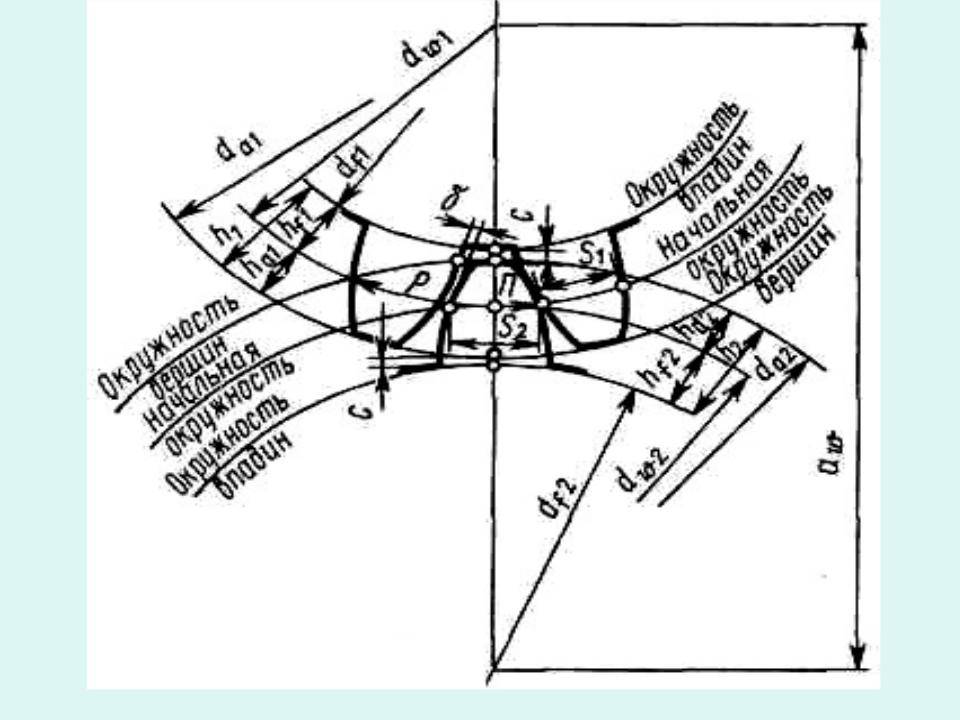
Геометрический расчет элементов цилиндрической зубчатой передачи

Исходные данные для расчета:

• Модуль m = 4 мм;
• Число зубьев шестерни Z1 = 18;
• Число зубьев колеса Z2 = 30;
• Диаметр вала (ведущий) DB1 = 22 мм;
• Тип шпонки – Призматическая;
• Число шлицев Z – 8;
• Внутренний диаметр шлицев d = 22 мм;
• Диаметр вала (ведомый) DB2 = 30 мм;
• Ширина шлица b = 6 мм;
• Тип – D.

Результаты геометрического расчета цилиндрической зубчатой передачи

• Делительный диаметр шестерни d1=mz1=4×18=72 мм;
• Делительный диаметр колеса d2=mz2=4×30=120 мм;
• Высота головки зуба ha=m =4 мм;
• Высота ножки зуба hf=1,25m=1,25×4=5 мм;
• Высота зуба h=ha+hf=2,25m=2,25×4=9 мм;
• Диаметр вершин зубьев шестерни da1=d1+2ha1=72+2×4=80 мм;
• Диаметр впадин шестерни df1=d1-2hf=72-2×5=62 мм;
• Длина ступицы шестерни Lст1=1,5DB1=1,5×22=33 мм;
• Наружный диаметр ступицы шестерни Dст1=1,6DB1=1,6×22=35,2 мм;
• Диаметр вала шестерни D1=1,2×22=26,4 мм;
• Делительный диаметр колеса d2=mz2=4×30=120 мм;
• Диаметр вершин зубьев колеса da2=d2+2ha=120+2×4=128 мм;
• Диаметр впадин колеса df2=d2-2hf2=120-2×5=110 мм;
• Длина ступицы колеса Lст2=1,5DB2=1,5×30=45 мм;
• Наружный диаметр ступицы колеса Dст2=1,6DB2=1,6×30=48 мм;
• Диаметр вала колеса D2=1,2DB2=1,2×30=36 мм;
• Ширина зубчатого венца b=6m=6×4=24 мм;
• Толщина обода зубчатого венца δ1=2,25m=2,25×4=9 мм;
• Толщина диска δ2=1/3b=8 мм;
• Межосевое расстояние a=0,5(d1+d2)=0,5(72+120)=96 мм;
• Длина шлицев Lшл=(1,5. 2)Lст2=(1,5. 2)45=72 мм.

Изготовление зубчатых колёс

Существует несколько  методов изготовления колес.

Метод обката

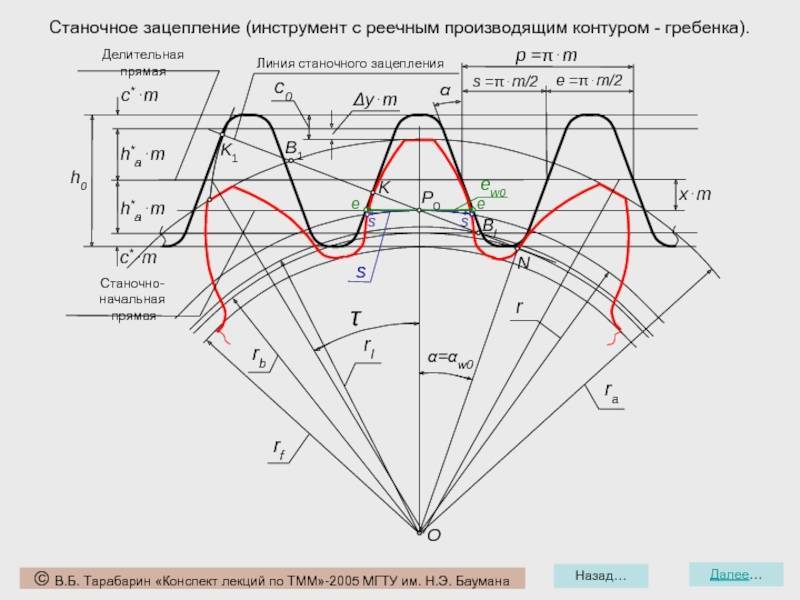
В настоящее время является наиболее технологичным, а поэтому и самым распространённым способом изготовления зубчатых колёс. При изготовлении зубчатых колёс могут применяться такие инструменты, как гребёнка, червячная фреза и долбяк.

Метод обката с применением гребёнки

Изготовление шестерни.
Изготовление зубчатого колеса.

Режущий инструмент, имеющий форму зубчатой рейки, называется гребёнкой. На одной стороне гребёнки по контуру её зубьев затачивается режущая кромка.

Заготовка накатываемого колеса совершает вращательное движение вокруг оси. Гребёнка совершает сложные перемещения, состоящие из поступательного движения перпендикулярно оси колеса и возвратно-поступательного движения (на анимации не показано), параллельного оси колеса для снятия стружки по всей ширине его обода. Относительное движение гребёнки и заготовки может быть и иным, например, заготовка может совершать прерывистое сложное движение обката, согласованное с движением резания гребёнки.

Заготовка и инструмент движутся на станке друг относительно друга так, как будто происходит зацепление профиля нарезаемых зубьев с исходным производящим контуром гребёнки.

Метод обката с применением червячной фрезы

Помимо гребёнки в качестве режущего инструмента применяют червячную фрезу. В этом случае между заготовкой и фрезой происходит червячное зацепление.

Метод обката с применением долбяка

Зубчатые колёса также долбят на зубодолбёжных станках с применением специальных долбяков.

Зубодолбёжный долбяк представляет собой зубчатое колесо, снабжённое режущими кромками. Поскольку срезать сразу весь слой металла обычно невозможно, обработка производится в несколько этапов.

При обработке инструмент совершает возвратно-поступательное движение относительно заготовки. После каждого двойного хода, заготовка и инструмент поворачиваются относительно своих осей на один шаг. Таким образом, инструмент и заготовка как бы «обкатываются» друг по другу. После того, как заготовка сделает полный оборот, долбяк совершает движение подачи к заготовке. Этот процесс происходит до тех пор, пока не будет удалён весь необходимый слой металла.

Литейная форма для бронзового храпового колеса (Китай, династия Хань. (206 до н. э. — 220 н. э.)).

Метод копирования (Метод деления)

Дисковой или пальцевой фрезой нарезается одна впадина зубчатого колеса. Режущая кромка инструмента имеет форму этой впадины. После нарезания одной впадины заготовка поворачивается на один угловой шаг при помощи делительного устройства, операция резания повторяется.

Метод применялся в начале XX века. Недостаток метода состоит в низкой точности: впадины изготовленного таким методом колеса сильно отличаются друг от друга.

Горячее и холодное накатывание

Процесс основан на последовательной деформации нагретого до пластического состояния слоя определенной глубины заготовки зубонакатным инструментом. При этом сочетаются индукционный нагрев поверхностного слоя заготовки на определенную глубину, пластическая деформация нагретого слоя заготовки для образования зубьев и обкатка образованных зубьев для получения заданной формы и точности.

Изготовление конических колёс

Технология изготовления конических колёс теснейшим образом связана с геометрией боковых поверхностей и профилей зубьев.

Способ копирования фасонного профиля инструмента для образования профиля на коническом колесе не может быть использован, так как размеры впадины конического колеса изменяются по мере приближения к вершине конуса. В связи с этим такие инструменты, как модульная дисковая фреза, пальцевая фреза, фасонный шлифовальный круг, можно использовать только для черновой прорезки впадин или для образования впадин колёс не выше восьмой степени точности.

Для нарезания более точных конических колёс используют способ обкатки в станочном зацеплении нарезаемой заготовки с воображаемым производящим колесом. Боковые поверхности производящего колеса образуются за счёт движения режущих кромок инструмента в процессе главного движения резания, обеспечивающего срезание припуска. Преимущественное распространение получили инструменты с прямолинейным лезвием. При прямолинейном главном движении прямолинейное лезвие образует плоскую производящую поверхность. Такая поверхность не может образовать эвольвентную коническую поверхность со сферическими эвольвентными профилями. Получаемые сопряжённые конические поверхности, отличающиеся от эвольвентных поверхностей, называют квазиэвольвентными.

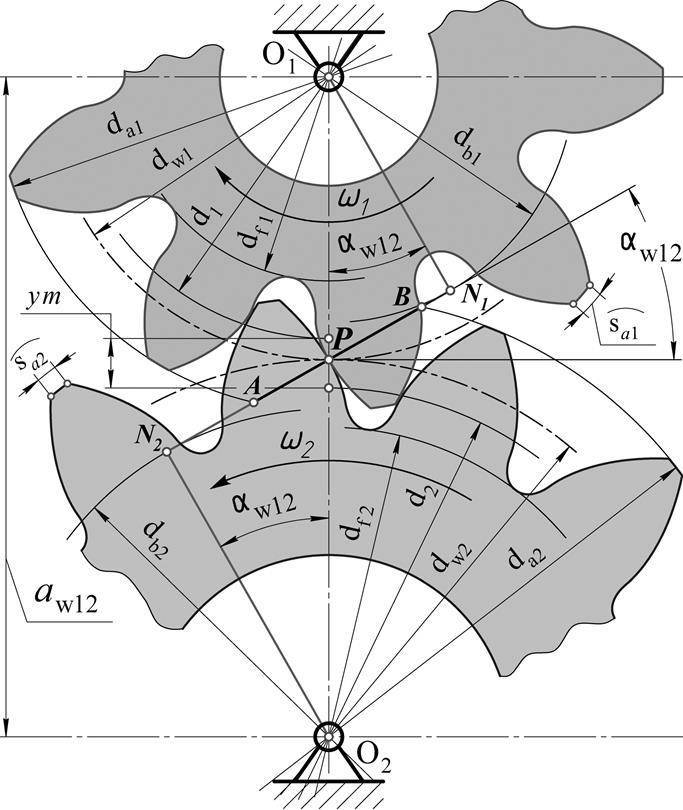
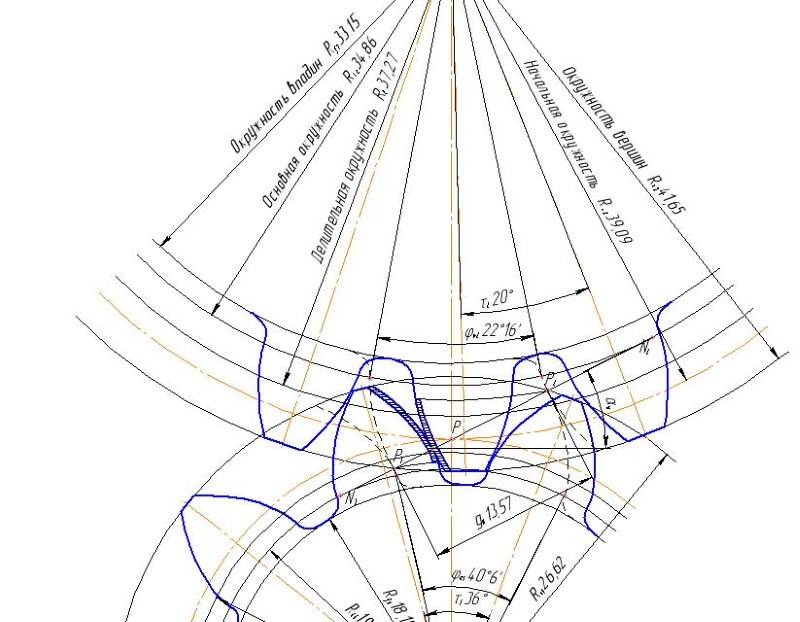
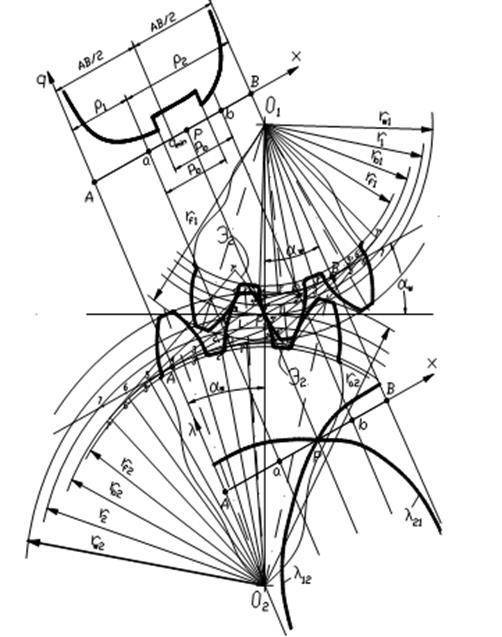
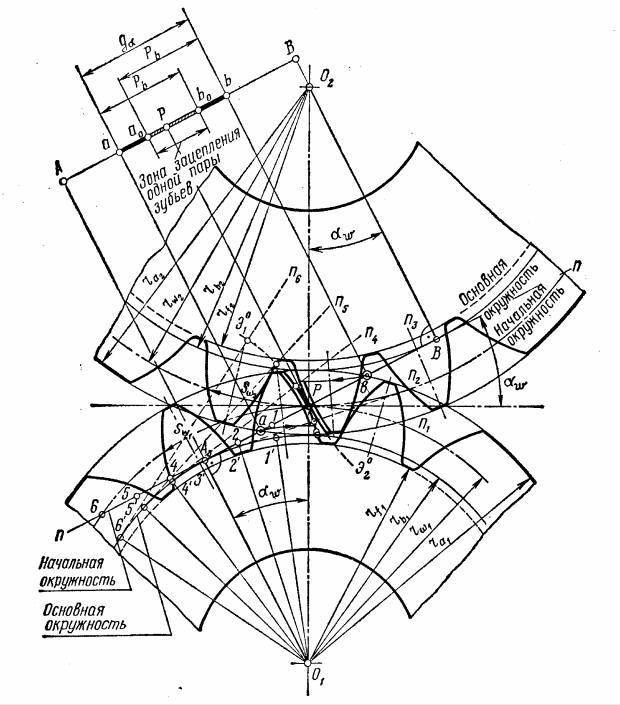
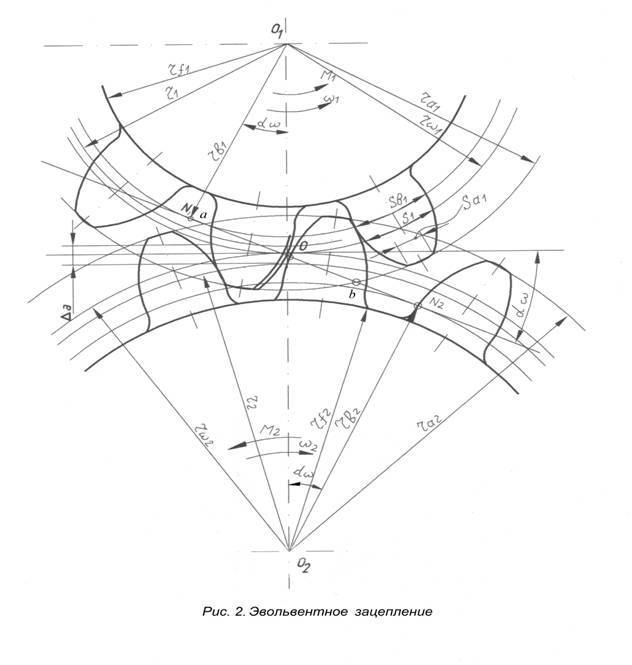
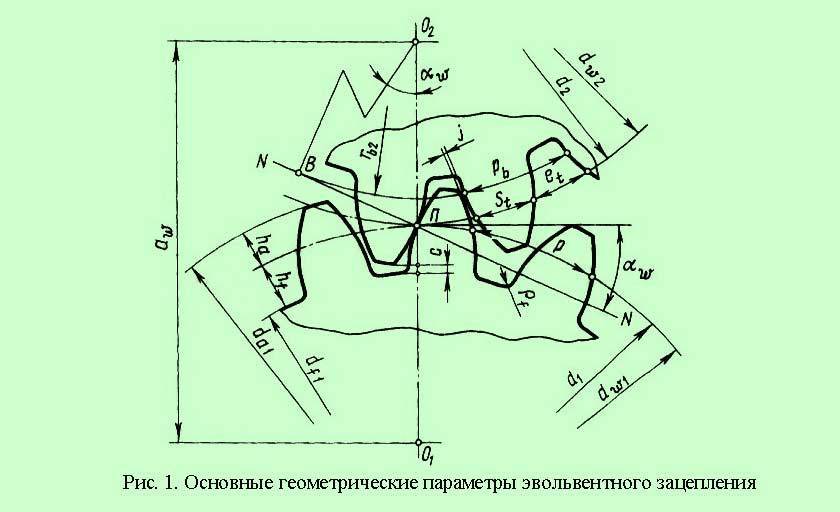
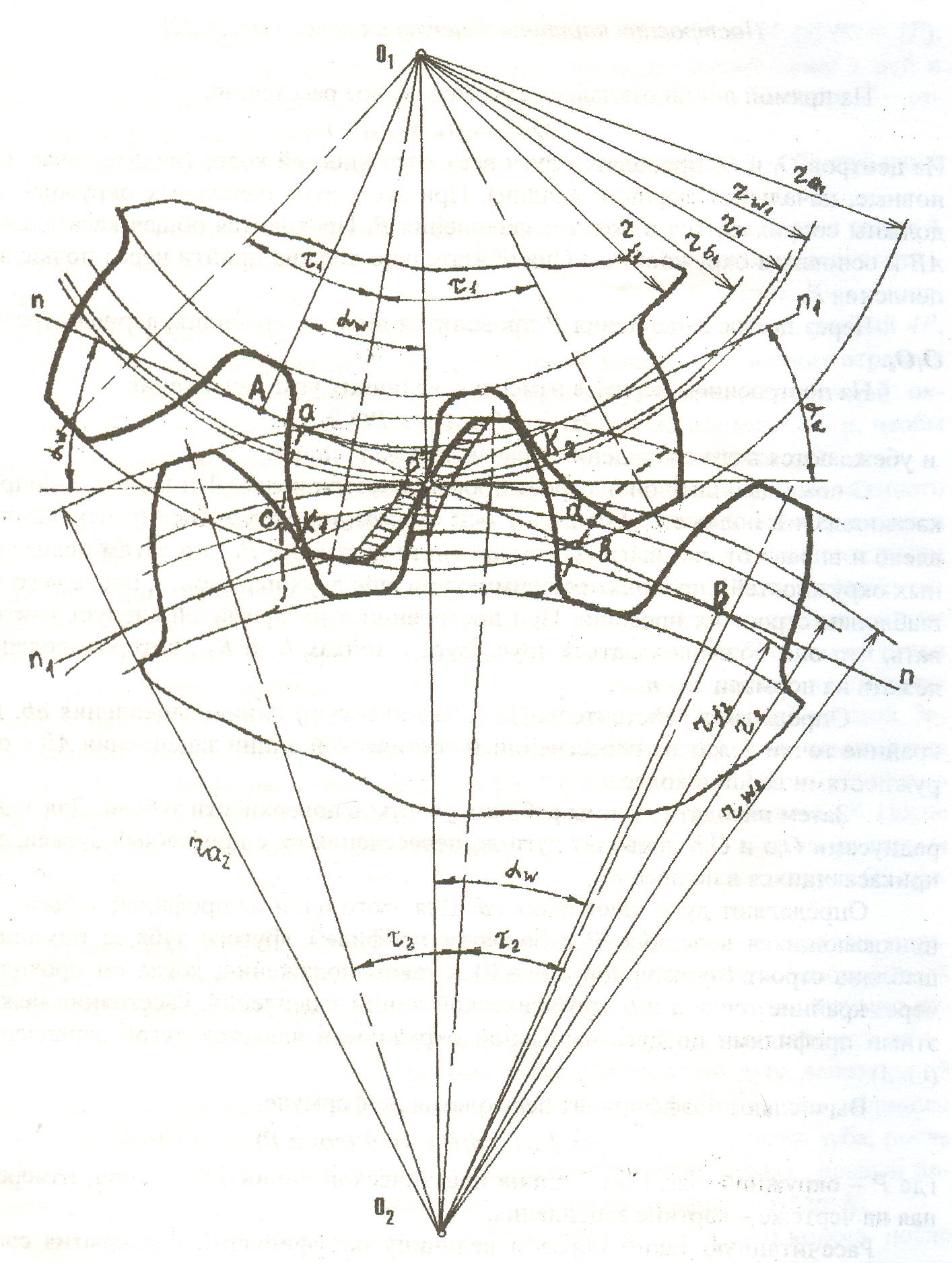
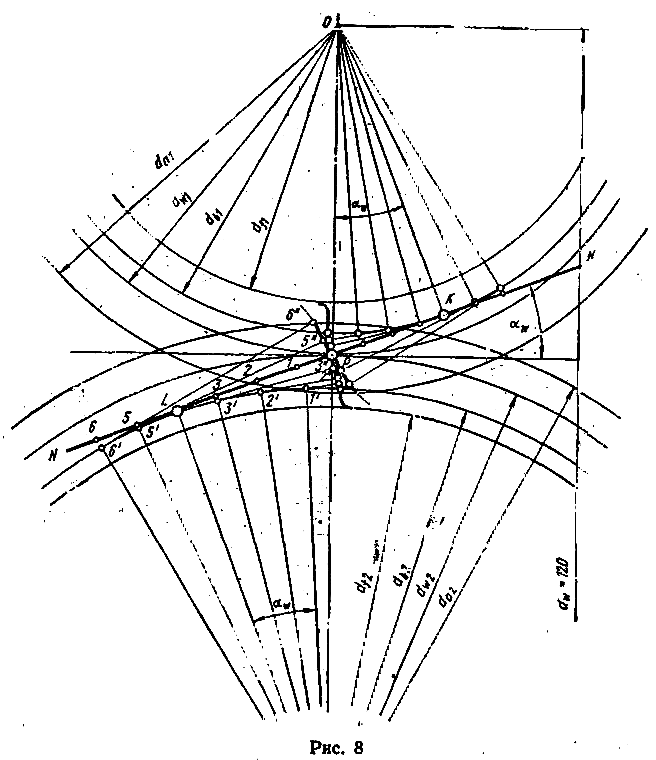
Построение эвольвентного зацепления

Способ приближённого построения эвольвентного зубчатого зацепления. Подходит для технических рисунков, построенных от руки или с помощью САПР.

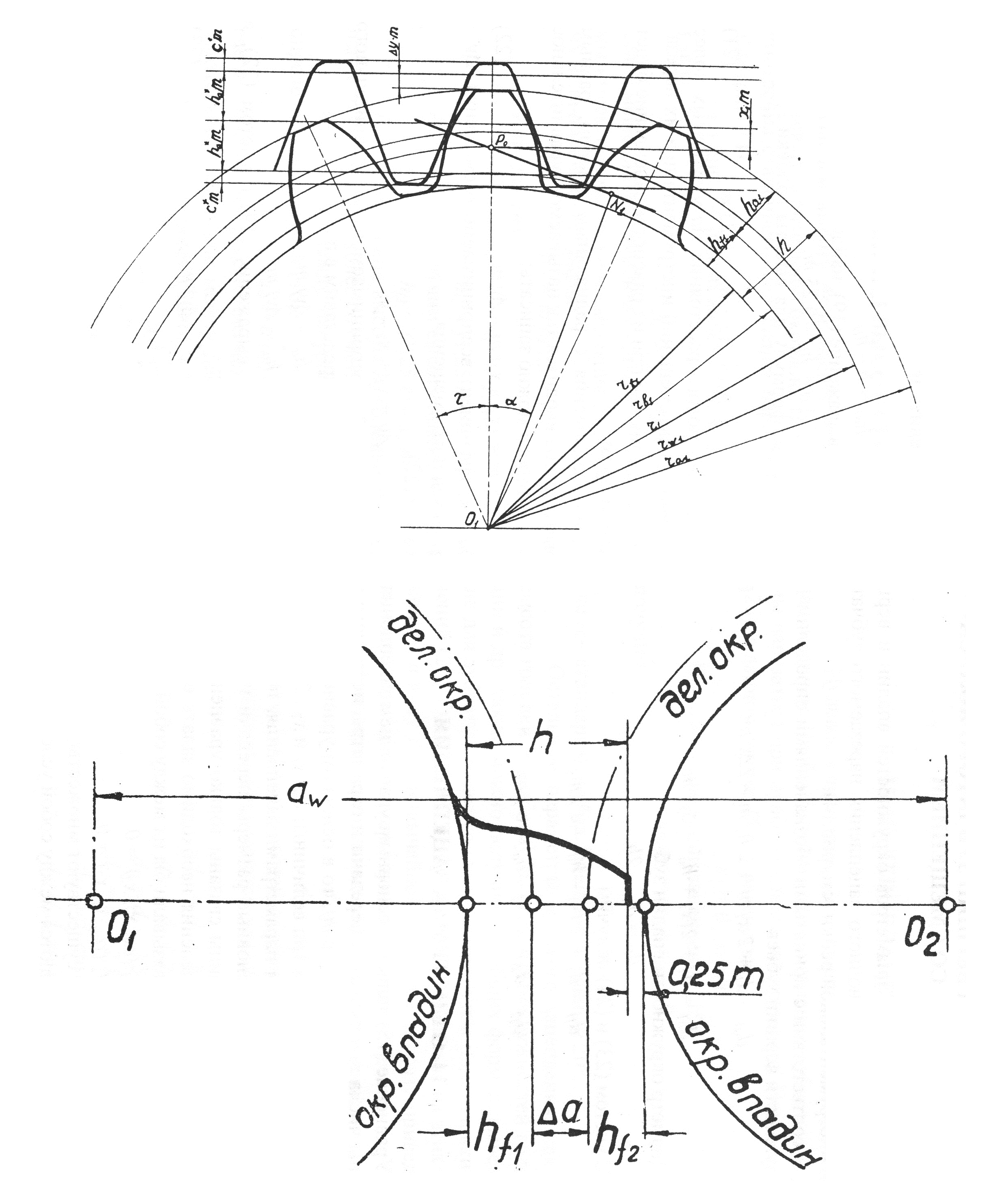
Перед построением необходимо задать следующие размеры:

• высота ножки зуба hf{\displaystyle h_{f}} (на рис. обозначена a);
• высота головки зуба ha{\displaystyle h_{a}} (на рис. обозначена b);
• диаметр начальной окружности dw{\displaystyle d_{w}} (на рис. обозначен D);
• угол зацепления α{\displaystyle \alpha } (на рис. обозначен φ);
• окружная толщина зуба s_t;
• радиус кривизны переходной кривой в граничной точке профиля ρ_f.

	Изобразите начальную окружность (pitch circle) с диаметром D, и центром шестерни O. Окружность показана красным цветом. Изобразите окружность вершин зубьев (outside diameter) с центром в точке O с радиусом большим на высоту головки зуба(зелёного цвета). Изобразите окружность впадин зубьев (root diameter) с центром в точке O с радиусом меньшим на высоту ножки зуба (голубого цвета).
	Проведите касательную к начальной окружности (розовая). В точке касания под углом φ проведите линию зацепления (line of action), оранжевого цвета. Изобразите окружность, касательную к линии зацепления, с центром в точке O. Эта окружность является основной (base circle) и показана синим цветом.
	Отметьте точку A на окружности вершин зубьев. На прямой соединяющие точки A и O отметьте точку B находящуюся на основной окружности. Разделите расстояние AB на 3 части и отметьте точкой C полученное значение от точки A в сторону точки B на отрезке AB.
	От точки C проведите касательную к основной окружности. В точке касания отметьте точку D. Разделите расстояние DC на четыре части и отметьте точкой E полученное значение от точки D в сторону точки C на отрезке DC.
	Изобразите дугу окружности с центром в точке E, что проходит через точку C. Это будет часть одной стороны зуба (показана оранжевым цветом). Изобразите дугу окружности с центром в точке C и радиусом, равным толщине зуба. Место пересечения с начальной окружностью (pitch circle) отметьте точкой F. Эта точка находится на другой стороне зуба.
	Изобразите скругление (fillet) между стороною зуба и окружностью впадин зубьев (root diameter). Изобразите радиус профиля зуба — дугу окружности радиусом EC из точки F (отмечено темно зеленым). Отметьте место пересечения радиуса профиля зуба с основной окружностью точкой G (точка G на изображении показана не верно)
	Изобразите радиус профиля зуба — дугу окружности радиусом EC из точки G — это другая сторона зуба. Добавьте скругление у основания зуба к окружности впадин зубьев (как в предыдущем шаге)
	Зуб готов. Наружная окружность между двумя боковыми поверхностями – это вершина зуба. Повторите операцию для каждого зуба.

Перед построением эвольвентного зацепления необходимо рассчитать его геометрические параметры. Предположим, что даны числа зубьев колеса z1{\displaystyle z_{1}} и шестерни z2{\displaystyle z_{2}}, указан тип зацепления: нулевое, равносмещенное или неравносмещенное. Сначала исходя из типа по таблицам или блокирующему контуру нужно выбрать коэффициенты смещения x1{\displaystyle x_{1}} и x2{\displaystyle x_{2}}.

Определение усилий в кинематических парах

. На первом этапе вычисляем значения равнодействующих систем сил:

.
Вычерчиваем наиболее удаленную группу Ассура (звенья 5 и 4), с сохранением всех
геометрических размеров.

На
группу Ассура начерченную дополнительно помимо сил реакции связей наносят
направления линейных ускорений центров масс, угловых ускорений и
равнодействующих соответствующих систем сил используя план ускорений. Сила P₅₄ – действие звена 5 на звено 4, P₃₄ – действие звена 3 на звено 4.

Выполнив
выше описанное, записываем уравнение моментов для 4-ого и 5-ого звеньев
относительно точки С, используя теорему Вариньона:

Так как используется графический метод для решения последнего уравнения
необходимо ввести масштаб сил

Строем план сил и находим неизвестные величины:

4. Рассмотрим звенья 3 и 2. Вычерчиваем группу Ассура с сохранением всех
геометрических размеров.

На группу Ассура начерченную дополнительно помимо сил реакции связей
наносят направления линейных ускорений центров масс, угловых ускорений и
равнодействующих соответствующих систем сил используя план ускорений. Cила Р₄₃ – действие звена 3
на звено 4, сила P₃₂ – действие звена 2 на звено 3.
Записываем уравнение моментов для 2го звена относительно точки A, используя теорему Вариньона:

|

Так как используется графический метод для решения последнего уравнения
необходимо ввести масштаб сил К=279 Н/мм

Строем
план сил и находим неизвестные величины:

. Рассмотрим кривошип 1, для чего вычертим его с сохранением
геометрических размеров. P₂₁ – давление шатуна 2 на кривошип 1,
так как центр масс лежит на оси вращения О (кривошип уравновешен), то уравнение
сил будет иметь вид:

Выполнив второй лист курсового проекта произвел исследование
шарнирно-рычажного механизма. Выполнил кинематический и динамический анализ
механизма, графическим методом при помощи плана скоростей, ускорений и сил,
нашёл соответственно скорости, ускорения точек механизма и возникающие в
кинематических парах усилия.

Исследование кривошипно-ползунного механизма

Исходные данные

lOA=	0.1 м
lAB=	0.45 м
lAS2=	0.15 м
n*=	700 об/мин
KL=	0.002 м/мм
Ki=	15000 Па/мм
D=	0.15 м
d=	0.0 м
m2=	3.84кг
m3=	5.0 кг
=0.00625

Заключение

Данный курсовой проект по теории машин и механизмов является первой
самостоятельной расчетно-графической работой в процессе обучения в
университете. Он научил нас самостоятельно решать инженерные задачи, связанные
с анализом и синтезом механизмов.

В графической части проекта были спроектированы три механизма: зубчатый
механизм, где производилось исследование эвольвентного зацепления зубьев и
проектирование зубчатой передачи из условия получения наименьших её габаритов и
определение некоторых характеристик этой передачи; шарнирно – рычажный
механизм, где производился кинематический и динамический анализ конкретного
плоского шарнирно-рычажного механизма и кривошипно-ползунный механизм, для
которого были построены графики скорости и ускорения поршня, силы давления на
поршень, силы действующей на палец шатуна и моментов, действующих на кривошип.

В расчетно-пояснительной записке был произведен расчет характеристик
обоих механизмов. В исследовании эвольвентного зацепления зубьев мы нашли
наименьшее число зубьев и определили скорости скольжения зубьев. В исследовании
шарнирно-рычажного механизма мы определили скорости, угловые скорости,
ускорения, угловые ускорения звеньев механизма и усилия в кинематических парах.

В целом нами была произведена объемная работа, и знания, полученные нами
в ходе её выполнения, пригодятся в процессе дальнейшего обучения в
университете.

Список
литературы

. Исследование шарнирно-рычажных механизмов: Метод. Указания
к курсовому проектированию / Казан. гос. технол. ун-т; Сост.: Б.В. Крапоткин,
А.Г. Замалиев. Казань 2008. – 52 с.

. Методические указания к выполнению первого раздела
курсового проекта «Исследование эвольвентного зацепления» / Казан. гос. технол.
ун-т; Сост.: Б.В. Крапоткин, А.Г. Замалиев. Казань 1987. – 20 с.

. Артоболевский И.И. теория машин и механизмов: Учеб. Для
втузов. – 4-е изд., перераб. И доп. – М.: Наука, 2005. – 640 с.