Шкала измерений

Использование в психометрии

Основная статья: Психометрия

Используя различные шкалы, можно производить различные психологические измерения. Самые первые методы психологических измерений были разработаны в психофизике. Основной задачей психофизиков являлось то, каким образом определить, как соотносятся физические параметры стимуляции и соответствующие им субъективные оценки ощущений. Зная эту связь, можно понять, какое ощущение соответствует тому или иному признаку. Психофизическая функция устанавливает связь между числовым значением шкалы физического измерения стимула и числовым значением психологической или субъективной реакцией на этот стимул.

Свойства шкал

Неравномерная шкала омметра

• Начальное значение шкалы — наименьшее значение измеряемой величины, которое может быть отсчитано по шкале средства измерений. Во многих случаях шкала начинается с нулевой отметки, однако могут быть и другие значения — например, у медицинского термометра это 34,3 °C.
• Конечное значение шкалы — наибольшее значение измеряемой величины, которое может быть отсчитано по шкале средства измерений.
• Характер шкалы — функциональная зависимость a = f(x) между линейным (или угловым) расстоянием a какой-либо отметки от начальной отметки шкалы, выраженным в долях всей длины шкалы, и значением x измеряемой величины, соответствующим этой отметке:
  • Равномерная шкала — шкала, отметки на которой нанесены равномерно.
  • Неравномерная шкала — шкала, отметки на которой нанесены неравномерно.
  • Логарифмическая или гиперболическая шкала — шкала с сужающимися делениями, характеризуемыми тем, что отметка, соответствующая полусумме начального и конечного значений, расположена между 65 и 100 % длины шкалы. Следует заметить, что выражение «логарифмическая шкала» используется и по отношению к другому значению понятия «шкала» (см.: Шкала физической величины, Логарифмический масштаб).
  • Степенная шкала — шкала с расширяющимися или сужающимися делениями, но не подпадающая под определение логарифмической (гиперболической) шкалы.

Шкала интервалов (разностей)

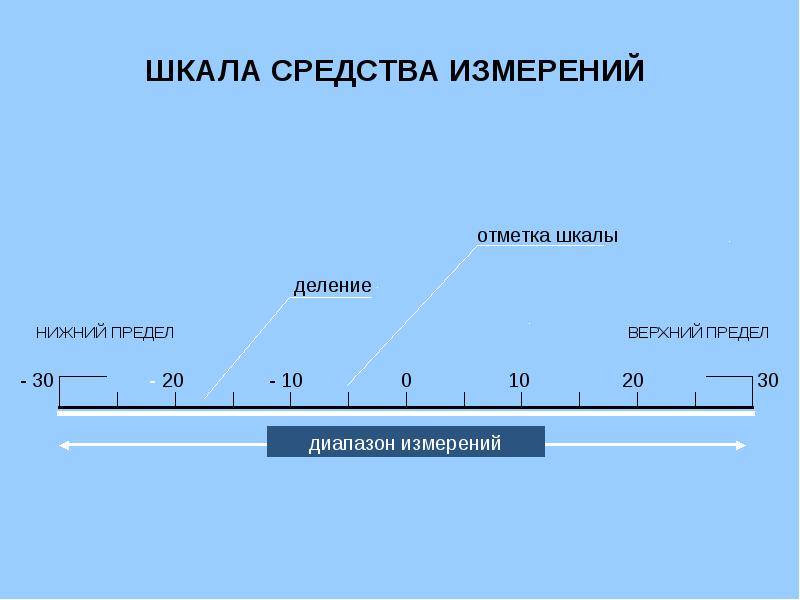
Эти шкалы измерений в метрологии являются дальнейшим развитием шкал порядка и применяются для объектов, свойства которых удовлетворяют отношениям эквивалентности, порядка и аддитивности. Шкала интервалов состоит из одинаковых интервалов, имеет единицу измерения и произвольно выбранное начало – нулевую точку. Пример шкалы интервалов — летоисчисление по различным календарям, в которых за начало отсчета принято либо сотворение мира, либо рождество Христово и т.д. Температурные шкалы Цельсия, Фаренгейта и Реомюра также являются шкалами интервалов.

Рисунок – Пример шкалы интервалов (Температурные шкалы Цельсия и Фаренгейта)

На шкале интервалов определены действия сложения и вычитания интервалов. Действительно, по шкале времени интервалы можно суммировать или вычитать и сравнивать, во сколько раз один интервал больше другого, но складывать даты каких-либо событий просто бессмысленно.

Шкала интервалов величины Q описывается уравнением Q = Qо + q, где q — числовое значение величины; Qо — начало отсчета шкалы;  — единица рассматриваемой величины. Такая шкала полностью определяется заданием начала отсчета Qо шкалы и единицы данной величины .

Задать шкалу практически можно двумя путями. При первом из них выбираются два значения Qо и Q1, величины, которые относительно просто реализованы физически. Эти значения называются опорными точками, или основными реперами, а интервал (Q1 ~ Qо) — основным интервалом. Точка Qо принимается за начало отсчета, а величина (Q1 -Qо)/n= за единицу Q. При этом n выбирается таким, чтобы было целой величиной.

Рисунок – Пример шкалы отношений

При втором пути задания шкалы единица воспроизводится непосредственно как интервал, его некоторая доля или некоторое число интервалов размеров данной величины, а начало отсчета выбирают каждый раз по-разному в зависимости от конкретных условий изучаемого явления. Пример такого подхода — шкала времени, в которой 1с = 9192631770 периодов излучения, соответствующих переходу между двумя сверхтонкими уровнями основного состояния атома цезия-133. За начало отсчета принимается начало изучаемого явления.

Шкала отношений

Шкала отношений описывает свойства эмпирических объектов, которые удовлетворяют отношениям эквивалентности, порядка и аддитивности (шкалы второго рода — аддитивные), а в ряде случаев и пропорциональности (шкалы первого рода — пропорциональные). Пример шкалы отношений — шкала массы (второго рода), термодинамической температуры (первого рода).

В шкалах отношений существует однозначный естественный критерий нулевого количественного проявления свойства и единица измерений, установленная по соглашению. С формальной точки зрения этот вид шкал измерений является шкалой интервалов с естественным началом отсчета

К значениям, полученным по этой шкале, применимы все арифметические действия, что имеет важное значение при измерений физических величин

Рисунок – Пример абсолютной шкалы (шкала температур Кельвина)

Шкалы отношений — самые совершенные. Они описываются уравнением Q = q, где Q — ФВ, для которой строится шкала, — ее единица измерения, q — числовое значение ФВ. Переход от одной шкалы отношений к другой происходит в соответствии с уравнением q2 = q1/.

Шкалы и их классификации

Шкалы используются как для первичных измерений, так и для перевода разных измерений (в нашем случае — различных показателей) в единую шкалу. Как выбрать единую шкалу? Начнём с трёх определений.

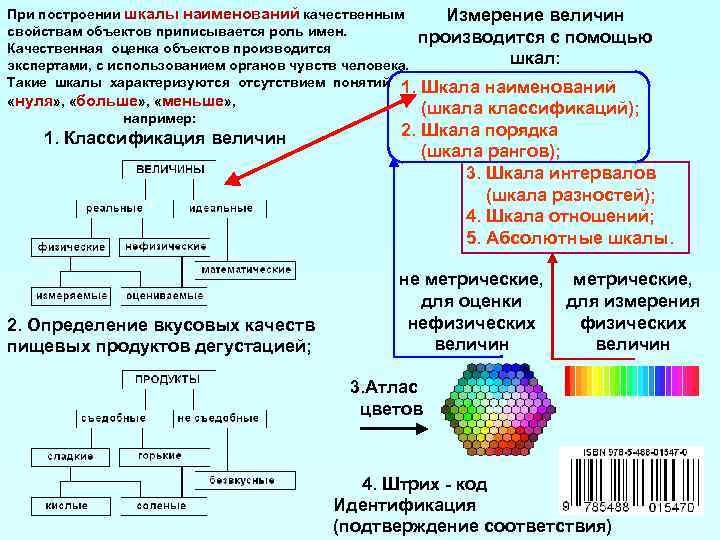
Шкалой называют систему чисел или иных элементов и отношений между ними, принятых для измерения или оценки каких-либо величин (объектов, качеств и т. д.).

Шкалирование — это:

• выбор шкалы для первичных измерений;
• перевод измерения из одной шкалы в другую.

Нормирование (или единообразное шкалирование) — это перевод всех переменных, показателей, отражающих разные объекты измерений, в одну шкалу.

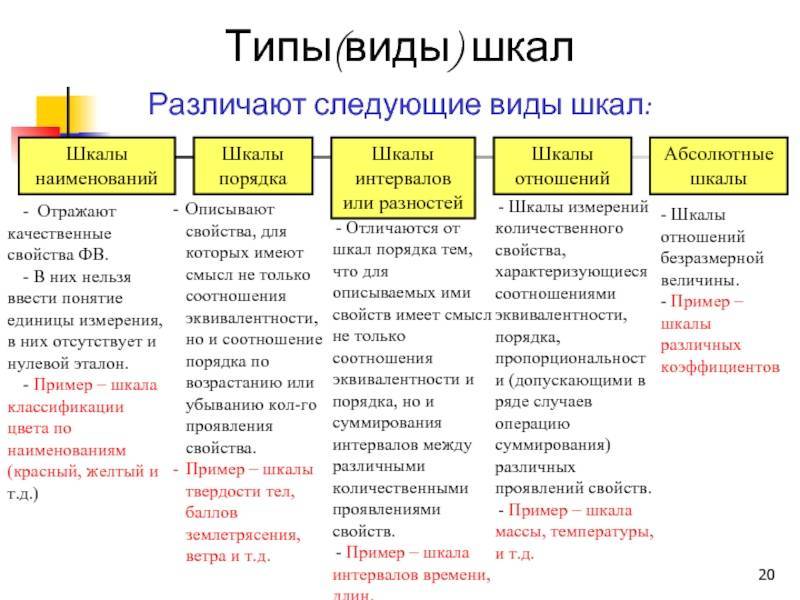
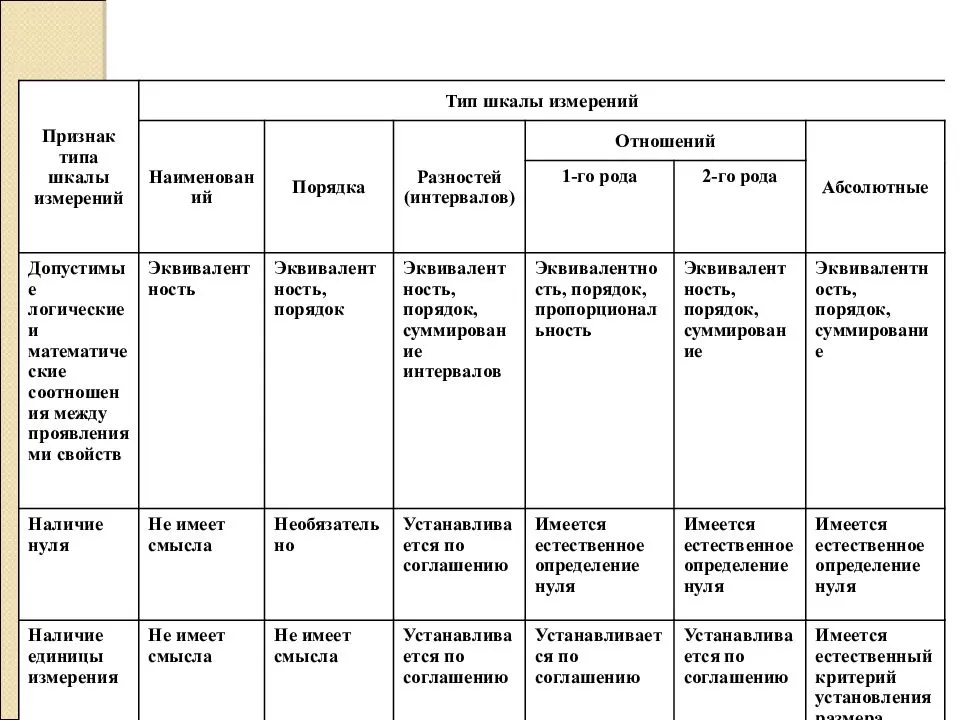
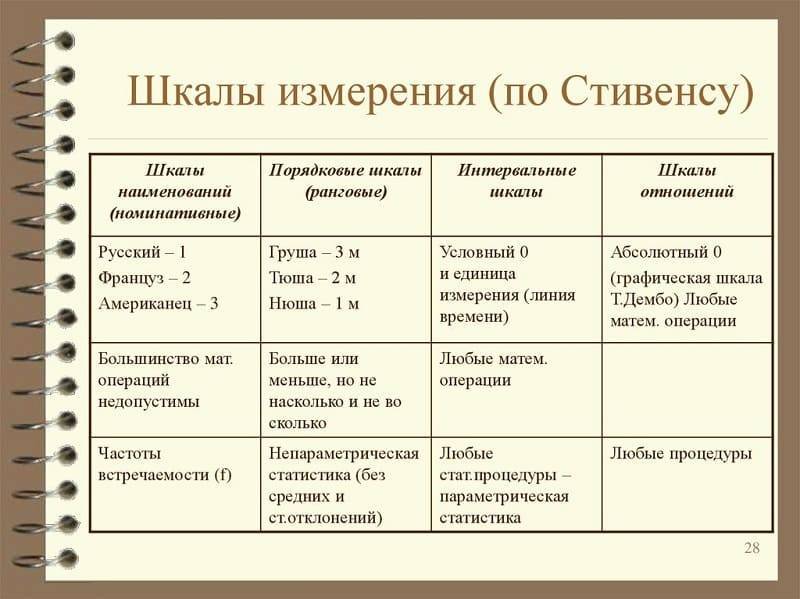
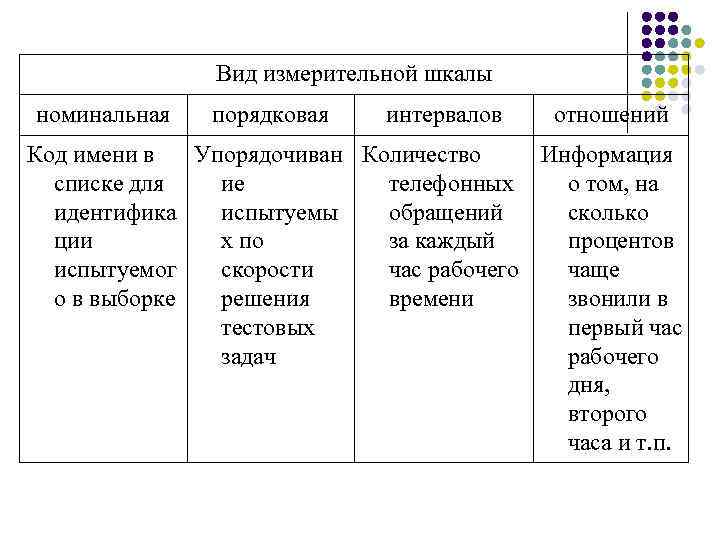
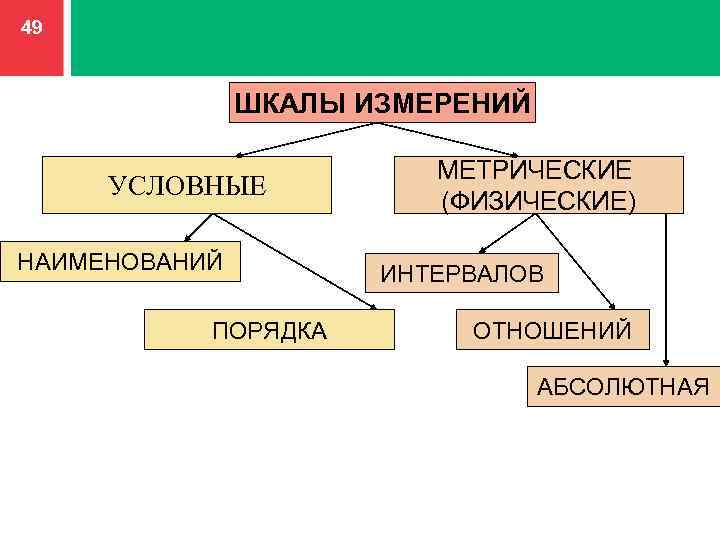
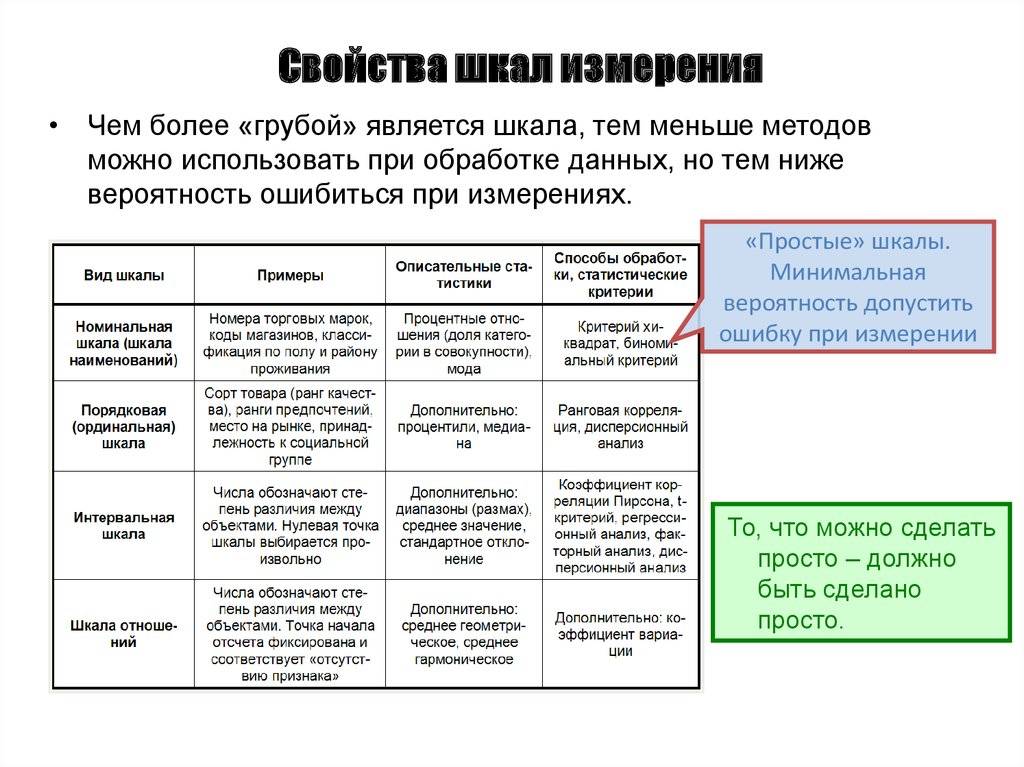
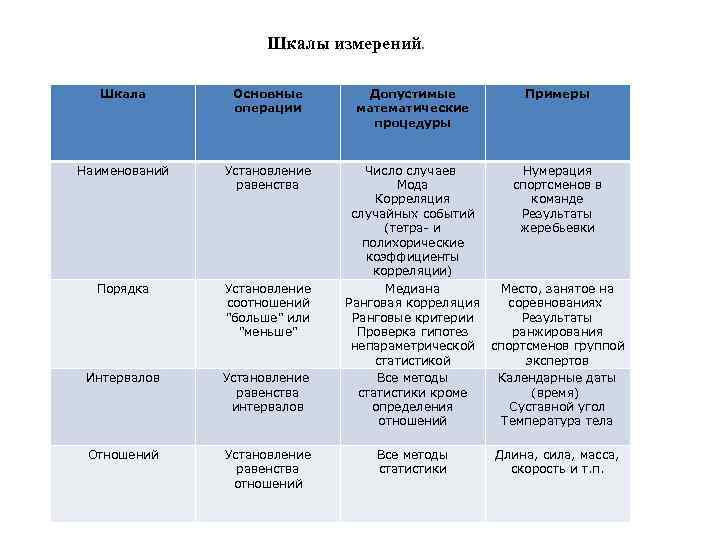
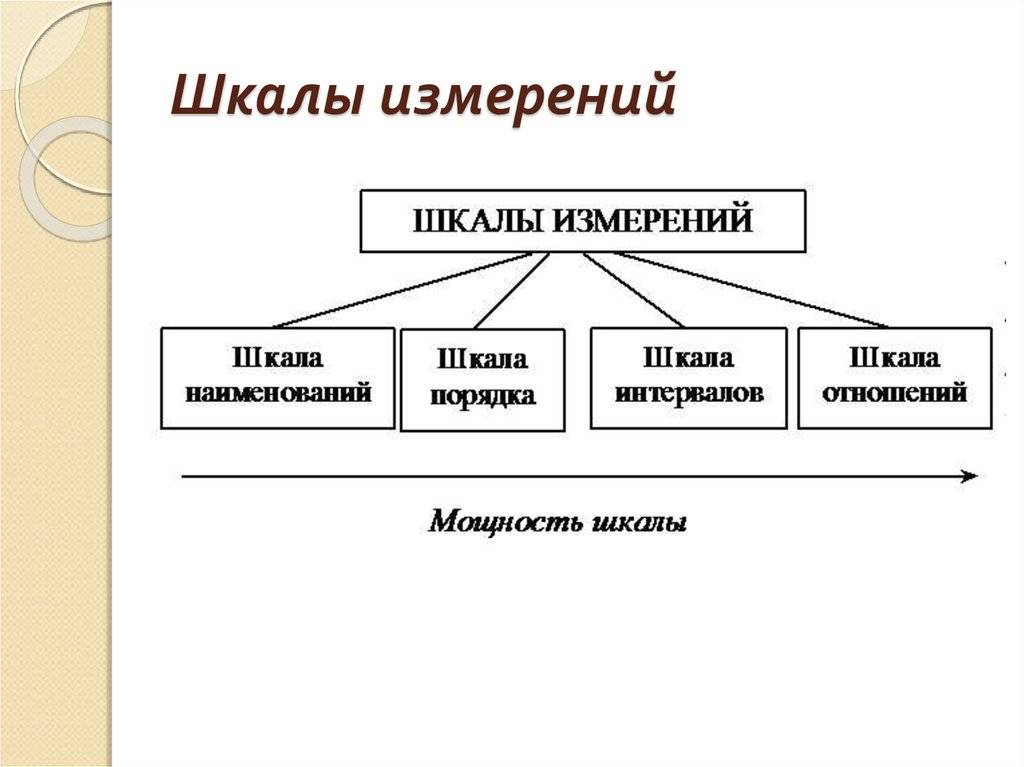
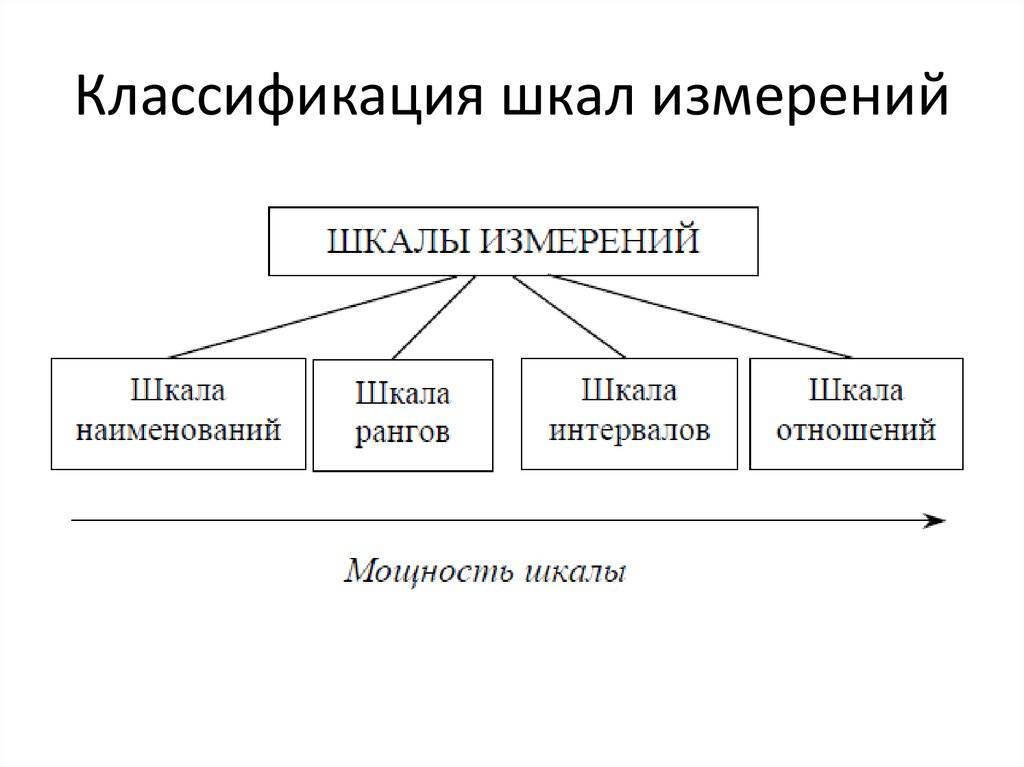
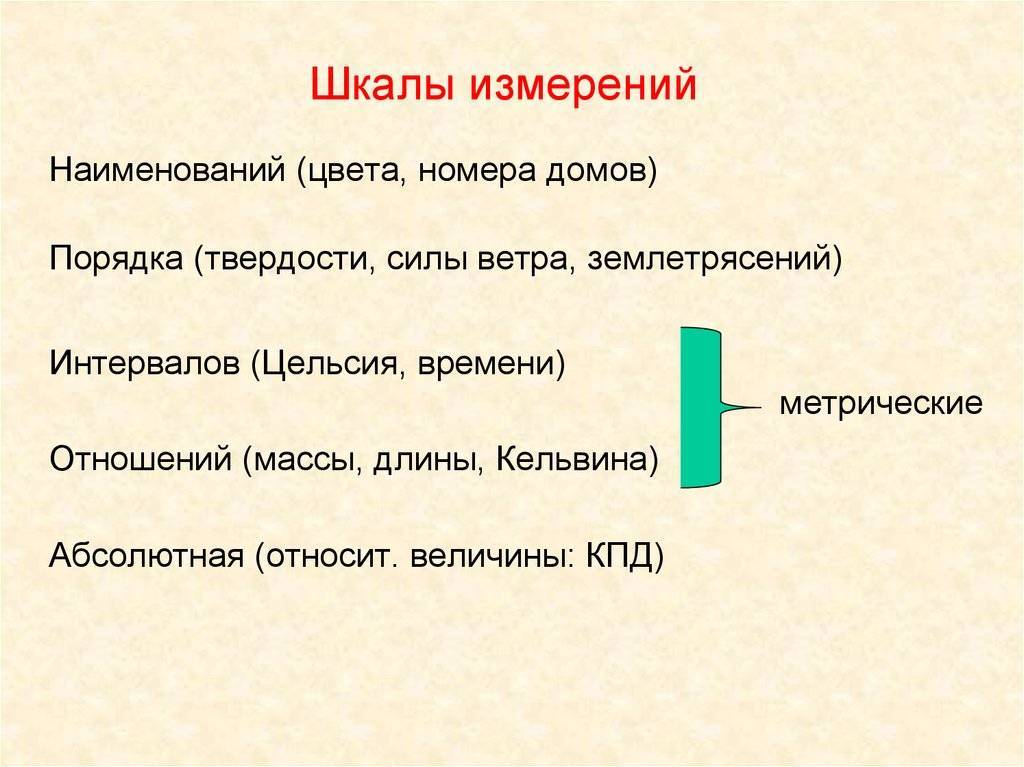
Первая классификация шкал была предложена С. Стивенсом в 1946 г. и от современной общепринятой классификации принципиально не отличается.Шкалы, как правило, объединяют в три основные группы:

• номинальные — для качественных измерений;
• порядковые — для отражения отношения порядка (больше, лучше, важнее, проще, правильнее и т. п.);
• количественные — оперируют с числами так, как мы привыкли со школьных времен (например, 10 в 2 раза больше, чем 5).

Иногда все шкалы измерения делят на два класса:

• шкалы качественных признаков (порядковая шкала и шкала наименований);
• шкалы количественных признаков (количественные шкалы).

Далее мы последовательно разберём все типы шкал.

Как считать очки в десятиборье?

Сегодня в мужском легкоатлетическом десятиборье за удачное выступление в каждом виде спорта участнику начисляется около 1000 очков. Но какой результат, по вашему мнению, берётся за 1000? Первое, что приходит на ум, — взять за 1000 очков мировой рекорд для женщин. Но какой именно? Текущий не годится, так как он меняется, а хотелось бы иметь возможность сравнений во времени и измерять рекорды. Но допустим, мы зафиксируем раз и навсегда, за что дается 1000 очков: в прыжках в длину, например, за 7,90 м, в беге на 100 метров — за 11 секунд. Далее возникает другой вопрос: какой шаг указать? Результат 8,00 м в прыжках в длину — это 1050 или 1010 очков? И как справедливо сравнивать разные виды соревнований? Думается, у каждого специалиста будут на этот счёт своё мнение и своя шкала.

Использование в психометрии

Основная статья: Психометрия

Используя различные шкалы, можно производить различные психологические измерения. Самые первые методы психологических измерений были разработаны в психофизике. Основной задачей психофизиков являлось то, каким образом определить, как соотносятся физические параметры стимуляции и соответствующие им субъективные оценки ощущений. Зная эту связь, можно понять, какое ощущение соответствует тому или иному признаку. Психофизическая функция устанавливает связь между числовым значением шкалы физического измерения стимула и числовым значением психологической или субъективной реакцией на этот стимул.

1.4. Основные технические характеристики

Манометрический прибор (манометр, вакуумметр, мановакуумметр, напоромер, тягомер, тягонапоромер, дифманометр и др.) – это средство измерения, которое определяется как техническое средство, предназначенное для измерений, имеющее нормированные метрологические характеристики, воспроизводящее и (или) хранящее единицу физической величины, размер которой принимают неизменным (в пределах установленной погрешности) в течение известного интервала времени/1-16/.

РМГ 29-99/1-16/, введенный взамен ГОСТ 16263-70, который устанавливал основные термины и определения в метрологии, определяет нижеследующее.

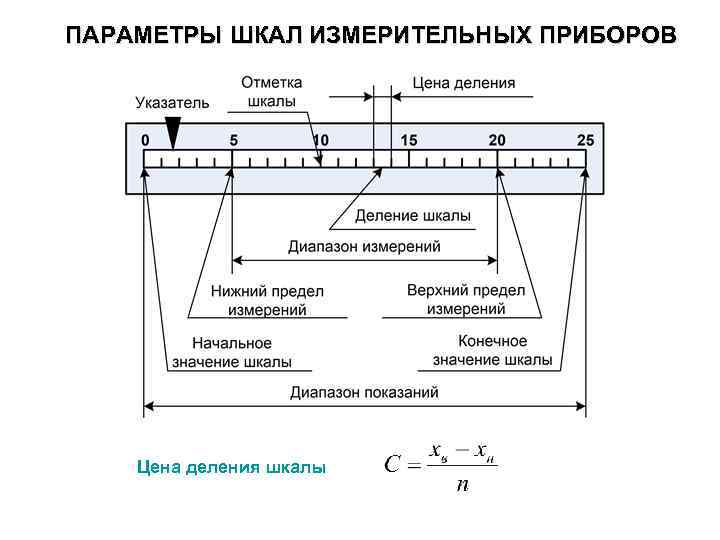
Шкала средства измерений – это часть показывающего устройства средства измерений, представляющая собой упорядоченный ряд отметок вместе со связанной с ними нумерацией.

Начальное значение шкалы – это наименьшее значение измеряемой величины, которое может быть отсчитано по шкале средства измерений.

Конечное значение шкалы – это наибольшее значение измеряемой величины, которое может быть отсчитано по шкале средства измерений.

Цена деления шкалы – это разность значения величины, соответствующих двум соседним отметкам шкалы средства измерений.

Диапазон показаний средства измерений – это область значений шкалы прибора, ограниченная начальным и конечным значениями шкалы

Отсчет показаний средства измерений — это фиксация значения величины или числа по показывающему устройству средства измерений в заданный момент времени. Погрешность результата измерения (погрешность измерения) — это отклонение результата измерения от истинного (действительного) значения измеряемой величины.

Систематическая погрешность измерения — это составляющая погрешности результата измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же физической величины. Случайная погрешность измерения — это составляющая погрешности результата измерения, изменяющаяся случайным образом (по знаку и значению) при повторных измерениях, проведенных с одинаковой тщательностью, одной и той же физической величины.

Точность результата измерений (точность измерений) – это одна из характеристик качества измерения, отражающая близость к нулю погрешности результата измерения. Неопределенность измерений — это параметр, связанный с результатом измерений и характеризующий рассеяние значений, которые можно приписать измеряемой величине. Погрешность средства измерений — это разность между показанием средства измерений и истинным (действительным) значением измеряемой физической величины. Приведенная погрешность средства измерений – это относительная погрешность, выраженная отношением абсолютной погрешности средства измерений к условно принятому значению величины, постоянному во всем диапазоне измерений или в части диапазона. Условно принятое значение величины называют нормирующим значением. Часто за нормирующее значение принимают верхний предел измерений. Приведенную погрешность обычно выражают в процентах

Стабильность средства измерений — это качественная характеристика средства измерений, отражающая неизменность во времени его метрологических характеристик. Основная погрешность средства измерений — это погрешность средства измерений, применяемого в нормальных условиях.

Дополнительная погрешность средства измерений — это составляющая погрешности средства измерений, возникающая дополнительно к основной погрешности вследствие отклонения какой-либо из влияющих величин от нормального ее значения или вследствие ее выхода за пределы нормальной области значений.

Класс точности средств измерений — это обобщенная характеристика данного типа средств измерений, как правило, отражающая уровень их точности, выражаемая пределами допускаемых основной и дополнительных погрешностей, а также другими характеристиками, влияющими на точность.

а) Диапазон показаний манометрических приборов должен выбираться из ряда, приведенного в табл. 1.2 (ГОСТ 2405–88/1-14/), и в технических условиях (ТУ) на прибор конкретного типа.

Этим ГОСТом допускается по заказу потребителя изготавливать приборы с диапазоном показаний, отличным от указанных в табл. 1.2.

Пределы измерения для

манометрических приборов согласно ГОСТ 2405-88/1-14/

Источник

Шкала наименований

Данная шкала еще называется номинальной. Она является самой простой. Числа в ней играют роль ярлыков. Они нужны для того, чтобы обнаруживать и различать изучаемые объекты. Числа, которые составляют данную шкалу, разрешено менять местами. В ней нет никаких отношений типа «меньше-больше». По этой причине некоторые думают, что ее применение не стоит принимать за измерение. Используя шкалу наименований, можно проводить лишь небольшое число математических операций. К примеру, нельзя вычитать и складывать ее числа, но можно посчитать, сколько раз встречается определенное число.

Меры длины

Величинами называют все, что поддается измерению. Так говорят о длине, площади, объеме, массе, времени, скорости. Величины — результат измерений, число, выраженное в определенных единицах. Последние известны как единица измерения.

Чтобы обозначить величину, пишут число, а рядом с ним указывают единицу, в которой проводилось измерение. К примеру, 3 см, 15 кг, 20 км, 2 мин. Для каждой величины общее число возможных значений не ограничено. Так, длина может быть 1 см, 10 см, 100 см и т. д. Одну и ту же величину в разных единицах выражают с помощью разных чисел.

Угловатый почерк: анализ, о чем он говорит

Кроме того, одну и ту же величину могут выражать по-разному. Например, используются различные единицы измерения длины в зависимости от того, насколько она маленькая или большая. В школе используются такие из них:

1. Наименьшая единица — миллиметр (мм). Его легко увидеть на самой обычной линейке, которая есть у каждого школьника. Это самое маленькое деление, а точнее расстояние между ними.
2. Следующей единицей стал сантиметр (см). На линейках сантиметры обозначаются числами. Один сантиметр состоит из десяти миллиметров. Между этими величинами ставится знак равенства, так как с их помощью обозначается одна и та же длина: 1 см = 10 мм.
3. За сантиметром следует дециметр (дм). Один дециметр состоит из десяти сантиметров. Эти величины также равны, что обозначается следующим уравнением: 1 дм = 10 см.
4. За дециметром следует метр (м), который содержит десять дециметров, то есть 1 м = 10 дм. В домашних условиях метр проще всего увидеть, если взять рулетку, длина которой часто составляет 1 метр. Сколько сантиметров в нем и как переводят сантиметры в метры? Один метр содержит десять дециметров, а они, в свою очередь, сто сантиметров (1 м = 10 дм = 100 см).
5. Самая большая единица в этой категории в рамках стандартной школьной программы — километр. Один километр состоит из тысячи метров, что обозначается так: 1 км = 1000 м. Километры используются для измерений расстояний между странами и городами. Можно, конечно, переводить миллиметры в метры и далее, но более крупные величины все же удобнее.

Китайский календарь беременности: 2021 год

Существуют и более крупные меры, например мегаметры, гигаметры, тераметры, но они выходят за рамки знаний, необходимых школьнику.

Таким образом, меры величин, с помощью которых можно измерить длину, таковы:

Уровень коэффициента

Шкала коэффициента в дополнение ко всем атрибутам, отражённым номинальным, порядковым и интервальным уровнями, отражает атрибут коэффициента. И снова вернёмся к результатам в таблице. Значения в колонке Z (показания секундомера Z) могут быть получены из показаний колонки U (секундомер U — истинное время) с помощью простой формулы:

Коэффициент измерений между Z и U остаётся одинаковым. Например, коэффициент соотношения (Sayyed/Shatakshi) в колонке Z (22/26) такой же, как и в колонке U (11/13). Глядя на колонку Z, можно уверенно заключить, что “Shweta бежал вдвое дольше, чем Surbhi”

Также обратите внимание, что точка отсчёта секундомера верна. Navjot не участвовал в забеге, поэтому в показаниях секундомеров U и Z мы видим 0

Отсюда следует, что шкала коэффициента имеет ‘абсолютный ноль’ (точку, где измеряемых качеств не существует). Например, ‘ноль градусов’ на шкале Кельвина (находящейся на уровне коэффициента) означает полное отсутствие температуры.

Большая часть научных и инженерных измерений выполняется на шкалах коэффициента. В науке измерение обычно определяется как вычисление коэффициента между значением непрерывной величины и величиной единицы измерения того же рода. Некоторые примеры измерений по шкале коэффициента: концентрация химического вещества, плотность потока фотосинтетических фотонов, температура в Кельвинах, масса, длина, время, угол на плоскости, энергия, давление и электрический заряд.

Определить по какой шкале производится измерение: интервальной или коэффициента можно, задав два вопроса: имеет ли здесь смысл ноль? Допустимы ли операторы удвоения или деления пополам?

Также важно отметить, что некоторые научные измерения не попадают ни в один из этих уровней. Их примеры включают шкалу pH и значения logIC50

Оба этих измерения проводятся по логарифмической шкале. Как бы то ни было, когда эти значения выражаются на шкале концентрации (H+ion концентрация для значений pH или IC50), измерения попадают в уровень коэффициента.

Класс — точность — измерительный прибор

Класс точности измерительного прибора — обобщенная характеристика прибора, определяемая пределами допускаемых основной и дополнительных погрешностей, а также другими свойствами прибора, влияющими на точность, значения которых устанавливаются в стандартах на отдельные виды средств измерений. Класс точности характеризует свойства приборов в отношении точности, но не является непосредственным показателем точности измерений, выполняемых с помощью этих приборов. Например, класс точности вольтметров характеризует пределы допускаемой основной погрешности и допускаемых изменений показаний, вызываемых внешним магнитным полем и отклонениями от нормальных значений температуры, частоты переменного тока и некоторых других влияющих величин.  

Класс точности измерительного прибора — это число, которое соответствует наибольшей погрешности, допустимой нормами. Класс точности выражается в процентах от верхнего предела измерения прибора. Например, термометр класса 1 может иметь допустимую погрешность 1 % от верхнего предела шкалы.  

Класс точности измерительного прибора определяется наибольшей допустимой погрешностью в процентах величины, соответствующей предельному значению шкалы прибора.  

Класс точности измерительных приборов нормируется как обобщенная характеристика средств измерений, определяемая пределами допускаемых основной и дополнительных погрешностей, а также другими свойствами средств измерений, влияющих на их точность, значения которых устанавливаются стандартами на соответствующие виды измерительных приборов.  

Классом точности измерительного прибора называется его характеристика, которая определяет степень точности измерения, пределы основной погрешности. Для приборов теплотехнического контроля холодильных установок класс точности численно равен максимальной величине приведенной основной погрешности, выраженной в процентах.  

Что характеризует класс точности измерительных приборов.  

Приведенная допустимая погрешность определяет класс точности измерительного прибора.  

Значение какой величины определяет обозначение класса точности измерительного прибора.  

Предельные значения основной и дополнительной погрешностей определяют класс точности измерительного прибора, который задается двумя способами: по величине абсолютной погрешности и по величине наибольшей допустимой основной приведенной погрешности в виде абсолютного числа, совпадающего с пределом допустимой погрешности для конечного значения рабочей части шкалы.  

В физико-химических иследованиях первый путь равносилен увеличению класса точности измерительных приборов или переходу к более прецизионным методам измерений. Второй путь представляется более доступным, но он пригоден лишь применительно к измерению экстенсивных величин. Кроме того, для успешного использования этого приема нужно быть уверенным в том, что абсолютная погрешность измерений не коррелирует с массой исследуемого образца и, следовательно, с измеряемым экстенсивным свойством. Так, если абсолютная погрешность измерения энтальпии сгорания для калориметра данной конструкции есть величина приблизительно постоянная для заданного интервала значений 100 — 5000 Дж, с целью снижения относительной погрешности определения следует сжигать навески, обеспечивающие большое тепловыделение.  

Максимальная погрешность этих измерений известна и определяется классом точности примененных измерительных приборов.  

При различных экспериментальных работах очень важно правильно выбрать класс точности используемых измерительных приборов. Под точностью прибора понимают его свойство, характеризующее степень приближения показаний данного прибора к действительным значениям измеряемой величины. Обычно точность прибора задается классом точности прибора или указывается в его паспорте

Очевидно, что чем точнее прибор, тем меньше его погрешность и выше стоимость.  

Обычно точность прибора задается классом точности прибора или указывается в его паспорте. Очевидно, что чем точнее прибор, тем меньше его погрешность и выше стоимость.  

Допустимое отношение сигнал / помеха зависит также от класса точности измерительного прибора.  

А ( / — ошибка измерения, которая определяется классом точности измерительного прибора; ДХ — допустимая погрешность измерения моделируемой величины.  

Особо специфическими являются требования, предъявляемые некоторыми стандартами в отношении класса точности измерительных приборов, применяемых при испытаниях.  

Для чего используются

Разнообразные виды измерительных трансформаторов встречаются как в небольших приборах размером со спичечный коробок, так и в крупных энергетических установках. Их основное назначение – понижать первичные токи и напряжения до значений, необходимых для измерительных устройств, защитных реле и автоматики. Применение понижающих катушек обеспечивает защиту цепи низшего и высшего ранга, поскольку они разделены между собой.

Понижающие средства разделяют по признакам эксплуатации и предназначены для:

• измерений. Они передают вторичный ток на приборы;
• защиты токовых цепей;
• применения в лабораториях. Такие понижающие средства имеют высокую классность точности;
• повторного конвертирования, они относятся к промежуточным инструментам.

Измерение

Измерительный трансформатор необходим для понижения высокого тока основного напряжения и передачу его на измерительные устройства. Для подключения стандартных приборов к высоковольтной сети потребовались бы громоздкие установки. Реализовывать инструменты таких размеров экономически не выгодно и не целесообразно.

Использование понижающих трансформаторов позволяет применять обычные устройства измерения в обычном режиме, что расширяет спектр их применения. Благодаря снижению напряжения, они не требуют дополнительных модификаций. Трансформатор отделяет высоковольтное напряжение сети от питающего напряжения приборов, обеспечивая безопасность из использования. От их классности зависит точность учета электрической энергии.

Защита

Кроме питания измерительных приборов понижающие трансформаторы подают напряжение на системы защиты и автоматической блокировки. Поскольку в сетевой электросети происходят перепады и скачки напряжения, которое губительно для высокоточного оборудования цепи.

В энергетических установках оборудование делится на силовое и вторичное, которое контролирует процессы первичной схемы подключения устройств. Высоковольтная аппаратура располагается на открытых площадках или устройствах. Вторичное оборудование находится на релейных планках внутри распределительных шкафов.

Промежуточным элементом передачи информации между силовыми агрегатами и средствами измерения, управления, контроля и защиты являются понижающие или измерительные трансформаторы. Они разделяют первичную и вторичную цепь от пагубного воздействия силовых агрегатов на чувствительные измерительные приборы, а также защищают обслуживающий персонал от повреждений.

Примечания

1. Журавлев Ю.И., Рязанов В. В., Сенько О. В. «Распознавание». Математические методы. Программная система. Практические применения. — М.: Фазис, 2006. ISBN 5-7036-0108-8.
2. ↑ Анфилатов В. С., Емельянов А. А., Кукушкин А. А. Системный анализ в управлении. — М. Финансы и статистика, 2002. — 368 с.
3. Перегудов Ф. И., Тарасевич Ф. П. Введение в системный анализ. — М.: Высшая школа, 1989. — 367 с.
4. ↑ Бахрушин В.Є. Методи аналізу даних. — Запоріжжя, КПУ, 2011
5. ↑
6. Mosteller, Frederick. Data analysis and regression : a second course in statistics (англ.). — Reading, Mass: Addison-Wesley Pub. Co, 1977. — ISBN 978-0201048544.
7. Wolman, Abel G. Measurement and meaningfulness in conservation science (англ.) // Conservation biology : journal. — 2006.
8. . Institute for Digital Research and Education. University of California, Los Angeles. Дата обращения: 7 февраля 2016.
9. Суппес П., Зиннес Д. Основы теории измерений // Психологические измерения. М.: 1967. С. 9-110.