О понятии жесткости. Жесткость пружины: формула
Определение
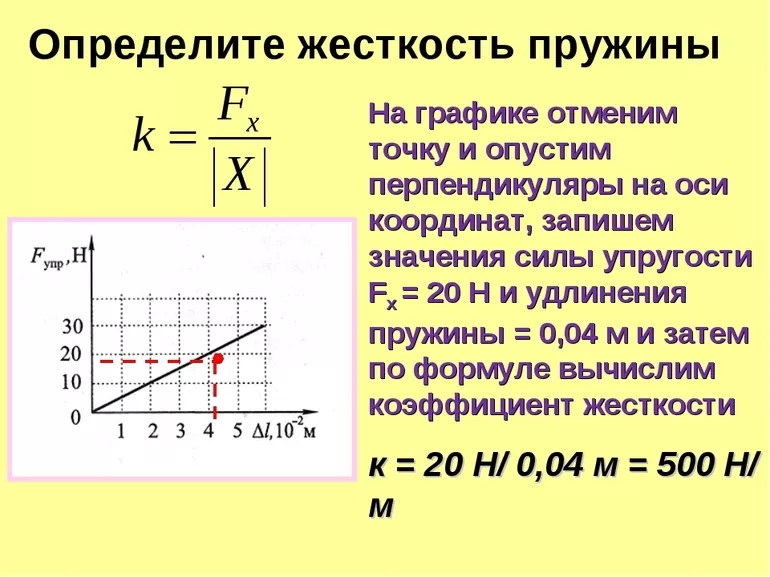
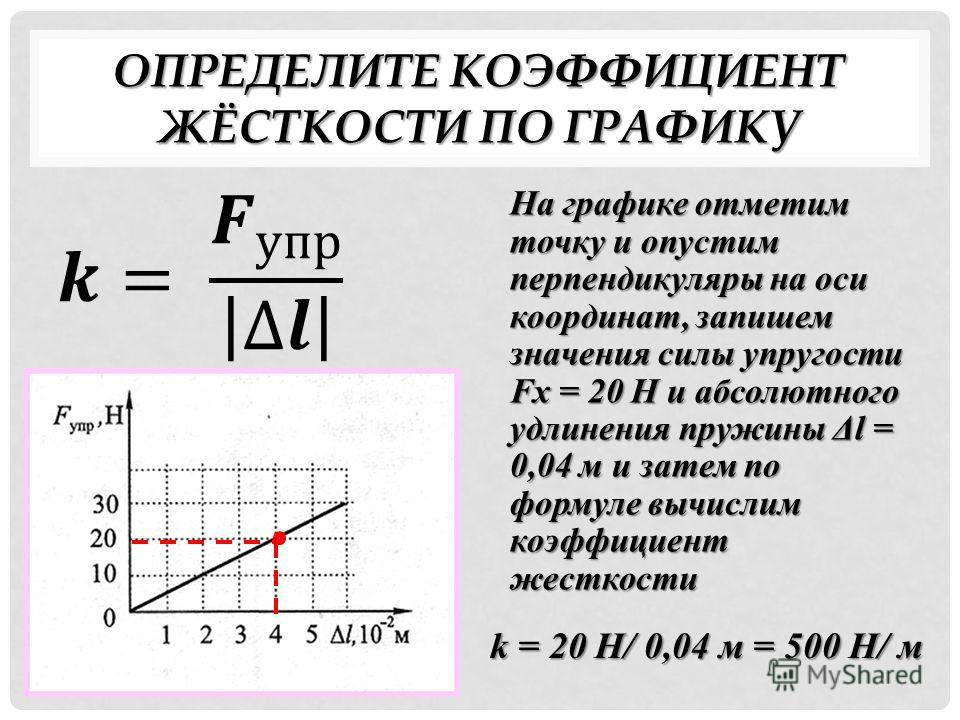
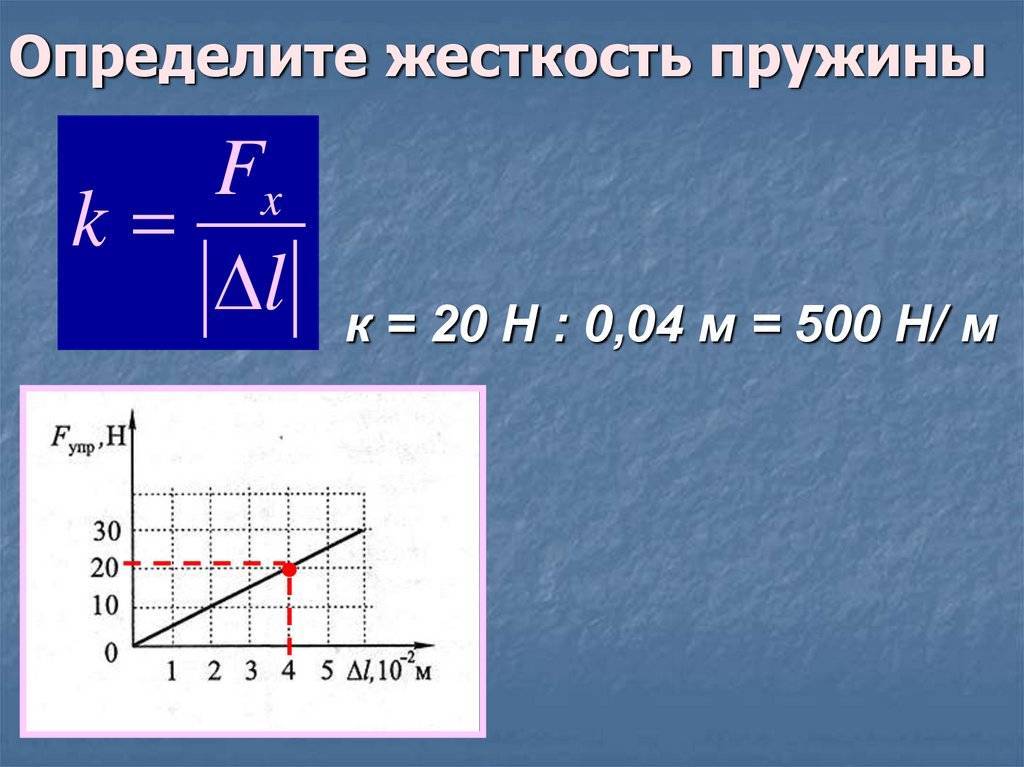
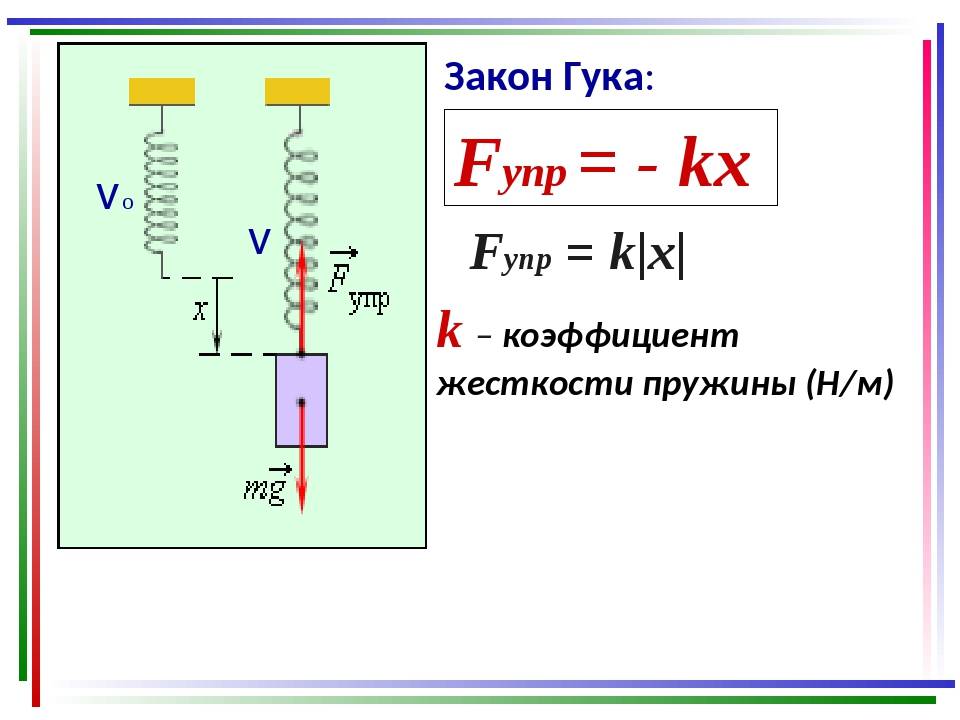
Жёсткостью пружины называют коэффициент, который связывает силу прилагаемую к ней с удлинением или сжатием.
Посмотрите на закон Гука.
Формула
Зако́н Гу́ка — утверждение, согласно которому, деформация, возникающая в упругом теле (пружине, стержне, консоли, балке и т. д.), пропорциональна приложенной к этому телу силе.
k – это и есть жёсткость пружины.
Fупр — сила жесткости или упругости пружины.
x — расстояние, на которое изменилась длина изделия после того как та была уравновешена.
Минус в формуле свидетельствует о том, что сила F имеет по сравнению с нагрузкой противоположное направление.
Закон Гука является одним из основных законов физики.
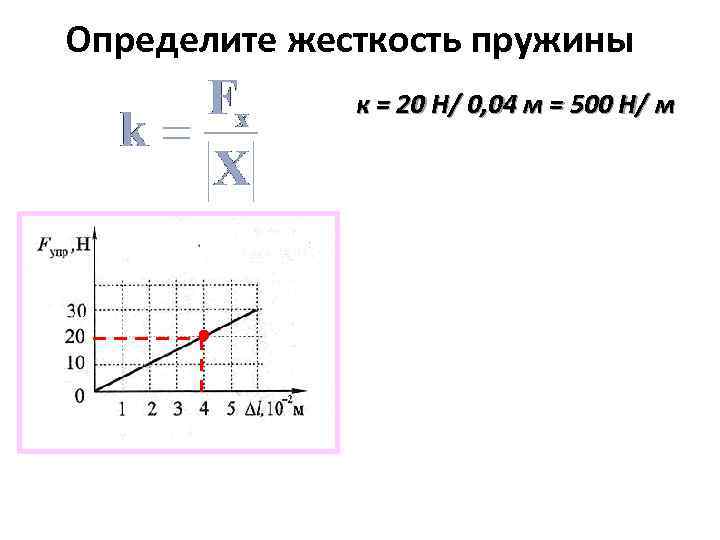
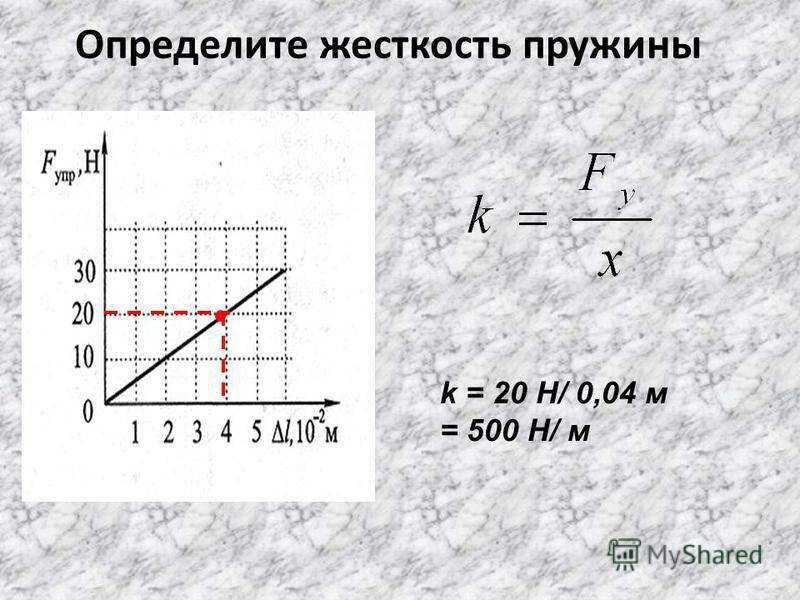
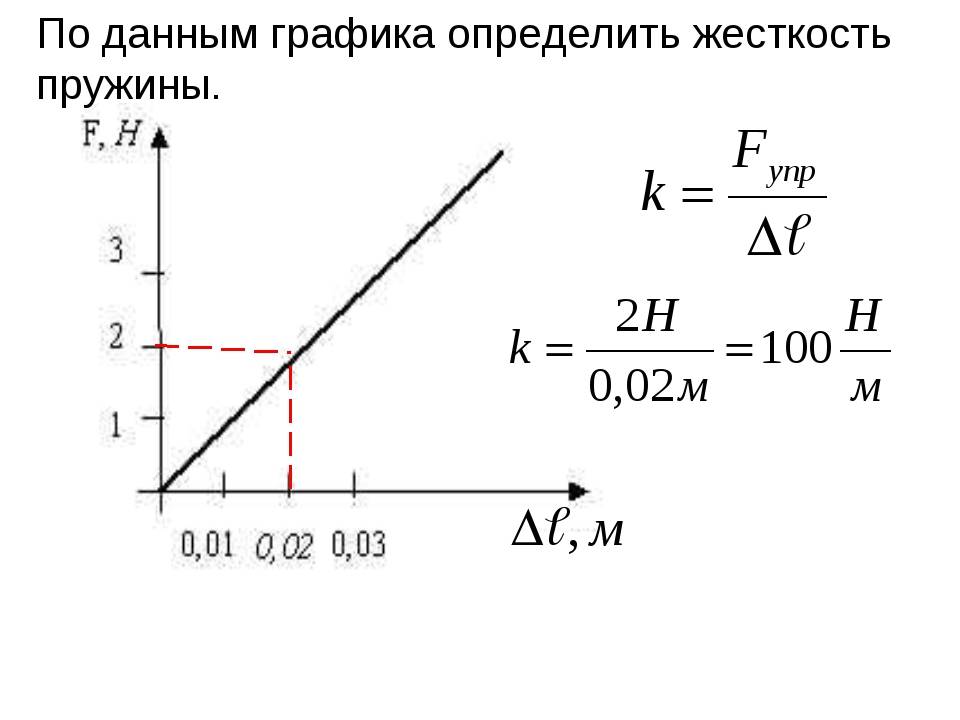
Как найти жесткость пружины? Формулу из выше приведённого уравнения понять достаточно легко:
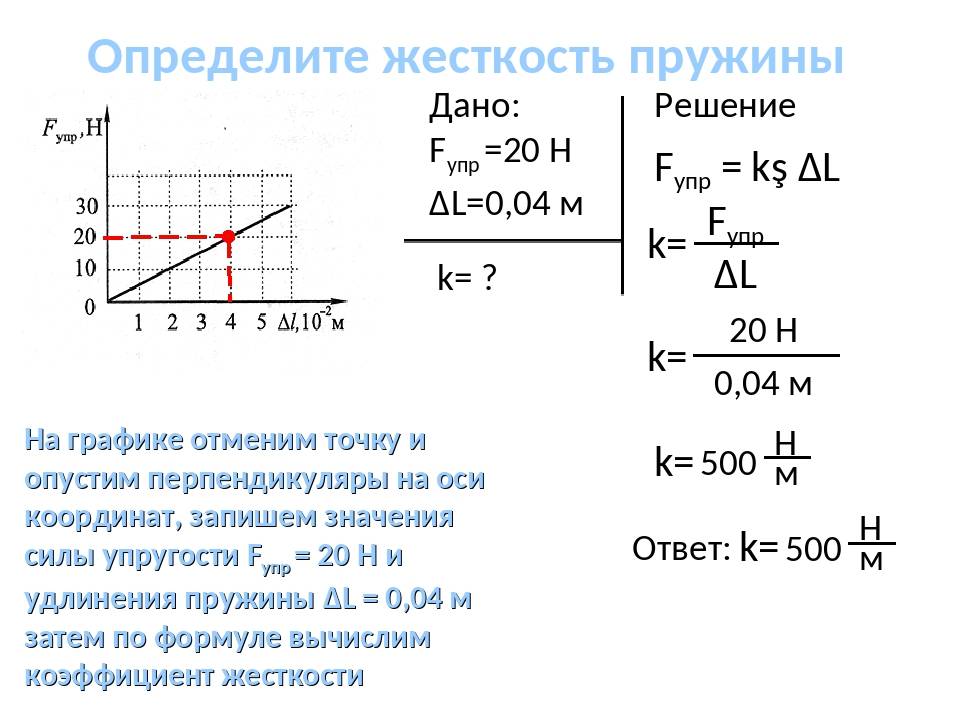
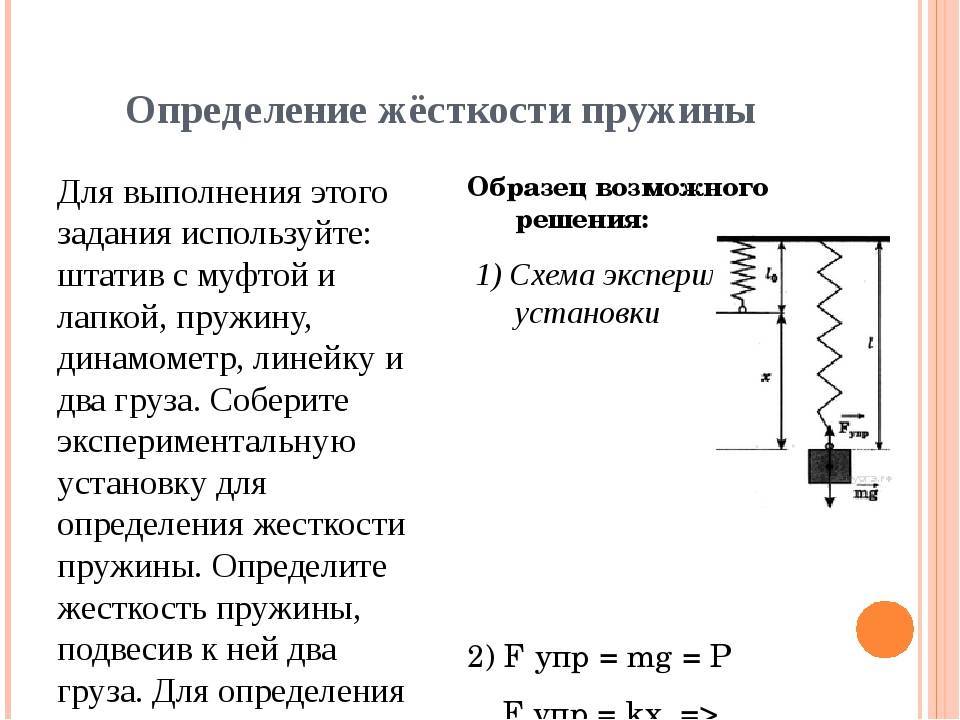
Коэффициент жесткости пружины можно вычислить и экспериментальным путём. Для этого нужно подвесить на вертикально закреплённую пружину груз с известной массой.
Имеем два уравнения:
Т. к. Fупр =Fтяж, получаем
Отсюда разделив обе части уравнения на x, найдём, что жёсткость равна
Массу самой пружины считаем равной нулю. Для исключения случайных ошибок проводим несколько измерений с грузами разной массы.
Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Нужна помощь
Как рассчитать жесткость цилиндрической пружины
В плоской пружине в момент её изгиба расстояния между молекулами, находящимися в одном месте уменьшаются, а в другом увеличиваются. Сила электромагнитных межмолекулярных связей стремится вернуть изделие в прежнее положение.
С цилиндрической пружиной всё несколько иначе. В ней энергия запасается не из-за деформации изгиба, а благодаря скручиванию проволоки вдоль своей оси навивания.
Давайте мысленно увеличим выполненное перпендикулярно её оси плоскостью сечение проволоки. Это нам позволит не учитывать спиральную форму изделия. Разобьём весь объём проволоки на очень много касающихся друг друга своими торцами цилиндров. Их диаметр совпадает с диаметром проволоки, а высота бесконечно мала. Торцам не дают разъединится действующие между ними межмолекулярные силы. Именно они препятствуют деформации.
Когда пружина растягивается или сжимается, цилиндры вынуждены вращаться друг относительно друга в противоположных направлениях вокруг общей оси. В каждом из сечений запасается некоторая энергия. Отсюда легко сделать вывод, что чем проволока длиннее, тем больше энергии такая пружина способна запасти. Увеличение проволоки по диаметру тоже способствует возрастанию её энергоёмкости.
Окончательная формула для жёсткости цилиндрической пружины такова:
Буквой R у нас обозначен радиус цилиндра пружины, n – количество витков проволоки, r—её радиус, G – коэффициент, индивидуальный для материала проволоки.
Чтобы по данной формуле сделать расчёт жёсткости, достаточно просто подставить вместо букв, обозначающих величины, их числовые значения.
Анна Краснова – Бакалавр физики
Умеешь писать статьи?Разбираешься в теме?
Начни писать статьи на заказ!
Популярные статьи
Изотермический процесс
Физика
Второй закон Ньютона
Физика
Взаимодействия гидроксидов алюминия и натрия
Химия
Виды правоотношений
Право и юриспруденция
Акты прокурорского реагирования
Право и юриспруденция
20 аминокислот с формулами
Биология
Квантовые постулаты Бора
Физика
Классификация растений
Биология
Основное свойство дроби
Математика
Виды монополий
Экономика
Общее понятие
При любом внешнем воздействии на предмет, внутри его возникают встречные силы, компенсирующие внешние. Для идеальных систем, находящихся в равновесии, силы равномерно распределены и равны, что позволяет сохранить форму предмета. Реальные системы не подчиняются таким правилам, что может привести к их деформации. Оценивая прочность материалов, говорят об их упругости.
Определение модуля Юнга твердых тел
Упругие материалы – это те, которые после прекращения внешнего воздействия, восстанавливают свою первоначальную форму.
Внутренние силы распределены равномерно по всей площади поперечного сечения предмета, имеют свою интенсивность, которая выражается количественно, называется напряжением (р) и измеряется в Н/м 2 или по международной системе Па.
Напряжение имеет свою пространственную направленность: перпендикулярно площади сечения предмета – нормальное напряжение (σz) и лежащая в плоскости сечения – касательное напряжение (τz).
Опыт с пружинными весами
Модуль упругости (Е) как единицу измерения отношения материала к линейной деформации, и нормальное напряжение связывает формула закона Гука:
где ε – относительное удлинение или деформация.
Преобразовав формулу (1) для выражения из нее нормального напряжения, можно увидеть, что Е является постоянной при относительном удлинении, и называется коэффициентом жесткости, а его единицы измерения Па, кгс/мм 2 или Н/м 2 :
Модуль упругости – это единица измерения отношения напряжения, создаваемого в материале, к линейной деформации, такой как, растяжение и сжатие.
В справочных материалах размерность модуля упругости выражается в МПа, так как деформация имеет довольно малое значение. А зависимость между этими величинами обратно пропорциональная. Таким образом, Е имеет высокое значение, определяемое 107-109.
Практические занятия
Механики и физики обозначают с помощью k, c и D коэффициент упругости, пропорциональности, жесткости. Смысл математической записи одинаковый. Численно показатель равняется силе, которая создаёт колебания на одну единицу длины. На практических работах по физике используется в качестве последней величины 1 метр.
Чем выше k, тем больше сопротивление предмета относительно деформации. Дополнительно коэффициент показывает степень устойчивости тела к колебаниям со стороны внешней нагрузки. Параметр зависит от длины и диаметра винтового изделия, количества витков, сырья. Единица измерения жесткости пружины — Н/м.
На практике перед школьниками и механиками может стоять более сложная задача, к примеру, найти общую жёсткость. В таком случае пружины соединены последовательным либо параллельным способом. В первом случае уменьшается суммарная жесткость. Если пружины расположены последовательно, используется следующая формула: 1/k = 1/k1 + 1/k2 + … + 1/ki, где:
- k — суммарная жёсткость соединений;
- k1 …ki — жёсткость каждого элемента системы;
- i — число пружин в цепи.
Если невесомые (расположены горизонтально) предметы соединены параллельно, значение общего k будет увеличиваться. Величина вычисляется по следующей формуле: k = k1 + k2 + … + ki.
Основная методика для вычислений
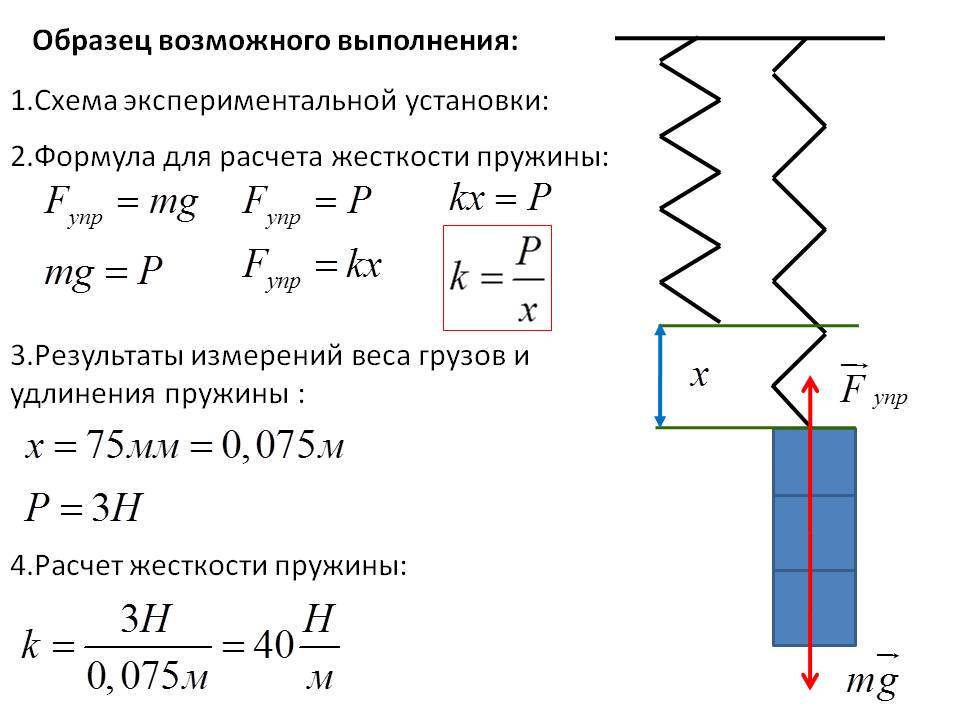
На практике коэффициент Гука определяется самостоятельно. Для эксперимента потребуется пружина, линейка, груз с определённой массой. Необходимо соблюдать следующую последовательность действий:
- Пружина фиксируется вертикально. Для этого используется любая удобная опора со свободной нижней частью.
- Линейкой измеряется длина предмета. Результат записывается как х1.
- На свободный конец подвешивается груз с известной массой m.
- Измеряется длина изделия под воздействием амплитуды. Вывод записывается как х2.
- Производит подсчёт абсолютного удлинения: x = x2-x1. Для определения энергии (силы) и k в международной системе СИ осуществляется перевод длины из разных единиц измерения в метры.
- Сила, спровоцировавшая деформацию, считается силой тяжести тела. Она рассчитывается по формуле: F = mg, где м является массой используемого груза (вес переводится в килограммы), а g (равен 9,8) — постоянная величина, с помощью которой отмечается ускорение свободного падения.
Если вышеописанные вычисления произведены, необходимо найти значение коэффициента жёсткости. Используется закон Гука, из которого следует, что k=F/x.
Решение задач
Для нахождения жёсткости в случае использования разных предметов, включая пружинные маятники с разной частотой колебаний, применяется формула Гука либо следствие, вытекающее из неё.
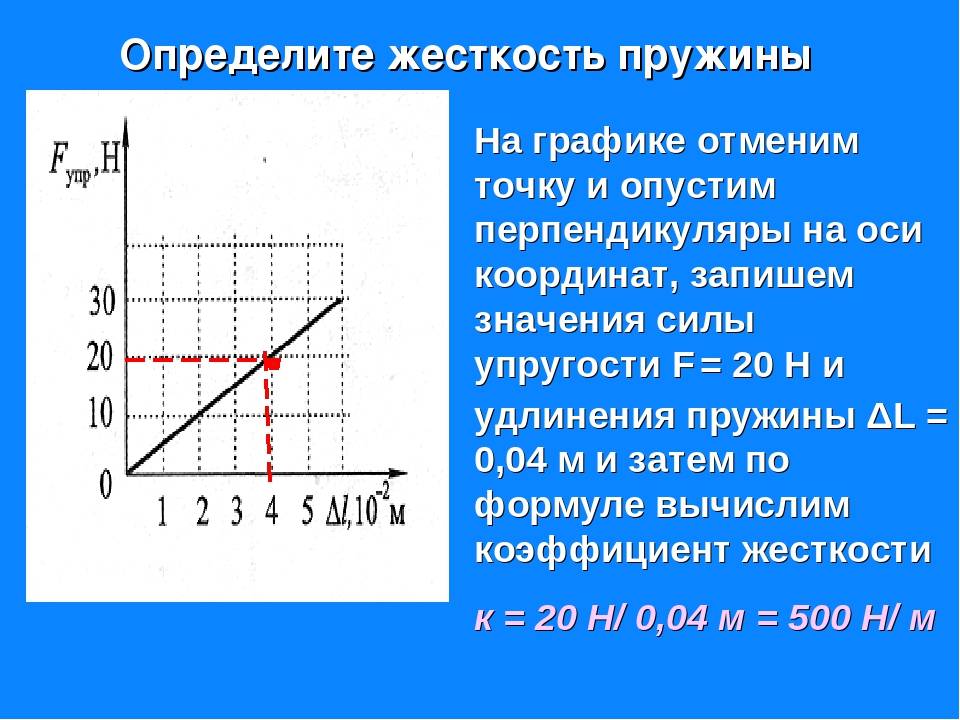
Задача № 1. Пружина имеет длину 10 см. На неё оказывается сила в 100 Н. Изделие растянулось на 14 см. Нужно найти k.
Решение: предварительно вычисляется абсолютное удлинение: 14−10=4 см. Результат переводится в метры: 0,04 м. Используя основную формулу, находится k. Его значение равняется 2500 Н/м.
Задача № 2. На пружину подвешивается груз массой 10 кг. Изделие растягивается на 4 см. Нужно найти длину, на которую растянется пружина, если использовать груз массой в 25 кг.
Решение: Определяется сила тяжести путем умножения 10 кг на 9.8. Результат записывается в Ньютонах. Определяется k=98/0.04=2450 Н/м. Рассчитывается, с какой силой воздействует второй груз: F=mg=245 Н. Для нахождения абсолютного удлинения используется формула x=F/k. Во втором случае х равняется 0,1 м.
Формула определения жесткости
Изучаемая современными школьниками формула, как найти коэффициент жесткости пружины, представляет собой соотношение силы и величины, показывающей изменение длины пружины в зависимости от величины данного воздействия (или
Читать также: Инструмент для установки резьбовых заклепок
равной ему по модулю силы упругости). Выглядит эта формула так: F = –kx. Из этой формулы коэффициент жесткости упругого элемента равен отношению силы упругости к изменению его длины. В международной системе единиц физических величин СИ он измеряется в ньютонах на метр (Н/м).
Другой вариант записи формулы: коэффициент Юнга
Деформация растяжения/сжатия в физике также может описываться несколько видоизмененным законом Гука. Формула включает значения относительной деформации (отношения изменения длины к ее начальному значению) и напряжения (отношения силы к площади поперечного сечения детали). Относительная деформация и напряжение по этой формуле пропорциональны, а коэффициент пропорциональности – величина, обратная модулю Юнга.
Модуль Юнга интересен тем, что определяется исключительно свойствами материала, и никак не зависит ни от формы детали, ни от ее размеров.
К примеру, модуль Юнга для ста
ли примерно равен единице с одиннадцатью нулями (единица измерения – Н/кв. м).
Смысл понятия коэффициент жесткости
Коэффициент жесткости – коэффициент пропорциональности из закона Гука. Еще он с полным правом называется коэффициентом упругости.
Фактически он показывает величину силы, которая должна быть приложена к упругому элементу, чтобы изменить его длину на единицу (в используемой системе измерений).
Значение этого параметра зависит от нескольких факторов, которыми характеризуется пружина:
- Материала, используемого при ее изготовлении.
- Формы и конструктивных особенностей.
- Геометрических размеров.
По этому показателю можно сд
елать вывод, насколько изделие устойчиво к воздействию нагрузок, то есть каким будет его сопротивление при приложении внешнего воздействия.
Особенности расчета пружин
Показывающая, как найти жесткость пружины, формула, наверное, одна из наиболее используемых современными конструкторами. Ведь применение эти упругие детали находят практически везде, то есть требуется просчитывать их поведение и выбирать те из них, которые будут идеально справляться с возложенными обязанностями.
Закон Гука весьма упрощенно показывает зависимость деформации упругой детали от прилагаемого усилия, инженерами используются более точные формулы расчета коэффициента жесткости, учитывающие все особенности происходящего процесса.
- Цилиндрическую витую пружину современная инженерия рассматривает как спираль из проволоки с круглым сечением, а ее деформация под воздействием существующих в системе сил представляется совокупностью элементарных сдвигов.
- При деформации изгиба в качестве деформации рассматривается прогиб стержня, расположенного концами на опорах.
Коэффициент жесткости пружины, формула и примеры
Определение и формула коэффициента жесткости пружины
Сила упругости (), которая возникает в результате деформации тела, в частности пружины, направленная в сторону противоположную перемещению частиц, деформируемого тела, пропорциональна удлинению пружины:
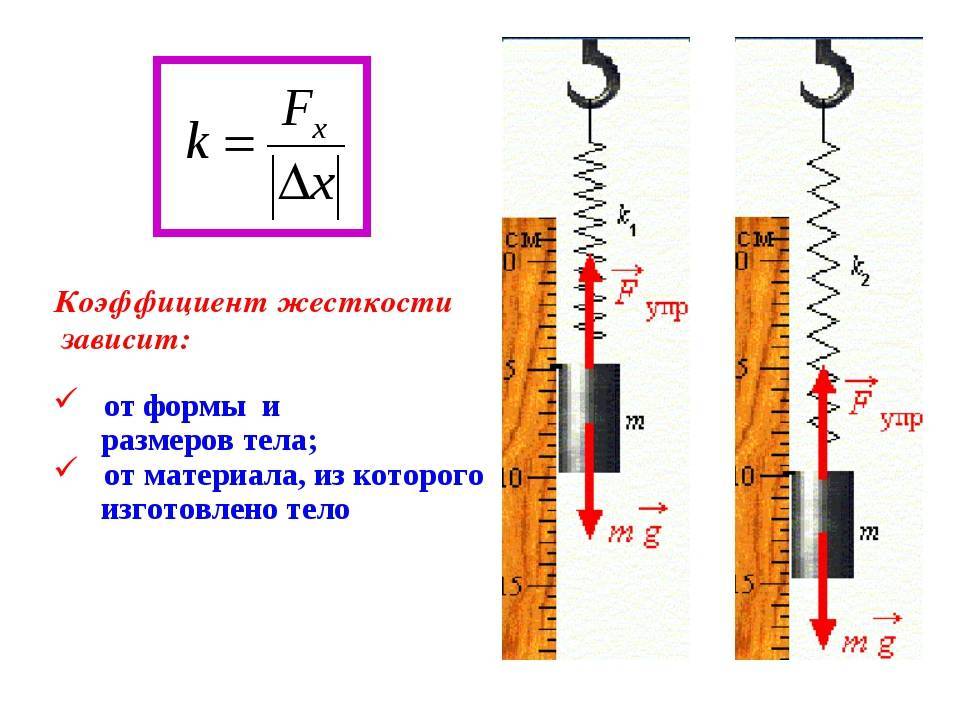
Он зависит от формы тела, его размеров, материала из которого изготовлено тело (пружина).
Иногда коэффициент жесткости обозначают буквами D и с.
Величина коэффициента жёсткости пружины указывает на устойчивость ее к действию нагрузок и насколько велико ее сопротивление при воздействии.
Коэффициент жесткости соединений пружин
Если некоторое число пружин соединить последовательно, то суммарную жесткость такой системы можно вычислить как:
В том случае, если мы имеем дело с n пружинами, которые соединены параллельно, то результирующую жесткость получают как:
Коэффициент жесткости цилиндрической пружины
Рассмотрим пружину в виде спирали, которая сделана из проволоки с сечением круг. Если рассматривать деформацию пружины как совокупность элементарных сдвигов в ее объеме под воздействие сил упругости, то коэффициент жесткости можно вычислить при помощи формулы:
где — радиус пружины, — количество витков в пружине, — радиус проволоки, — модуль сдвига (постоянная, которая зависит от материала).
Основной единицей измерения коэффициента жесткости в системе СИ является:
В СГС:
= дин/см
Коэффициент Пуассона — WiKi
Коэффициент Пуассона (обозначается как ν{\displaystyle \nu } или μ{\displaystyle \mu }) — величина отношения относительного поперечного сжатия к относительному продольному растяжению. Этот коэффициент зависит не от размеров тела, а от природы материала, из которого изготовлен образец. Коэффициент Пуассона и модуль Юнга полностью характеризуют упругие свойства изотропного материала. Безразмерен, но может быть указан в относительных единицах: мм/мм, м/м.
Приложим к однородному стержню растягивающие его силы. В результате воздействия таких сил стержень в общем случае окажется деформирован как в продольном, так и в поперечном направлениях.
Пусть l{\displaystyle l} и d{\displaystyle d} длина и поперечный размер образца до деформации, а l′{\displaystyle l^{\prime }} и d′{\displaystyle d^{\prime }} — длина и поперечный размер образца после деформации. Тогда продольным удлинением называют величину, равную (l′−l){\displaystyle (l^{\prime }-l)} , а поперечным сжатием — величину, равную −(d′−d){\displaystyle -(d^{\prime }-d)} . Если (l′−l){\displaystyle (l^{\prime }-l)} обозначить как Δl{\displaystyle \Delta l} , а (d′−d){\displaystyle (d^{\prime }-d)} как Δd{\displaystyle \Delta d} , то относительное продольное удлинение будет равно величине Δll{\displaystyle {\frac {\Delta l}{l}}} , а относительное поперечное сжатие — величине −Δdd{\displaystyle -{\frac {\Delta d}{d}}} . Тогда в принятых обозначениях коэффициент Пуассона μ{\displaystyle \mu } имеет вид:
Обычно при приложении к стержню растягивающих усилий он удлиняется в продольном направлении и сокращается в поперечных направлениях. Таким образом, в подобных случаях выполнятся Δll>0{\displaystyle {\frac {\Delta l}{l}}>0} и Δdd<0{\displaystyle {\frac {\Delta d}{d}}<0} , так что коэффициент Пуассона положителен. Как показывает опыт, при сжатии коэффициент Пуассона имеет то же значение, что и при растяжении.
Для абсолютно хрупких материалов коэффициент Пуассона равен 0, для абсолютно несжимаемых — 0,5. Для большинства сталей этот коэффициент лежит в районе 0,3, для резины он равен приблизительно 0,5.
Существуют также материалы (преимущественно полимеры), у которых коэффициент Пуассона отрицателен, такие материалы называют ауксетиками. Это значит, что при приложении растягивающего усилия поперечное сечение тела увеличивается.
К примеру, бумага из однослойных нанотрубок имеет положительный коэффициент Пуассона, а по мере увеличения доли многослойных нанотрубок наблюдается резкий переход к отрицательному значению −0,20.
Отрицательным коэффициентом Пуассона обладают многие анизотропные кристаллы, так как коэффициент Пуассона для таких материалов зависит от угла ориентации кристаллической структуры относительно оси растяжения. Отрицательный коэффициент обнаруживается у таких материалов, как литий (минимальное значение равно −0.54), натрий (−0.44), калий (−0.42), кальций (−0.27), медь (−0.13) и других. 67 % кубических кристаллов из таблицы Менделеева имеют отрицательный коэффициент Пуассона.
Уравнения колебаний пружинного маятника
Колебания пружинного маятника совершаются по гармоническому закону. Формула, по которой проводится расчет, выглядит следующим образом: F(t)=ma(t)=-mw2x(t).
В приведенной выше формуле указывается (w) радиальная частота гармонического колебания. Она свойственна силе, которая распространяется в границах применимости закона Гука. Уравнение движения может существенно отличаться, все зависит от конкретного случая.
Если рассматривать колебательное движение, то следует уделить внимание следующим моментам:
- Колебательные движения наблюдаются только в конце перемещения тела. Изначально оно прямолинейное до полного освобождения усилия. При этом сила упругости сохраняется на протяжении всего времени, пока тело находится в максимально отдаленном положении от нуля координат.
- После растяжения тело возвращается в исходное положение. Возникающая инерция становится причиной, по которой может оказываться воздействие на пружину. Инерция во многом зависит от массы тела, развитой скорости и многих других моментов.
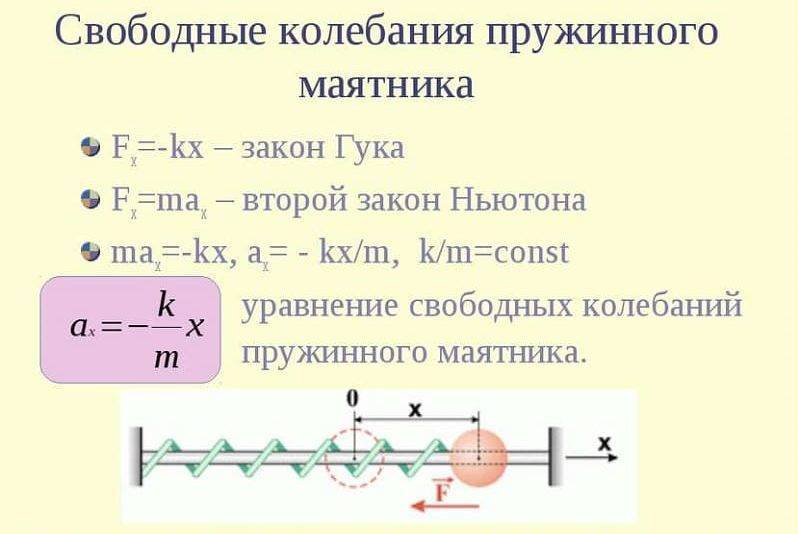
В результате этого возникает колебание, которое может длиться в течение длительного периода. Приведенная выше формула позволяет провести расчет с учетом всех моментов.
Деформация.
Силы упругости возникают при деформациях тел. Деформация — это изменение формы и размеров тела. К деформациям относятся растяжение, сжатие, кручение, сдвиг и изгиб.
Деформации бывают упругими и пластическими. Упругая деформация полностью исчезает после прекращения действия вызывающих её внешних сил, так что тело полностью восстанавливает форму и размеры. Пластическая деформация сохраняется (быть может, частично) после снятия внешней нагрузки, и тело уже не возвращается к прежним размерам и форме.
Частицы тела (молекулы или атомы) взаимодействуют друг с другом силами притяжения и отталкивания, имеющими электромагнитное происхождение (это силы, действующие между ядрами и электронами соседних атомов). Силы взаимодействия зависят о расстояний между частицами. Если деформации нет, то силы притяжения компенсируются силами отталкивания. При деформации изменяются расстояния между частицами, и баланс сил взаимодействия нарушается.
Например, при растяжении стержня расстояния между его частицами увеличиваются, и начинают преобладать силы притяжения. Наоборот, при сжатии стержня расстояния между частицами уменьшаются, и начинают преобладать силы отталкивания. В любом случае возникает сила, которая направлена в сторону, противоположную деформации, и стремится восстановить первоначальную конфигурацию тела.
Сила упругости — это сила, возникающая при упругой деформации тела и направленная в сторону, противоположную смещению частиц тела в процессе деформации. Сила упругости:
1. действует между соседними слоями деформированного тела и приложена к каждому слою;
2. действует со стороны деформированного тела на соприкасающееся с ним тело, вызывающее деформацию, и приложена в месте контакта данных тел перпендикулярно их поверхностям (типичный пример — сила реакции опоры).
Силы, возникающие при пластических деформациях, не относятся к силам упругости. Эти силы зависят не от величины деформации, а от скорости её возникновения. Изучение таких сил
выходит далеко за рамки школьной программы.
В школьной физике рассматриваются растяжения нитей и тросов, а также растяжения и сжатия пружин и стержней. Во всех этих случаях силы упругости направлены вдоль осей данных тел.
Особенности работы
Любая пружина представляет собой упругое изделие, которое в процессе эксплуатации подвергается статическим, динамическим и циклическим нагрузкам. Основная особенность этой детали – она деформируется под приложенным извне усилием, а когда воздействие прекращается – восстанавливает свою первоначальную форму и геометрические размеры. В период деформации происходит накопление энергии, при восстановлении – ее передача.
Именно это свойство возвращаться к исходному виду и принесло широкое распространение этим деталям: они отличные амортизаторы, элементы клапанов, предупреждающие превышение давления, комплектующие для измерительных приборов. В этих и других ситуациях, благодаря умению упруго деформироваться, они выполняют важную работу, поэтому от них требуется высокое качество и надежность.
Видео
Из этого видео вы узнаете, как определить жесткость пружины.
Суть метода заключается в том, что пружину нагружают силой определенной величины (в нашем случае, вес груза)
Дожидаются наступления статического равновесия пружины и замеряют ее деформацию под воздействием этой силы
Величина коэффициента жесткости
Далее определяются максимальное ( ) и минимальное ( ) значения коэффициента жесткости по следующим принципам
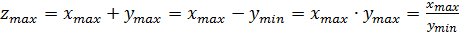, (12)
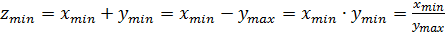, (13)
где , , , , , – максимальные и минимальные значения величин, задействованных в формулах.
Затем, поскольку коэффициент жесткости распределяется по симметричному «нормальному закону», по формулам, приведенным ниже для величин, определяются среднее значение коэффициента жесткости, половина доверительного интервала и относительная погрешность результата
(14)
(15)
. (16)
Определение коэффициента жесткости пружины методом строительной механики
Коэффициент жесткости определяется по зависимости
. (17)
С использованием формулы 17, а также зависимостей 12 и 13 определяются максимальное ( ) и минимальное ( ) значения коэффициента жесткости.
Затем, по формулам 14, 15 и 16 определяются среднее значение коэффициента жесткости, половина доверительного интервала и относительная погрешность результата.
ИТОГИ ЛАБОРАТОРНОЙ РАБОТЫ И ОФОРМЛЕНИЕ ОТЧЕТА
Итоги лабораторной работы
Анализируя полученные результаты необходимо сравнить методы определения коэффициента жесткости по критериям точности и сложности. Далее, дать оценку точности и достоверности полученных результатов, а также предложить меры по повышению точности результатов в случае неудовлетворительности последних.
Оформление отчета
Оформляется один отчет на бригаду на листах формата А4.
В отчете должны быть приведены все необходимые данные, расчеты и пояснения, результаты и выводы.
Отчет должен содержать следующие обязательные элементы: титульный лист с фамилиями выполнявших работу и проверяющего, оглавление с указанием номеров страниц начала разделов, нумерацию страниц, и разделы в следующем порядке:
1) исходные данные (см. п. 2.3),
2) определение статистических оценок измеренных величин,
3) определение коэффициента жесткости пружины статическим методом,
4) определение коэффициента жесткости пружины методом строительной механики,
Все появляющиеся первый раз переменные должны быть сопровождены пояснениями. Например,
деформация пружины – или
или
–модуль упругости стали при сдвиге.
У всех значений величин, имеющих размерность, должны стоять соответствующие единицы измерения. Все формулы должны быть раскрыты и сосчитаны. Например,
=176-138=38 мм.
Все рисунки и таблицы должны иметь названия и сквозную нумерацию.
СПИСОК ЛИТЕРАТУРЫ
1. Вентцель Е.С. Теория вероятностей. – М.: Наука, 1962. – 576 с.
2. ГОСТ 24026-80 Исследовательские испытания. Планирование эксперимента. Термины и определения.
3. Налимов В. В. Теория эксперимента – М.: Наука, 1971. – 207 с.
4. Румшиский Л.3. Математическая обработка результатов эксперимента – М.: Главная редакция физико-математической литературы изд-ва «Наука», 1971. – 192 с.
Приложение
| 0.9 | 0.95 | 0.98 | 0.99 | 0.999 | |
| 2.132 | 2.776 | 3.747 | 4.604 | 8.610 | |
| 2.015 | 2.571 | 3.365 | 4.032 | 6.859 | |
| 1.943 | 2.447 | 3.143 | 3.707 | 5.959 | |
| 1.895 | 2.365 | 2.998 | 3.499 | 5.405 | |
| 1.860 | 2.306 | 2.896 | 3.355 | 5.041 | |
| 1.833 | 2.262 | 2.821 | 3.250 | 4.781 | |
| 1.812 | 2.228 | 2.764 | 3.169 | 4.587 | |
| 1.796 | 2.201 | 2.718 | 3.106 | 4.487 | |
| 1.782 | 2.179 | 2.681 | 3.055 | 4.318 | |
| 1.771 | 2.160 | 2.650 | 3.012 | 4.221 | |
| 1.761 | 2.145 | 2.624 | 2.977 | 4.140 | |
| 1.753 | 2.131 | 2.602 | 2.947 | 4.073 | |
| 1.746 | 2.120 | 2.583 | 2.921 | 4.015 | |
| 1.734 | 2.103 | 2.552 | 2.878 | 3.922 | |
| 1.725 | 2.086 | 2.528 | 2.845 | 3.850 | |
| 1.708 | 2.060 | 2.485 | 2.787 | 3.725 | |
| 1.697 | 2.042 | 2.457 | 2.750 | 3.646 | |
| 1.689 | 2.030 | 2.437 | 2.724 | 3.591 | |
| 1.684 | 2.021 | 2.423 | 2.704 | 3.551 | |
| 1.679 | 2.014 | 2.412 | 2.689 | 3.522 | |
| 1.676 | 2.008 | 2.403 | 2.677 | 3.497 | |
| 1.671 | 2.000 | 2.390 | 2.660 | 3.460 | |
| 1.667 | 1.995 | 2.381 | 2.648 | 3.436 | |
| 1.664 | 1.990 | 2.374 | 3.639 | 3.416 | |
| 1.662 | 1.987 | 2.368 | 2.632 | 3.401 | |
| 1.660 | 1.984 | 2.364 | 2.626 | 3.391 | |
| 1.645 | 1.960 | 2.326 | 2.576 | 3.291 |
Учебно-методическое пособие по выполнению расчетных работ
Одерышев Андрей Васильевич
ОСНОВЫ НАУЧНЫХ ИССЛЕДОВАНИЙ
Печатается в авторской редакции
Подписано в печать Сдано в производство
Формат 1/16 Усл.-печ. л. Уч.-изд. л. 2.
Тираж 100 экз. Заказ №
Государственный университет морского и речного флота им. адм. С.О. Макарова,
198035, Санкт-Петербург, улица Двинская, 5/7
Отпечатали в типографии ФБОУ ВПО ГУМРФ
198035, Санкт – Петербург, Межевой канал, 2
Физические характеристики пружин
Цилиндрические пружины характеризуются рядом параметров, сочетание которых обуславливает их жесткость — способность сопротивляться деформации:
- материал; пружины чаще всего изготавливают из стальной проволоки, причем сталь в них применялася особая, ее характеризует среднее или высокое содержание углерода, низкое содержание других примесей (низколегированный сплав) и особая термообработка (закалка), придающая материалу дополнительную упругость;
- диаметр проволоки; чем он меньше, тем эластичнее пружина, но тем меньше ее способность запасать энергию; пружины сжатия изготавливают, как правило, из более толстой проволоки, чем пружины растяжения;
- форма сечения проволоки; не всегда проволока, из которой намотана пружина, имеет круглое сечение; уплощенное сечение имеют пружины сжатия, чтобы при максимальном сокращении длины (виток «садится» на соседний виток) конструкция была более устойчивой;
- длина и диаметр пружины; длину пружины следует отличать от длины проволоки, из которой она намотана; эти два параметра согласуются через количество витков и диаметр пружины, который, в свою очередь, не следует путать с диаметром проволоки.
Нужна консультация преподавателя в этой предметной области? Задай вопрос преподавателю и получи ответ через 15 минут! Задать вопрос
Существуют и другие физические характеристики, влияющие на работоспособность пружин. Например, при повышении температуры металл становится менее упругим, а при существенном ее понижении может стать хрупким. При интенсивной эксплуатации пружина со временем теряет часть упругости по причине постепенного разрушения связей между атомами кристаллической решетки.
Применение цилиндрических пружин
На производстве наиболее востребованы цилиндрические пружины, так как они обладают уникальными особенностями. При создании системы отмечается центральная ось, вдоль которой действуют разные силы. В процессе изготовления подобных изделий используется проволока соответствующего диаметра.
Для её изготовления понадобится специальный сплав либо обычные металлы. Сам материал должен обладать высокой упругостью. Проволока может иметь витки одного диаметра либо разных радиусов. Большим спросом пользуются цилиндрическая пружина, которая в сжатом состоянии обладает незначительной толщиной.
Главными параметрами изделия считаются:
- малый, средний и большой диаметр витков и самой проволоки;
- шаг размещения отдельный колец.
В задачах по физике вычисляется k для двух состояний: растяжение и сжатие. В любом случае используется одна формула для определения величины. Разница понятий:
- Исполнение, рассчитанное на сжатие, характеризуется дальним размещением витков. Расстояние, образуемое между ними, появляется возможность на сжатие.
- Модель, связанная с растяжением, имеет кольца, расположенные плотно между собой. Такая форма определяет то, что при максимальной силе растяжение минимальное.
Отдельно рассматриваются варианты на изгиб и кручение. Такие детали рассчитываются по специальным формулам. Для разных соединений характерны определённые особенности. Чтобы провести определения растяжения, учитывается момент теста.
Показатель зависит от характеристик проволоки, оказываемой силы либо массы тела. Для всех систем используются разные формулы, но полученные результаты не имеют погрешностей. Чтобы провести тесты для вычисления основных параметров, используется специальное оборудование. Простые задачи с деформацией пружин решают ученики на уроках физике в 7−8 классе. О параллельном и последовательном соединении элементов системы узнают учащиеся старших классов.
Как рассчитывают степень сжатия двигателя
Поскольку очень желательно, чтобы двигатель внутреннего сгорания, установленный на автомобиле, имел максимально возможную степень сжатия, то необходимо уметь ее определять
Важно это еще и для того, чтобы при регулировке силового агрегата, направленной на его форсирование, избежать опасности детонации, которая может просто разрушить мотор
Стандартная формула, по которой рассчитывается степень сжатия двигателя внутреннего сгорания, имеет следующий вид:
- CR=(V+C)/C,
- где CR — степень сжатия двигателя, V — рабочий объем цилиндра, C — объем камеры сгорания.
Для того чтобы определить значение этой величины для одного цилиндра, нужно сначала разделить общий рабочий объем силового агрегата на их количество. Таким образом определяется значение параметра V из приведенной выше формулы. Определить объем камеры сгорания (то есть значение величины С) несколько сложнее, но вполне возможно. Для этого опытные автомобилисты и механики, специализирующиеся на ремонте и наладке двигателей внутреннего сгорания, используют бюретку, которая проградуирована в кубических сантиметрах. Наиболее простой способ заключается в том, чтобы залить в камеру сгорания жидкость (например, бензин), а после этого измерить с помощью бюретки ее объем. Полученные данные нужно подставить в формулу расчета.
На практике значение степени сжатия двигателя обычно определяется в следующих случаях:
- При форсировании силового агрегата;
- При его приспособлении для функционирования с топливом другого октанового числа;
- После проведения такого ремонта ДВС, когда требуется корректировка степени сжатия.
Видео
Из этого видео вы узнаете, как определить жесткость пружины.
Суть метода заключается в том, что пружину нагружают силой определенной величины (в нашем случае, вес груза)
.
Дожидаются наступления статического равновесия пружины и замеряют ее деформацию под воздействием этой силы
.
Величина коэффициента жесткости
Далее определяются максимальное ( ) и минимальное ( ) значения коэффициента жесткости по следующим принципам
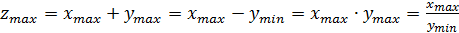, (12)
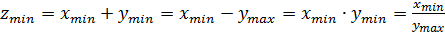, (13)
где , , , , , – максимальные и минимальные значения величин, задействованных в формулах.
Затем, поскольку коэффициент жесткости распределяется по симметричному «нормальному закону», по формулам, приведенным ниже для величин, определяются среднее значение коэффициента жесткости, половина доверительного интервала и относительная погрешность результата
(14)
(15)
. (16)
Определение коэффициента жесткости пружины методом строительной механики
Коэффициент жесткости определяется по зависимости
. (17)
С использованием формулы 17, а также зависимостей 12 и 13 определяются максимальное ( ) и минимальное ( ) значения коэффициента жесткости.
Затем, по формулам 14, 15 и 16 определяются среднее значение коэффициента жесткости, половина доверительного интервала и относительная погрешность результата.
ИТОГИ ЛАБОРАТОРНОЙ РАБОТЫ И ОФОРМЛЕНИЕ ОТЧЕТА
Итоги лабораторной работы
Анализируя полученные результаты необходимо сравнить методы определения коэффициента жесткости по критериям точности и сложности. Далее, дать оценку точности и достоверности полученных результатов, а также предложить меры по повышению точности результатов в случае неудовлетворительности последних.
Оформление отчета
Оформляется один отчет на бригаду на листах формата А4.
В отчете должны быть приведены все необходимые данные, расчеты и пояснения, результаты и выводы.
Отчет должен содержать следующие обязательные элементы: титульный лист с фамилиями выполнявших работу и проверяющего, оглавление с указанием номеров страниц начала разделов, нумерацию страниц, и разделы в следующем порядке:
1) исходные данные (см. п. 2.3),
2) определение статистических оценок измеренных величин,
3) определение коэффициента жесткости пружины статическим методом,
4) определение коэффициента жесткости пружины методом строительной механики,
Все появляющиеся первый раз переменные должны быть сопровождены пояснениями. Например,
деформация пружины – или
или
–модуль упругости стали при сдвиге.
У всех значений величин, имеющих размерность, должны стоять соответствующие единицы измерения. Все формулы должны быть раскрыты и сосчитаны. Например,
=176-138=38 мм.
Все рисунки и таблицы должны иметь названия и сквозную нумерацию.
СПИСОК ЛИТЕРАТУРЫ
1. Вентцель Е.С. Теория вероятностей. – М.: Наука, 1962. – 576 с.
2. ГОСТ 24026-80 Исследовательские испытания. Планирование эксперимента. Термины и определения.
3. Налимов В. В. Теория эксперимента – М.: Наука, 1971. – 207 с.
4. Румшиский Л.3. Математическая обработка результатов эксперимента – М.: Главная редакция физико-математической литературы изд-ва «Наука», 1971. – 192 с.
Приложение
| 0.9 | 0.95 | 0.98 | 0.99 | 0.999 | |
| 2.132 | 2.776 | 3.747 | 4.604 | 8.610 | |
| 2.015 | 2.571 | 3.365 | 4.032 | 6.859 | |
| 1.943 | 2.447 | 3.143 | 3.707 | 5.959 | |
| 1.895 | 2.365 | 2.998 | 3.499 | 5.405 | |
| 1.860 | 2.306 | 2.896 | 3.355 | 5.041 | |
| 1.833 | 2.262 | 2.821 | 3.250 | 4.781 | |
| 1.812 | 2.228 | 2.764 | 3.169 | 4.587 | |
| 1.796 | 2.201 | 2.718 | 3.106 | 4.487 | |
| 1.782 | 2.179 | 2.681 | 3.055 | 4.318 | |
| 1.771 | 2.160 | 2.650 | 3.012 | 4.221 | |
| 1.761 | 2.145 | 2.624 | 2.977 | 4.140 | |
| 1.753 | 2.131 | 2.602 | 2.947 | 4.073 | |
| 1.746 | 2.120 | 2.583 | 2.921 | 4.015 | |
| 1.734 | 2.103 | 2.552 | 2.878 | 3.922 | |
| 1.725 | 2.086 | 2.528 | 2.845 | 3.850 | |
| 1.708 | 2.060 | 2.485 | 2.787 | 3.725 | |
| 1.697 | 2.042 | 2.457 | 2.750 | 3.646 | |
| 1.689 | 2.030 | 2.437 | 2.724 | 3.591 | |
| 1.684 | 2.021 | 2.423 | 2.704 | 3.551 | |
| 1.679 | 2.014 | 2.412 | 2.689 | 3.522 | |
| 1.676 | 2.008 | 2.403 | 2.677 | 3.497 | |
| 1.671 | 2.000 | 2.390 | 2.660 | 3.460 | |
| 1.667 | 1.995 | 2.381 | 2.648 | 3.436 | |
| 1.664 | 1.990 | 2.374 | 3.639 | 3.416 | |
| 1.662 | 1.987 | 2.368 | 2.632 | 3.401 | |
| 1.660 | 1.984 | 2.364 | 2.626 | 3.391 | |
| 1.645 | 1.960 | 2.326 | 2.576 | 3.291 |
Учебно-методическое пособие по выполнению расчетных работ
Одерышев Андрей Васильевич
ОСНОВЫ НАУЧНЫХ ИССЛЕДОВАНИЙ
Печатается в авторской редакции
Подписано в печать Сдано в производство
Формат 1/16 Усл.-печ. л. Уч.-изд. л. 2.
Тираж 100 экз. Заказ №
Государственный университет морского и речного флота им. адм. С.О. Макарова,
198035, Санкт-Петербург, улица Двинская, 5/7
Отпечатали в типографии ФБОУ ВПО ГУМРФ
198035, Санкт – Петербург, Межевой канал, 2
