Длина общей нормали зубчатого колеса

Модуль шестерни

Шестерни используемые в Slot Car моделях

При конструировании Slot Car (трассовой модели), когда дело доходит до выбора шестерн, то перед нами открывается большой ассортимент на современном рынке с основной величиной модуля 0.3, 0.35 и 0.4. Основными характеристиками шестерни является количество зубьев, модуль шестерни, передаточное число. Если с количеством зубьев и передаточным числом (отношением количества зубьев ведомой к ведущей шестерни) все понятно, то с понятием модуль шестерни не совсем. К сожелению, в школах уже давно не тот уровень преподавания предмета черчения, а в большенстве случаях этот предмент не преподается.

И так, что такое модуль шестерни? Как вычисляется модуль шестерни и чем он обусловен? На этот вопрос нам помог учебник — Техническое черчение, изданный еще в 1972 году (как ни странно, на просторах современного интернета не так уж и много информации по данному вопросу).

Шестерни (на техническом языке — зубчатые колеса) служат для передачи движения от одного элемента машины к другому. Зубчатые колеса в зависимости от характера зацепления (внешнее или внутреннее), взаимного расположения вращающихся валов, способа передачи и т.д. могут быть самой различной конструкции. Наиболее распространенными являются цилиндрические и конические шестерни.

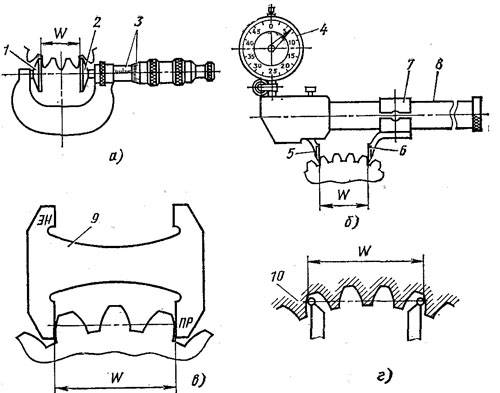
Рисунок 1 — Элементы зубчатого колеса (шестерни)

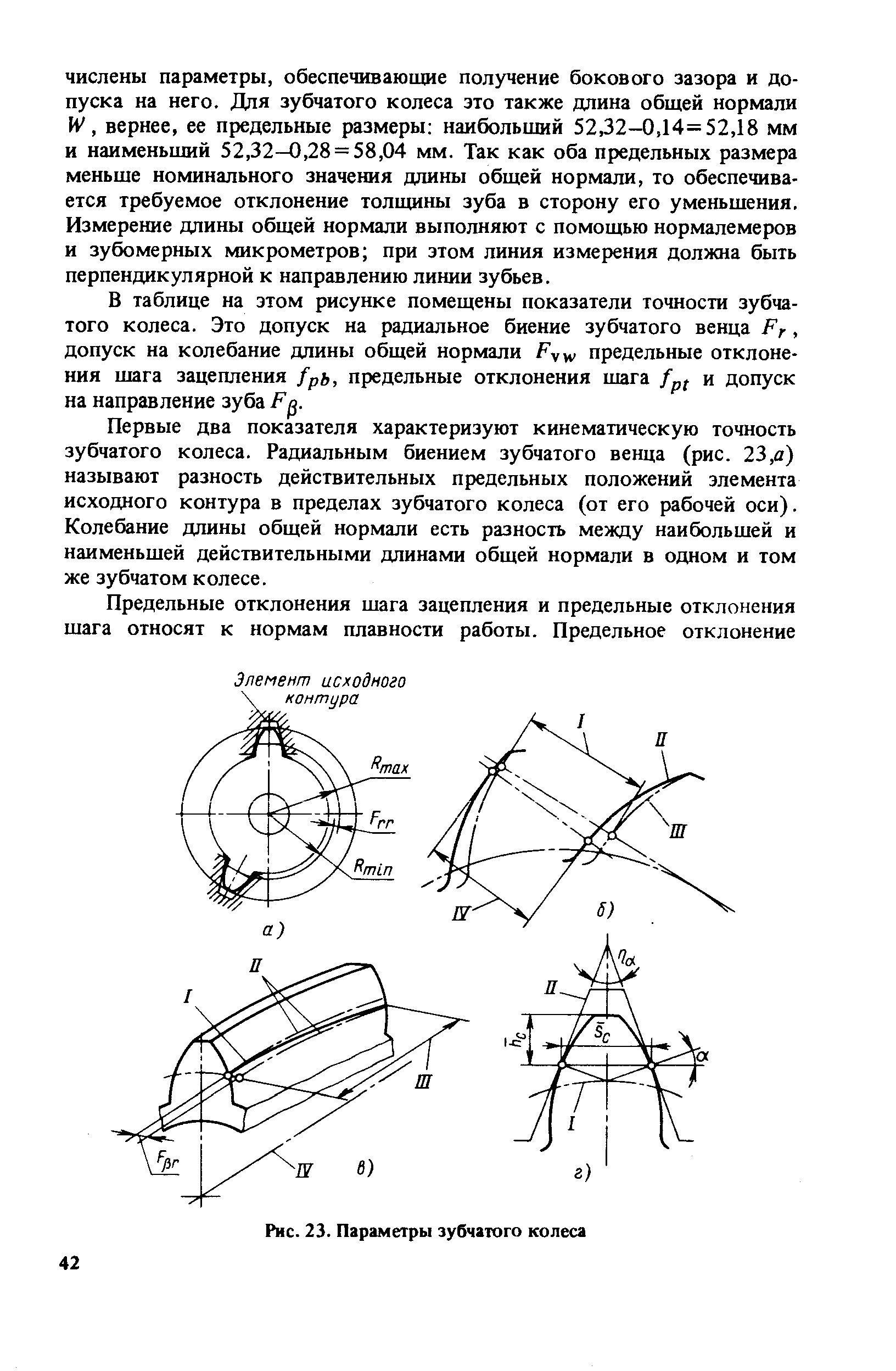
И так, из каких же элементов состоит шестерня (зубчатое колесо) изображенная на рисунке 1, а. Основным элементом шестерни является зуб (рисунок 1, б) — выступ определенной формы, предназначенный для передачи движения посредством воздействия на выступ другого элемента зубчатой передачи. Часть зубчатого колеса, в которую не входят зубья, называется телом зубчатого колеса (рисунок 1, в). Часть зубчатого колеса, состоящая из всех его зубьев и некоторой связывающей их части тела колеса, называется зубчатым венцом.

Впадиной называется пространство, заключенное между боковыми поверхностями соседних зубьев и поверхностями вершин и оснований впадин (рисунок 1, г).

Начальной поверхностью зубчатого колеса (рисунок 1, д) называется соосная поверхность, по которой катится без скольжения такая же поверхность друого колеа, находящегося в зацеплении с первым. Начальная поверхность колеса делит зуб на две части — головку и ножку.

На рисунке 1, е показано изображение на чертеже некоторых основных элементов зуба. Проекция поверхности выступв на плоскость, перпендикулярную оси зубчатого колеса, называется окружностью выступов, поверхность впадин — окружностью впадин, поверхность делительной поверхности — делительной окружностью. На этом чертеже обозначены высота зуба — h, головки зуба — h’ и ножки зуба — h’‘.

Торцовым шагом t3 называется расстояние по делительной окружности между одноименными профилями смежных зубьев. Диаметр делительной окружности — dд, диаметр окружности выступов — Dе, впадин — Di.

Модулем шестерни m называется отношение диаметра делительной окружности к числу зубьев Z:

Модуль шестерни (зубчатого колеса) можно выразить еще и как отношение торцового шага к числу π:

Высота головки зуба нормального зубчатого колеса примерно равна модулю h’=m, а высота ножки h»≈1,25 m. В соответствии с этими соотношениями можно установить следующую зависимость диаметра выступов De от модуля m и числа зубьев Z зубчатого колеса:

De = m (z + 2).

Рисунок 2 — Условное изображение конического зубчатого колеса (шестерни)

Для передачи движения между валами, оси которых пересекаются, применяются конические зубчатые колеса. Условное изображение конического зубчатого колеса показано на рисунке 2. В разрезе плоскостью, проходящей через ось колеса, зубья изображаются незаштрихованными. На виде, полученном проецированием на плоскость, перпендикулярную оси колеса, сплошными линиями изображаются окружности, соответствующие большому и малому выступу зубьев и штрих-пунктирной линией — окружность большого основания делительного конуса.

У конического зубчатого колеса имеются свои специфические элементы и соответствующие обозначения и размеры, отсутствующие у цилиндрического колеса:

Φ — угол делительного конуса;

Φе — угол конуса выступов;

Φi — угол конуса впадин;

L — конусное расстояние;

ν — угол внешнего дополнительного конуса.

Основные размеры некоррегированных конических зубчатых колес могут быть определены по следующим формулам.

Диаметр начальной окружности:

dд = m z.

Диаметр окружности выступов:

Dе = m (z + 2cos Φ).

Диаметр окружности впадин:

Di = m (z — 2,4cos Φ).

L= dд/(2cos Φ)

По материалам учебника «Техническое черчение» Авторы: Е.И Годик, В.М. Лысянский, В.Е. Михайленко, А.М. Пономарев. Киев. 1972г

Формула расчета параметров прямозубой передачи

Чтобы определить параметры прямозубой шестеренки, потребуется выполнить некоторые предварительные вычисления. Длина начальной окружности равна π×D, где D — ее диаметр.

Расчет модуля зубчатого колеса

Шаг зацепления t – это расстояние между смежными зубами, измеренное по начальной окружности. Если это расстояние умножить на число зубов z, то мы должны получить ее длину:

проведя преобразование, получим:

Если разделить шаг на число пи, мы получим коэффициент, постоянный для данной детали зубчатой передачи. Он и называется модулем зацепления m.

размерность модуля шестерни — миллиметры. Если подставить его в предыдущее выражение, то получится:

выполнив преобразование, находим:

Отсюда вытекает физический смысл модуля зацепления: он представляет собой длину дуги начальной окружности, соответствующей одному зубцу колеса. Диаметр окружности выступов D_e получается равным

где h’- высота головки.

Высоту головки приравнивают к m:

Проведя математические преобразования с подстановкой, получим:

Диаметр окружности впадин D_i соответствует D_e за вычетом двух высот основания зубца:

где h“- высота ножки зубца.

Для колес цилиндрического типа h“ приравнивают к значению в 1,25m:

Устройство зубчатого колеса

Выполнив подстановку в правой части равенства, имеем:

что соответствует формуле:

и если выполнить подстановку, то получим:

Иначе говоря, головка и ножка зубца относятся друг к другу по высоте как 1:1,25.

Следующий важный размер, толщину зубца s принимают приблизительно равной:

• для отлитых зубцов: 1,53m:
• для выполненных путем фрезерования-1,57m, или 0,5×t

Поскольку шаг t приравнивается к суммарной толщине зубца s и впадины s_в, получаем формулы для ширины впадины

• для отлитых зубцов: s_в=πm-1,53m=1,61m:
• для выполненных путем фрезерования- s_в= πm-1,57m = 1,57m

Характеристики конструкции оставшейся части зубчатой детали определяются следующими факторами:

• усилия, прикладываемые к детали при эксплуатации;
• конфигурация деталей, взаимодействующих с ней.

Детальные методики исчисления этих параметров приводятся в таких ВУЗовских курсах, как «Детали машин» и других. Модуль шестерни широко используется и в них как один из основных параметров.

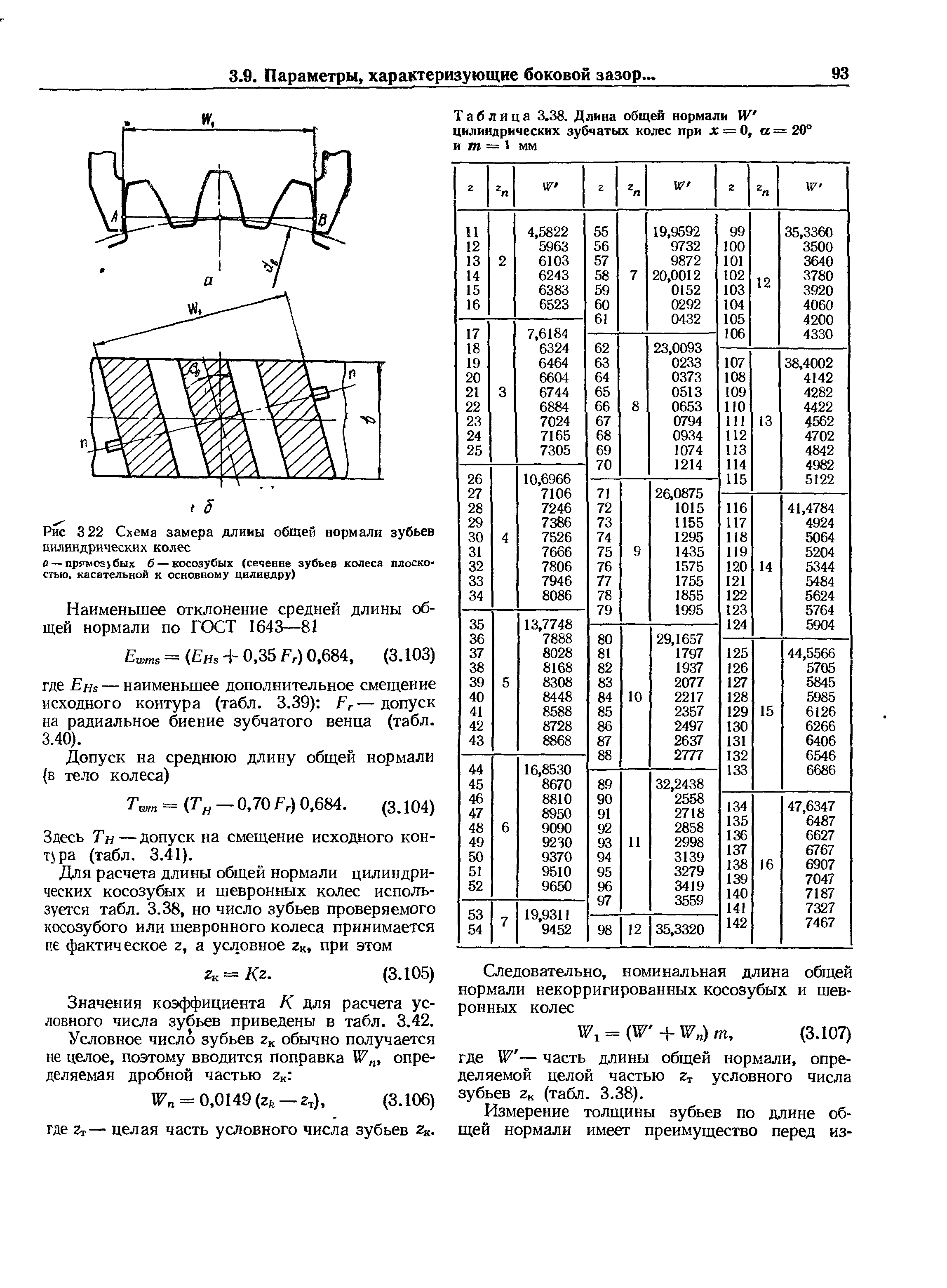
Для отображения шестеренок методами инженерной графики используются упрощенные формулы. В инженерных справочниках и государственных стандартов можно найти значения характеристик, рассчитанные для типовых размеров зубчатых колес.

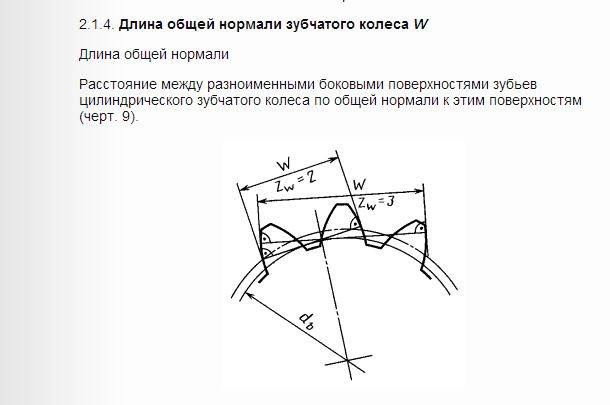
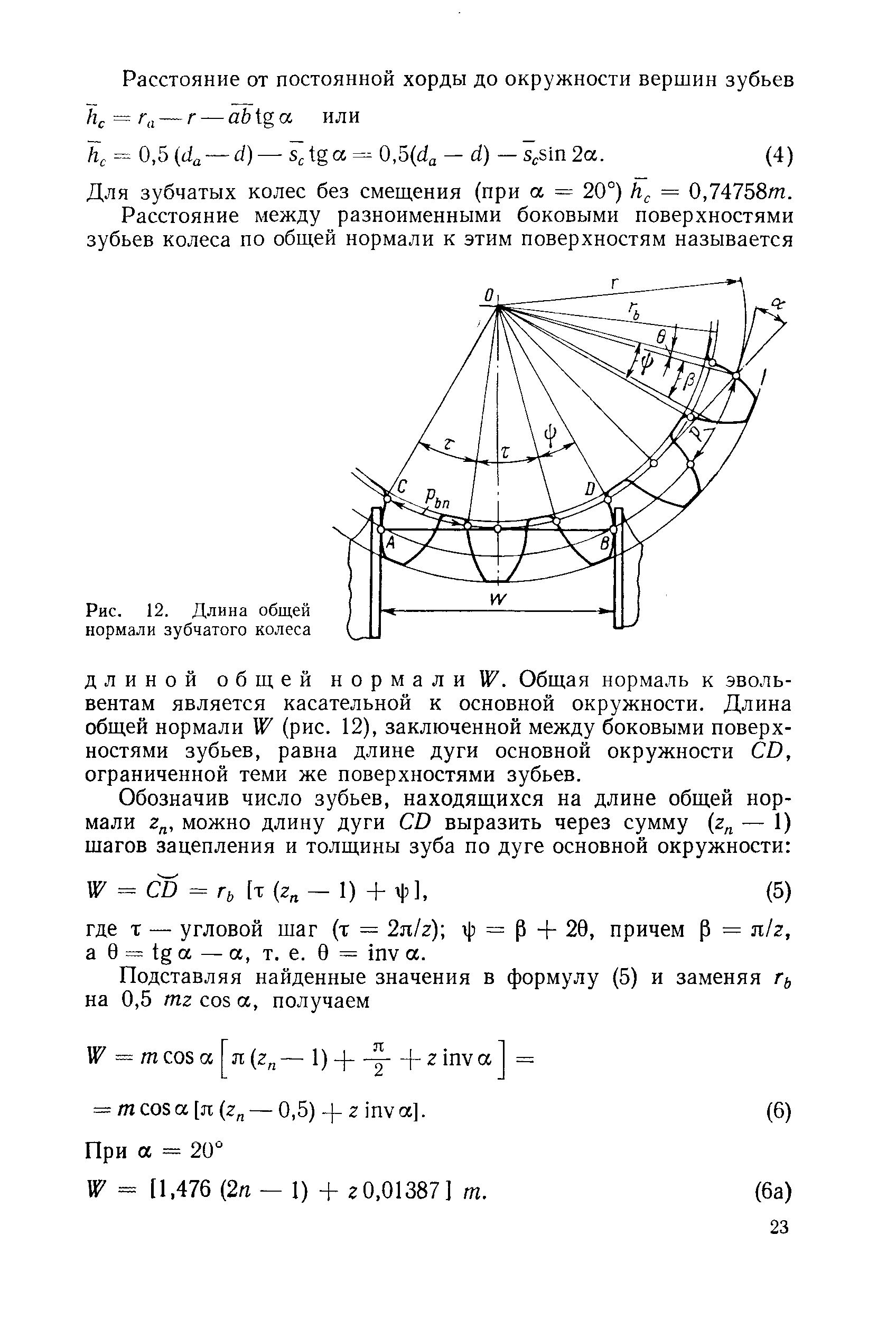
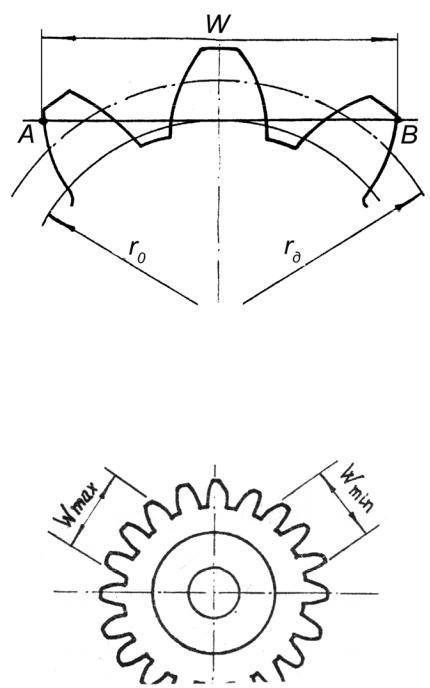
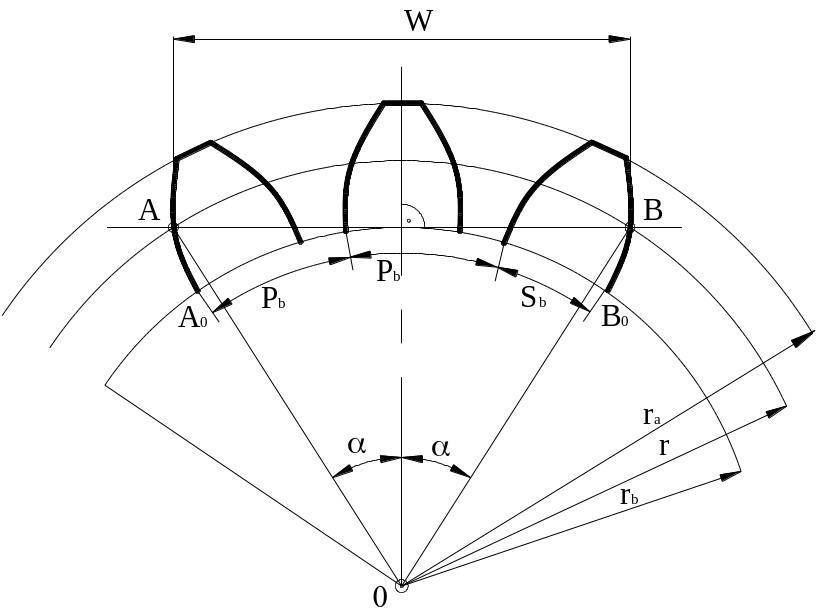
Что такое длина общей нормали?

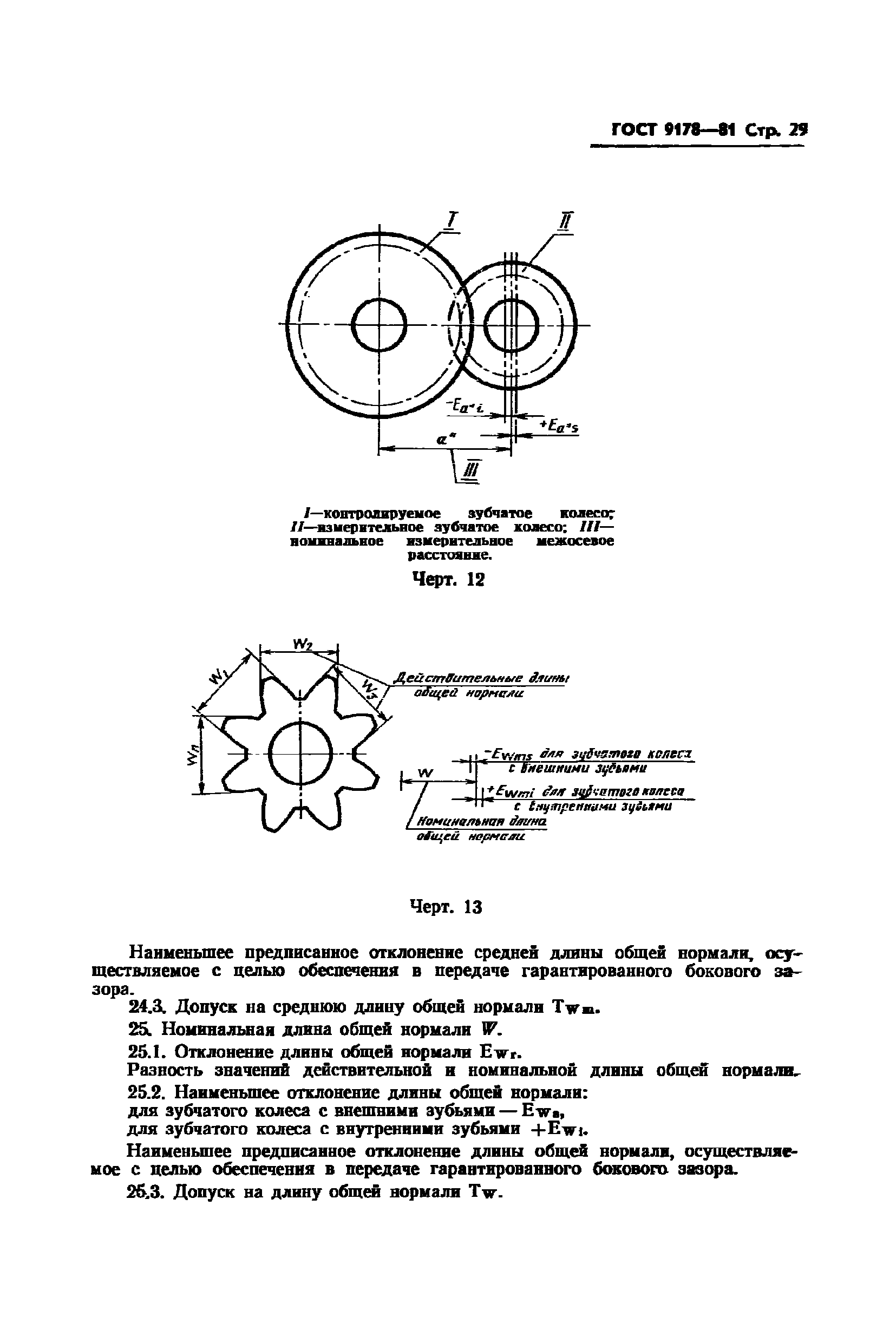
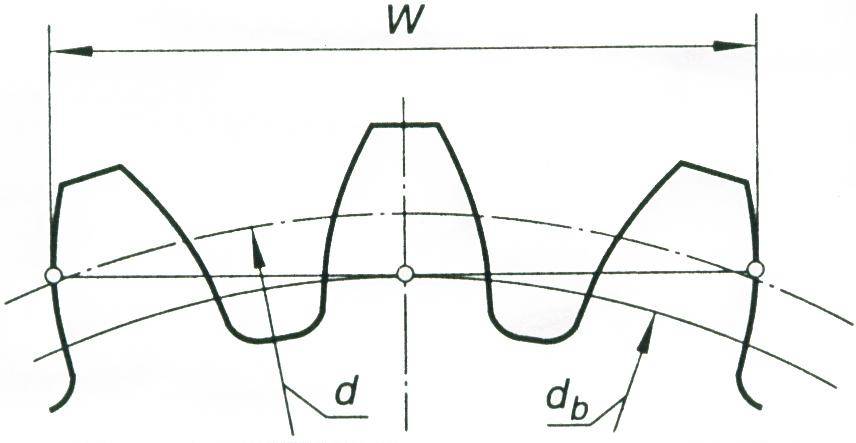
Для обеспечения функционирования механизма, представленного шестернями, проводится измерение основных показателей при использовании двух методов, один их которых предусматривает использование роликов, второй определение длины общей нормали

Рассматривая нормаль следует уделить внимание следующим моментам:

1. Практически все цилиндрические эвольвентные зубчатые передачи внешнего зацепления и другого типа производятся с учетом рассматриваемого показателя.
2. Длина определяется расстоянием между разноименными сторонам одной впадины.
3. Зависит подобный показатель от диаметров зубчатых колес, а также некоторых других параметров.

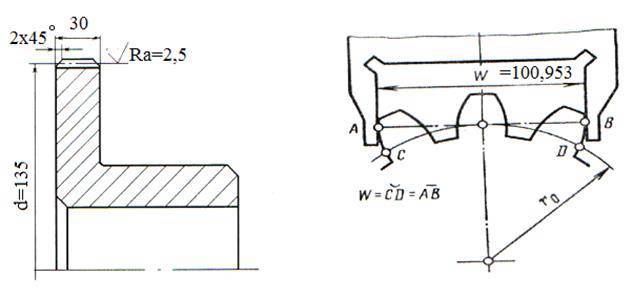
Определяется зачастую размер по роликам зубчатых колес. Подобный показатель указывается на чертежах, в большинстве случаев применяется для обозначения символ W.

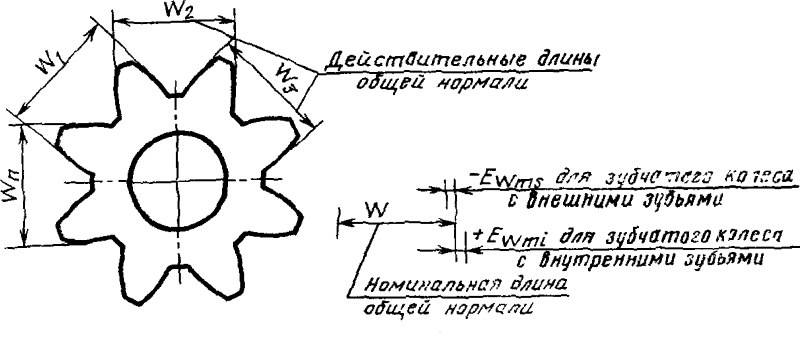
Еще довольно важным определением можно назвать то, что такое постоянная хорда. Она характеризуется отрезком прямой, которые соединяют две точки разноименных эвольвентных поверхностей зуба цилиндрического колеса. Этот показатель также часто отображается на чертеже, в большинстве случаев зуб изображается схематически.

ПРИЛОЖЕНИЕ 1 (рекомендуемое). УПРОЩЕННЫЙ РАСЧЕТ ГЕОМЕТРИЧЕСКИХ ПАРАМЕТРОВ

ПРИЛОЖЕНИЕ 1 Рекомендуемое

Таблица 1

Расчет некоторых основных геометрических параметров

Наименование параметра	Обозна- чение	Расчетные формулы и указания
Расчет коэффициента суммы смещений при заданном межосевом расстоянии
1. Коэффициент воспринимаемого смещения
2. Вспомогательная величина
	Определяется по номограмме на черт.1
	Определяется по графику на черт.2 Если =0, то =0
3. Коэффициент уравнительного смещения
4. Коэффициент суммы смещений
Расчет межосевого расстояния при заданных коэффициентах смещения и
5. Коэффициент суммы смещений
6. Вспомогательная величина
	Определяется по номограмме на черт.3

1.3. Допуски на измерительные размеры цилиндрических зубчатых колес

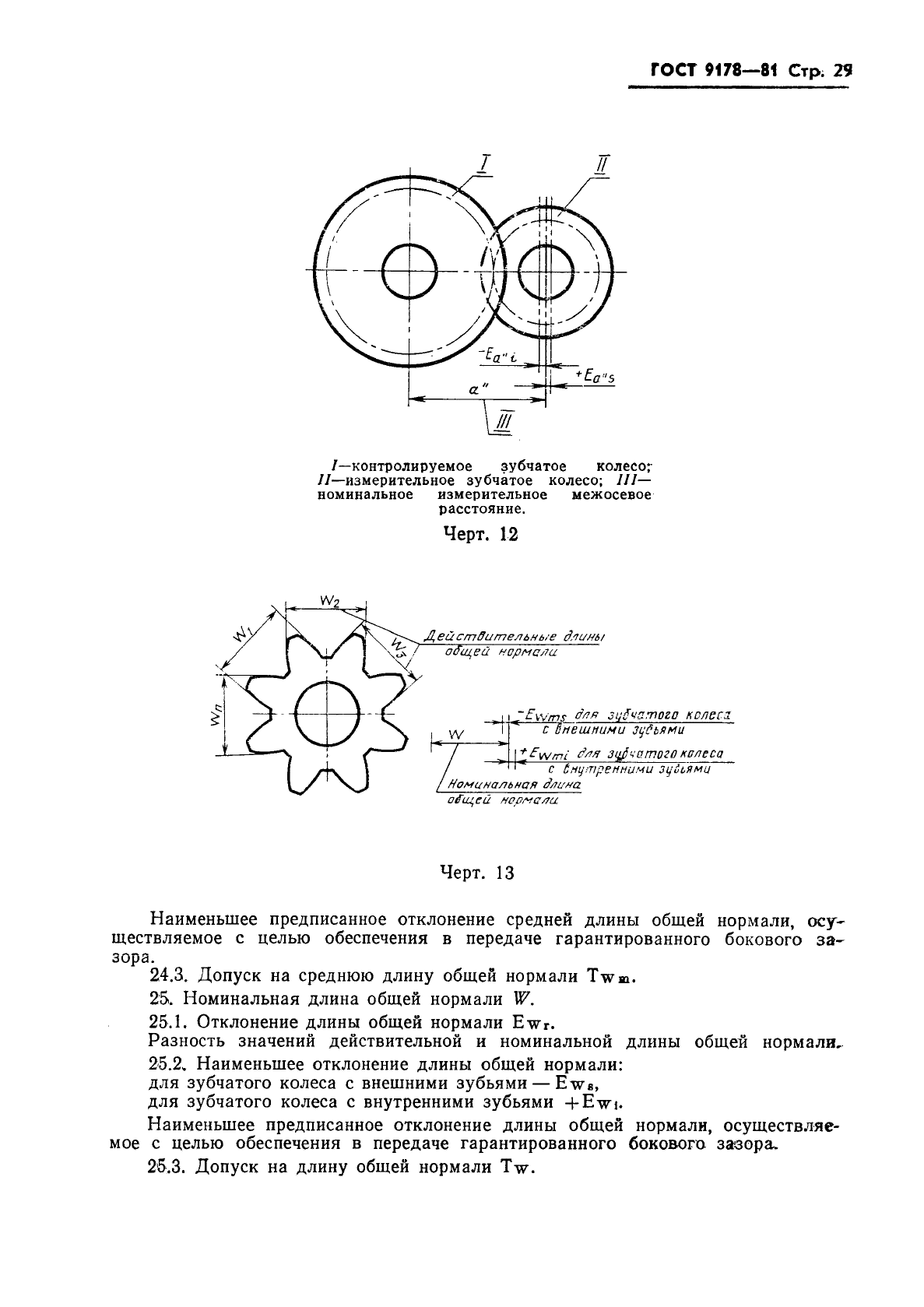
Рассмотренные выше формулы для вычисления номинальных измерительных размеров цилиндрических зубчатых колес гарантируют беззазорное зацепление колес в передаче. В реальных зубчатых передачах должен быть обеспечен гарантированный боковой зазор с целью устранения заклинивания зубьев при работе под нагрузкой в результате температурных деформаций деталей передачи, а также для размещения слоя смазки на рабочих профилях зубьев. Боковой зазор в зацеплении необходим также для компенсации погрешностей изготовления и монтажа передачи. Он определяется в основном величиной межосевого расстояния a w передачи и толщиной s зубьев колес.

Стандартом на эвольвентные зубчатые цилиндрические передачи (ГОСТ 1643-81) установлено восемь видов допусков на боковой зазор: h, d, c, b, a, z, y, x (обозначения допусков расположены в порядке возрастания величины допуска). Принятая величина гарантированного бокового зазора является основой для назначения вида сопряжения зубчатых колес. Этим же стандартом предусмотрено шесть видов сопряжения: H– нулевой зазор, E – малый зазор, C и D – уменьшенный зазор, B – нормальный зазор, A – увеличенный зазор. Сопряжения видов Н, Е и С требуют повышенной точности изготовления зубьев колес. Их применяют для реверсируемых передач при высоких требованиях к кинематической точности передачи, а также при наличии крутильных колебаний валов передачи. Чаще всего в среднем машиностроении используют передачи с видами сопряжения В и С. При отсутствии специальных требований к зубчатой передаче с каждым видом сопряжения употребляется определенный вид допуска на боковой зазор, обозначаемый строчной буквой, аналогичной букве вида сопряжения (например, А– а, В – в, С – с и т. д.).

Поле допуска на измерительный размер зубчатого колеса всегда направлено в тело зуба, поэтому предельные отклонения измерительного размера (верхнее и нижнее) всегда имеют отрицательные значения .

Исходные данные и замеры

На практике перед инженерами часто встает задача определения модуля реально существующей шестерни для ее ремонта или замены. При этом случается и так, что конструкторской документации на эту деталь, как и на весь механизм, в который она входит, обнаружить не удается.

Самый простой метод — метод обкатки. Берут шестерню, для которой характеристики известны. Вставляют ее в зубья тестируемой детали и пробуют обкатать вокруг. Если пара вошла в зацепление — значит их шаг совпадает. Если нет — продолжают подбор. Для косозубой выбирают подходящую по шагу фрезу.

Такой эмпирический метод неплохо срабатывает для зубчатых колес малых размеров.

Для крупных, весящих десятки, а то и сотни килограмм, такой способ физически нереализуем.

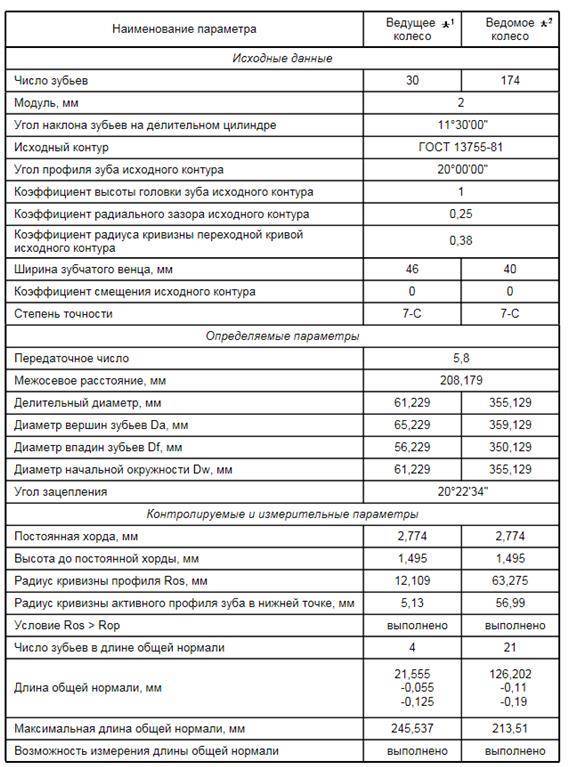
Результаты расчетов

Для более крупных потребуются измерения и вычисления.

Как известно, модуль равен диаметру окружности выступов, отнесенному к числу зубов плюс два:

m=De/(z+2)

Последовательность действий следующая:

• измерить диаметр штангенциркулем;
• сосчитать зубцы;
• разделить диаметр на z+2;
• округлить результат до ближайшего целого числа.

Зубец колеса и его параметры

Данный метод подходит как для прямозубых колес, так и для косозубых.

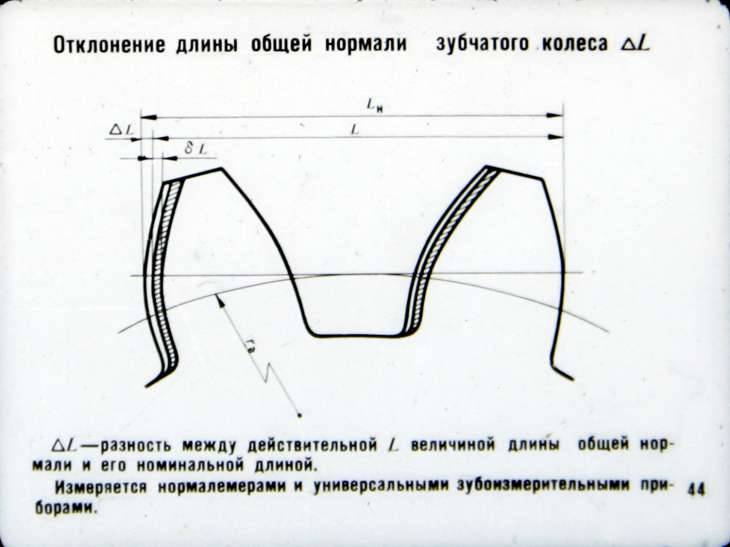
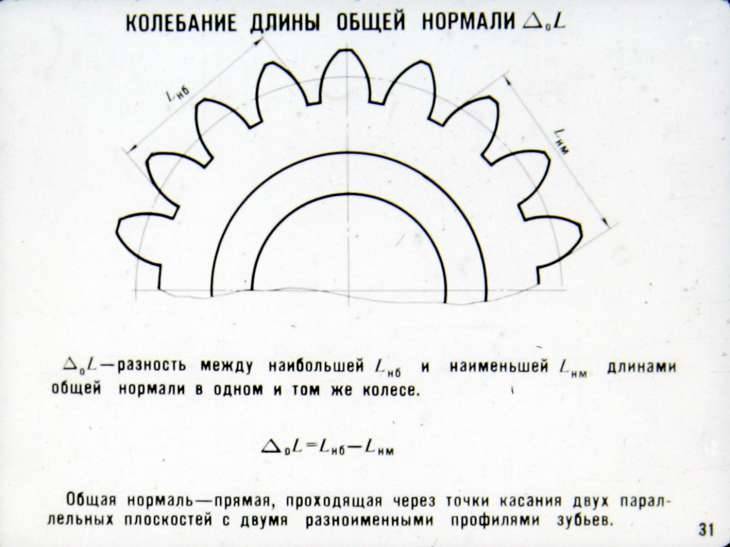
Колебание – длина – общая нормаль

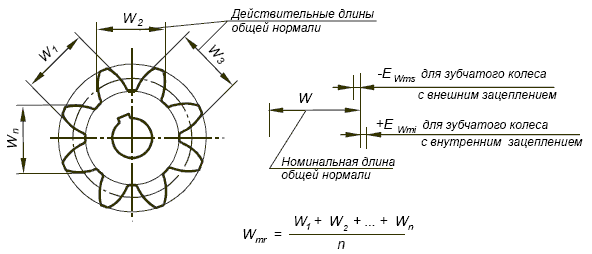
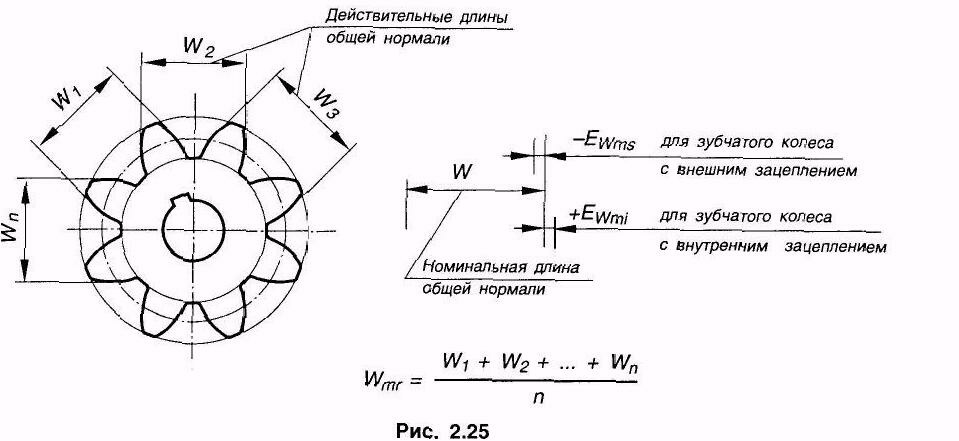
Колебание длины общей нормали ( Д0Ь) определяется разностью между наибольшей и наименьшей длиной общей нормали, полученной при измерении ее по всей окружности проверяемого зубчатого колеса.   Колебание длины общей нормали ( по окружности колеса) определяют как разность между наибольшей и наименьшей длиной нормали (

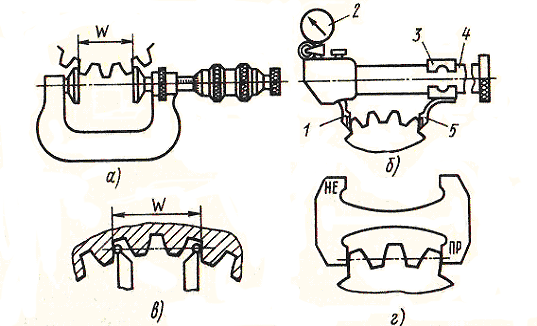
Колебание длины общей нормали L контролируют на приборах, имеющих два наконечника с параллельными плоскостями и в за-ьиеимости от требуемой точности отсчетное нониусное, микрометрическое 2 или индикаторное устройство. Особенностью контроля длины общей нормали является отсутствие необходимости базирования колеса по его оси.  

Колебание длины общей нормали L контролируют на приборах, имеющих два наконечника о параллельными плоскостями и в зависимости от требуемой точности отсчетное нониусное, микрометрическое 2 или индикаторное устройство. Особенностью контроля длины общей нормали является отсутствие необходимости базирования колеса по его оси.  

Колебание длины общей нормали Va r можно контролировать разным инструментом, у которого имеются две параллельные измерительные плоскости.  

Колебание длины общей нормали F находят как разность между наибольшей и наименьшей действительными длинами общей нормали при последовательном измерении всех групп зубьев проверяемого колеса. Колебание длины общей нормали может быть показателем погрешности обката при зубообразовании.  

Кривая накопленной погрешности шага.

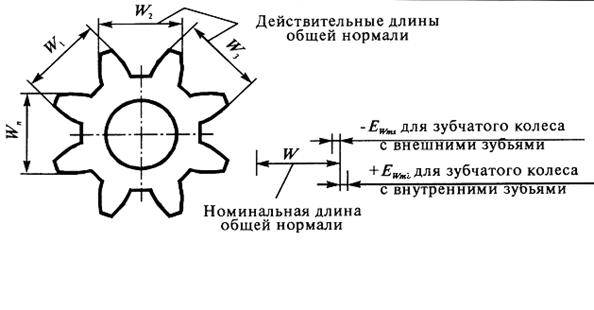
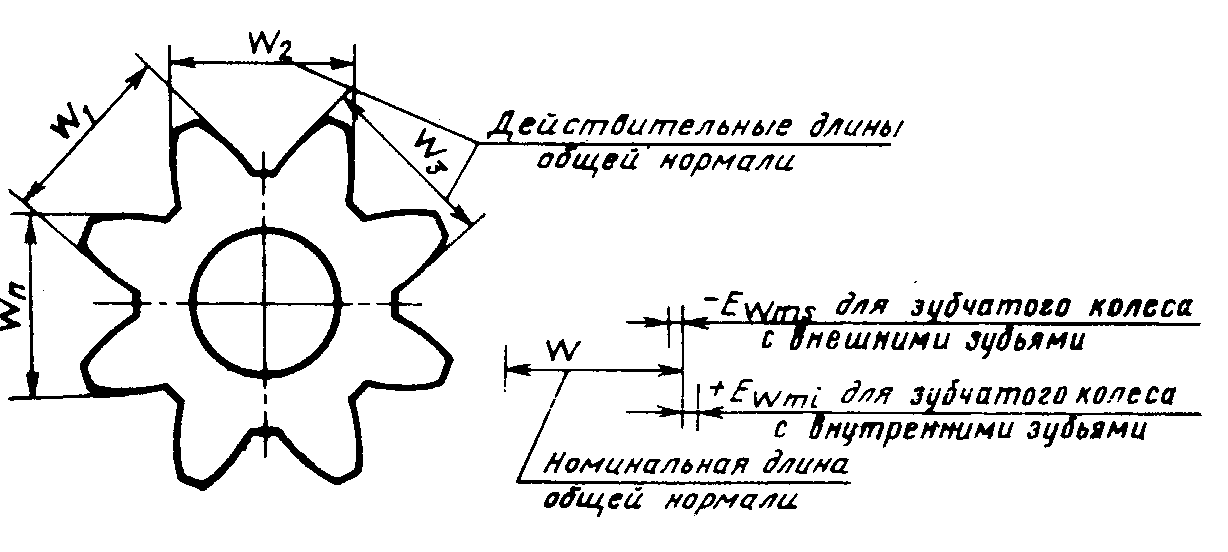
Колебанием длины общей нормали FVWr называется расстояние между двумя параллельными плоскостями касательными к двум разноименным активным боковым поверхностям зубьев зубчатого колеса.  

На колебание длины общей нормали влияют лишь тангенциальные составляющие погрешности окружных шагов и не влияют радиальные. Поэтому для полной оценки колеса в отношении кинематической точности необходимо проконтролировать колесо и по одному из параметров, учитывающих радиальные составляющие погрешностей окружных шагов, например измерить радиальное биение.  

Кривая накопленной погрешности шага.

Измерение колебания длины общей нормали проводится любым прибором, имеющим измерительные поверхности в виде параллельных плоскостей, например штангенциркулями.  

Контроль колебания длины общей нормали производится на станковых приборах, имеющих специальные приспособления, или накладными – нормалемерами и микрометрическими скобами для зубчатых колес.  

Величина колебания длины общей нормали 1UL определяется как разность наибольшей и наименьшей длины общей нормали при последовательном измерении всех групп зубьев по окружности колеса. В этом случае настройки по блоку плиток не требуется.  

Контроль колебания длины общей нормали прост и не требует иметь какой-либо промежуточной измерительной базы. Часто производится измерение длины общей нормали, а не ее колебания. Это осуществляется с целью выяснения толщины зуба и рассматривается ниже.  

Контроль колебания длины общей нормали может осуществляться с помощью микрометров ( фиг. Кирове ( КРИН), у которых в отличие от обычного микрометра имеются тарельчатые измерительные поверхности. Недостатком микрометров является то, что одна измерительная поверхность вращается и при соприкосновении с контролируемой поверхностью несколько увлекает весь прибор. Для контроля колебаний длины общей нормали более удобен прибор конструкции завода ЛИЗ ( фиг. Для колес средних размеров контроль колебания длины общей нормали удобно производить с помощью индикаторных скоб ( фиг.  

Конструкция зубчатого колеса

Несмотря на кажущуюся простоту, в технике принято выделять несколько отдельных частей зубчатого колеса. Как и любое другое колесо, зубчатый вариант в своей основе имеет диск необходимого диаметра. Основной частью является обод, на боковой или торцевой поверхности которого выполнены зубья. Все вместе они образуют так называемый венец зубчатого колеса. Геометрия зубьев различна у разных типов зубчатой передачи. Сам зуб условно разбивается на несколько частей. Наружная часть называется вершиной. Прилегающие к ней боковые поверхности носят название головки зуба. Внутренняя часть именуется ножкой зуба. Две соседние ножки образуют впадину зубчатого колеса.

Для крепления на валу механизма в центре диска изготавливается ступица со сквозным отверстием. Форма отверстия зависит от геометрии сечения вала и может быть цилиндрической, квадратной или многоугольной. При использовании цилиндрических валов, в ступице обычно выполняют шпоночный паз.

С целью уменьшения веса толщина диска колеса выполняется обычно меньше, чем толщина ступицы или обода. Также для этого в теле диска могут присутствовать окна разнообразной формы.

Стандартизация

В соответствии с принципом взаимозаменяемости ряд геометрических параметров эвольвентного зацепления стандартизован. В России зубчатые колёса выбирают по числу зубьев и модулю , принимая следующие параметры за постоянные (по ГОСТ 13755-81):

1. высота головок зуба ;
2. высота ножки зуба ;
3. подрезания нет, то есть или угол зацепления равен основному углу зацепления ;
4. угол зацепления  °;
5. коэффициент высоты головки зуба ;
6. коэффициент радиального зазора .

В США и Великобритании вместо модуля используется питч , Питч — величина обратная модулю.

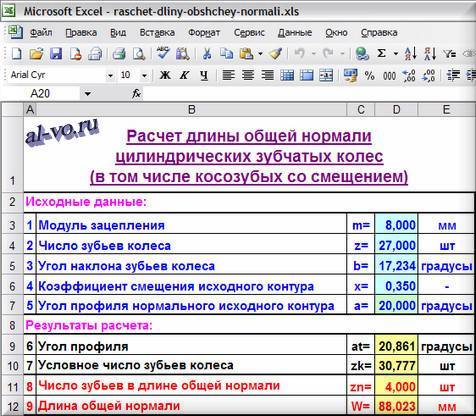
Открываем таблицу файла Excel и записываем исходные данные:  

1. Констатируем в объединенной ячейке D3E3, что параметры нормального исходного контура, участвующие в расчете, взяты по ГОСТ 13755-82. В примечании к объединенной ячейке D3E3 указано: угол исходного профиля a=20 градусов; коэффициент высоты головки зуба ha*=1; коэффициент радиального зазора c*=0,25.

2. Тип зацепления T (смотри примечание: T=1 – наружное; T=-1 – внутреннее зацепление) указываем

в  объединенной ячейке D4E4: 1

3. Модуль зацепления mв миллиметрах (в примечании – стандартный ряд модулей) вписываем

в  объединенную ячейку D5E5: 1,5

4. Угол наклона зубьев b в градусах (в примечании – рекомендации по назначению) вписываем

в  объединенную ячейку D6E6: 13,3222

5. Число зубьев z1 иz2 заносим соответственно

в  ячейку D7: 18

и в ячейку E7: 73

6.1. Далее, если известно из предыдущих расчетов межосевое расстояниеaw, то вписываем это значение в миллиметрах

в объединенную ячейку D9E9: _____

Если значение aw не известно, то оставляем ячейку D9E9 пустой! (В примере межосевое расстояние  не определено.)

6.2. Если заданы коэффициенты смещения исходного контураx1 иx2 (и соответственно не задано aw!), то вписываем эти значения

в  ячейку D10: 0,300

и в ячейку E10: 0,300

Если значения x1 иx2 не заданы, то ничего не записываем в ячейки D10 и E10!

Почему, как и зачем назначать смещение исходного контура, выполняя геометрический расчет зубчатой передачи, мы постараемся обсудить на страницах блога (при наличии интереса аудитории) в статьях, которые будут опубликованы в  будущем.

Чтобы не пропустить выход статей, получайте анонсы. Для этого необходимо в окне, расположенном вверху страницы. Введите адрес своей электронной почты и нажмите на кнопку «Получать анонсы статей», подтвердитеподпискув письме, которое тут же придет к вам на указанную почту!

Применение

Высокие свойства зубчатых передач нашли отражение в широком спектре применений. Во многих промышленных механизмах используются редукторы, призванные понизить  число оборотов вращения вала двигателя, для передачи на технологическое оборудование. Помимо изменения скорости, такое устройство также увеличивает механический момент. В итоге маломощный двигатель с большой скоростью вращения, способен приводить в движение медленный и тяжелый механизм.

С целью уменьшения габаритов редуктора его часто выполняют многоступенчатым. Большое количество зубчатых колес входят в последовательное зацепление между собой, обеспечивая высокое передаточное число. Классическим примером подобного устройства являются обычные механические часы. Благодаря множеству специально подобранных передач, скорости движения секундной, минутной и часовой стрелок отличаются друг от друга ровно в 60 раз.

Меняя один комплект на другой, можно получить разные скорости выходного вала. Этот принцип действия лег в основу коробок переключения передач, широко используемых в автомобилестроении, станкостроении и других отраслях.

Обычное зубчатое колесо допускает применение и для повышения скорости выходного вала относительно входного. В общем случае для этого достаточно развернуть редуктор или поменять местами точки подключения двигателя и конечного механизма.  Называется подобное устройство мультипликатор. Из особенностей его применения необходимо учитывать запас по мощности двигателя, сопоставимый с передаточным числом механизма.

Зубчатые колеса используются также  для изменения направления движения. Две цилиндрические шестерни с одинаковым числом зубьев реализуют функцию смены направления вращения вала. Передачи конической или корончатой конструкции используются в случае необходимости смены положения оси в пространстве. Ведущая и ведомая шестерни в таких механизмах развернуты друг относительно друга на какой-либо угол, значение которого может достигать 90 градусов. При этом передаточное отношение часто равно единице, что обеспечивает одинаковые скорости валов.

Наряду с простыми вариантами передач, содержащих зубчатые колеса, разработаны несколько специальных моделей. С целью снижения материалоемкости, в механизмах с ограниченным углом поворота, используют только часть зубчатого колеса. Такой сектор, обладая всеми основными свойствами зубчатого зацепления, отличается более низкой  массой и стоимостью.

Еще один вариант, называемый планетарной передачей, также характеризуется малым весом и габаритами. При этом устройство обеспечивает высокое значение передаточного числа и пониженный уровень шума в процессе работы. Конструктивно такая передача состоит из нескольких шестерен, имеющих разную степень свободы. За счет этого механизм может не только передавать вращение, но и складывать или выделять угловые скорости разных валов, находящихся на одной оси. Сегодня разработано большое число вариантов планетарных передач,  отличающихся типом и взаимным расположением зубчатых колес. Планетарные передачи широко применяются в автомобильной и авиационной технике, тяжелом металлорежущем оборудовании. Среди недостатков, сдерживающих распространение передач данного типа, следует отметить низкий КПД и высокие конструктивные требования к точности изготовления отдельных деталей.

1.3. Допуски на измерительные размеры цилиндрических зубчатых колес

Рассмотренные выше формулы для вычисления номинальных измерительных размеров цилиндрических зубчатых колес гарантируют беззазорное зацепление колес в передаче. В реальных зубчатых передачах должен быть обеспечен гарантированный боковой зазор с целью устранения заклинивания зубьев при работе под нагрузкой в результате температурных деформаций деталей передачи, а также для размещения слоя смазки на рабочих профилях зубьев. Боковой зазор в зацеплении необходим также для компенсации погрешностей изготовления и монтажа передачи. Он определяется в основном величиной межосевого расстояния a w передачи и толщиной s зубьев колес.

Стандартом на эвольвентные зубчатые цилиндрические передачи (ГОСТ 1643-81) установлено восемь видов допусков на боковой зазор: h, d, c, b, a, z, y, x (обозначения допусков расположены в порядке возрастания величины допуска). Принятая величина гарантированного бокового зазора является основой для назначения вида сопряжения зубчатых колес. Этим же стандартом предусмотрено шесть видов сопряжения: H– нулевой зазор, E – малый зазор, C и D – уменьшенный зазор, B – нормальный зазор, A – увеличенный зазор. Сопряжения видов Н, Е и С требуют повышенной точности изготовления зубьев колес. Их применяют для реверсируемых передач при высоких требованиях к кинематической точности передачи, а также при наличии крутильных колебаний валов передачи. Чаще всего в среднем машиностроении используют передачи с видами сопряжения В и С. При отсутствии специальных требований к зубчатой передаче с каждым видом сопряжения употребляется определенный вид допуска на боковой зазор, обозначаемый строчной буквой, аналогичной букве вида сопряжения (например, А– а, В – в, С – с и т. д.).

Поле допуска на измерительный размер зубчатого колеса всегда направлено в тело зуба, поэтому предельные отклонения измерительного размера (верхнее и нижнее) всегда имеют отрицательные значения .

Заключение.

При контроле изготовленных зубчатых колес сравниваются измеренные микрометром и рассчитанные значения размеров по роликам (шарикам).

Допуски на размеры по роликам (шарикам) назначаются по ГОСТ 1643-81 в зависимости от требований к передаче.

Теме зубчатых колес на блоге посвящено еще несколько важных и, думаю, полезных статей в рубрике «Механика». Быстро найти их вы сможете в перечне на странице «Все статьи блога».

Для получения информации о выходе новых статей и для скачивания рабочих файлов программ прошу вас подписаться на анонсы в окне, расположенном в конце статьи или в окне вверху страницы.

Прошу УВАЖАЮЩИХ труд автора скачать файл ПОСЛЕ ПОДПИСКИ на анонсы статей!

Ссылка на скачивание файла: raschet-razmera-po-rolikam (xls 37.0KB).