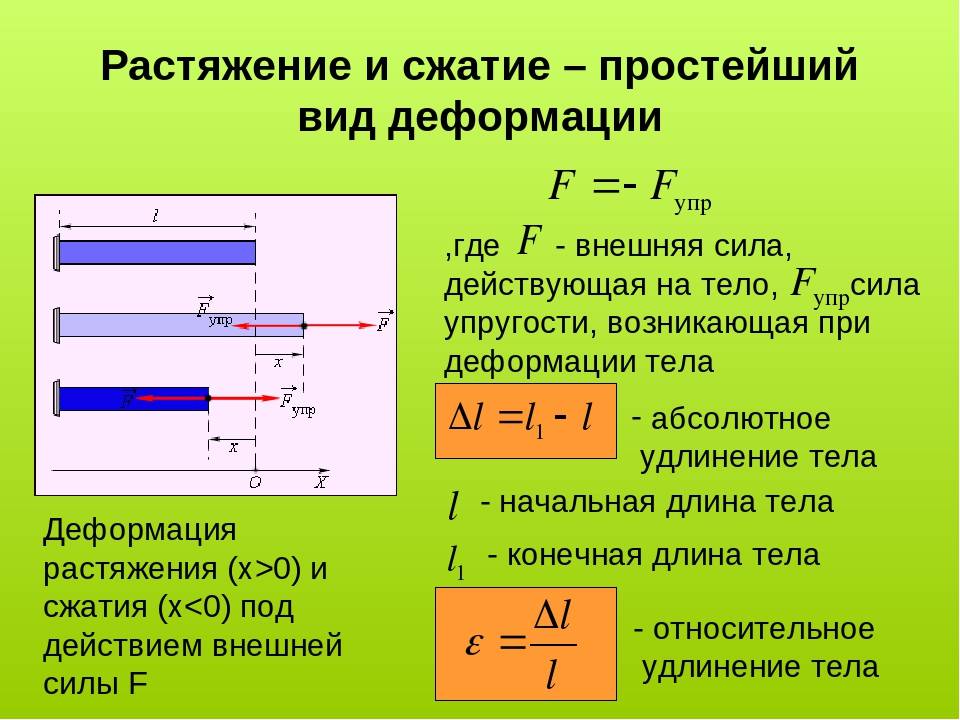
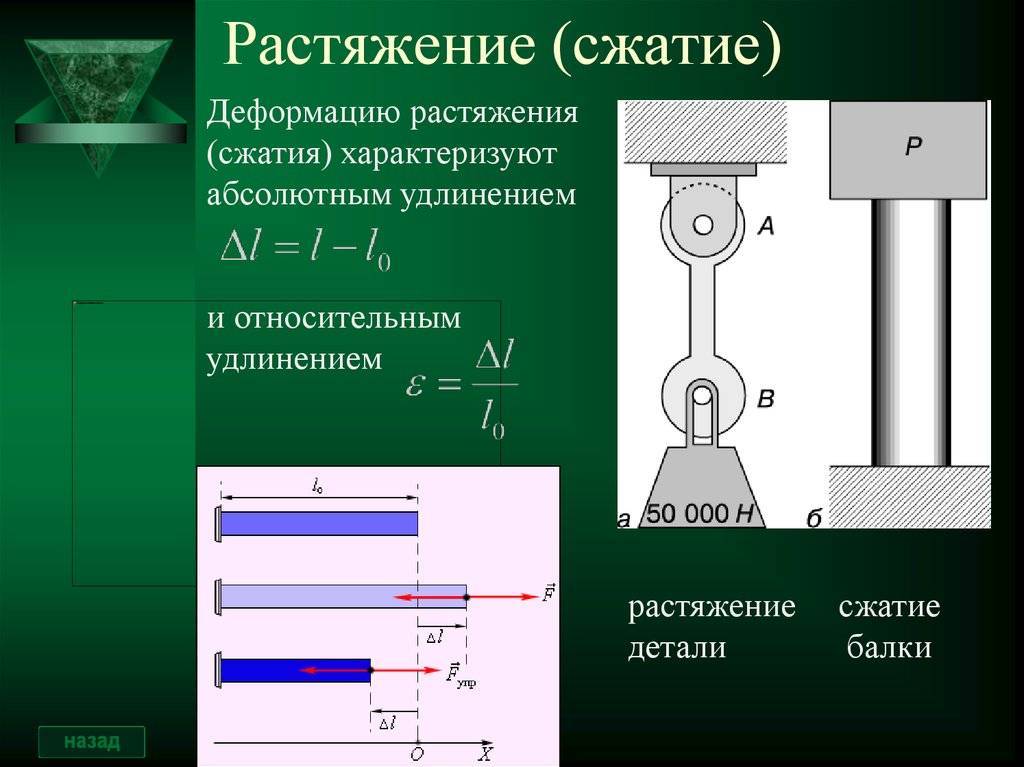
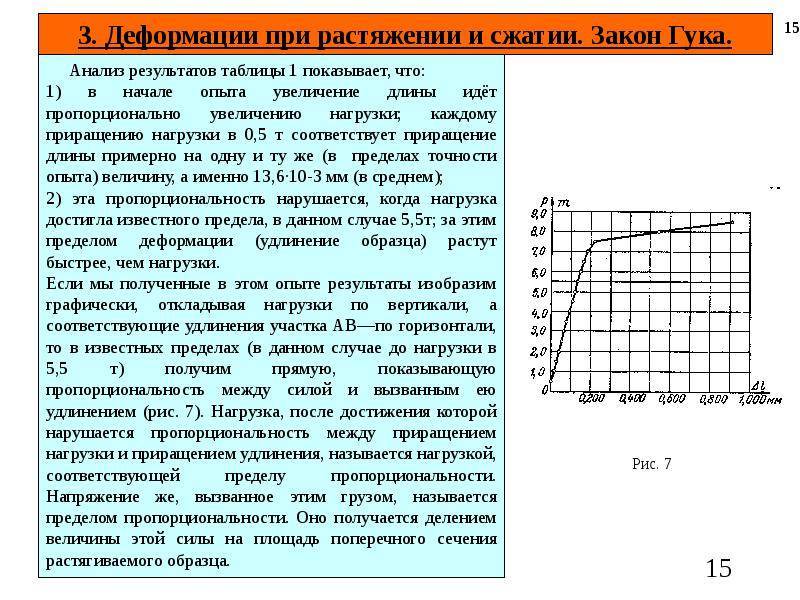
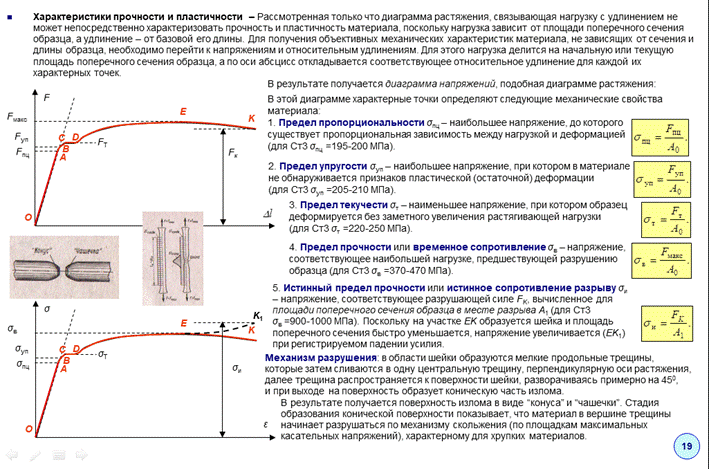
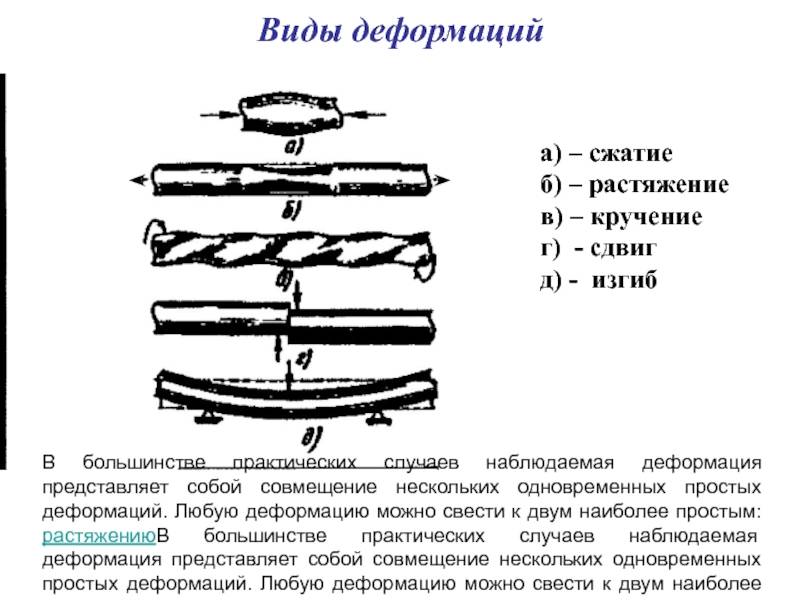
Диаграммы напряжений
На сегодняшний день существует несколько методик испытания образцов материалов. При этом одним из самых простых и показательных являются испытания на растяжение (на разрыв), позволяющие определить предел пропорциональности, предел текучести, модуль упругости и другие важные характеристики материала. Так как важнейшей характеристикой напряженного состояния материала является деформация, то определение значения деформации при известных размерах образца и действующих на образец нагрузок позволяет установить вышеуказанные характеристики материала.
Тут может возникнуть вопрос: почему нельзя просто определить сопротивление материала? Дело в том, что абсолютно упругие материалы, разрушающиеся только после преодоления некоторого предела – сопротивления, существуют только в теории. В реальности большинство материалов обладают как упругими так и пластическими свойствами, что это за свойства, рассмотрим ниже на примере металлов.
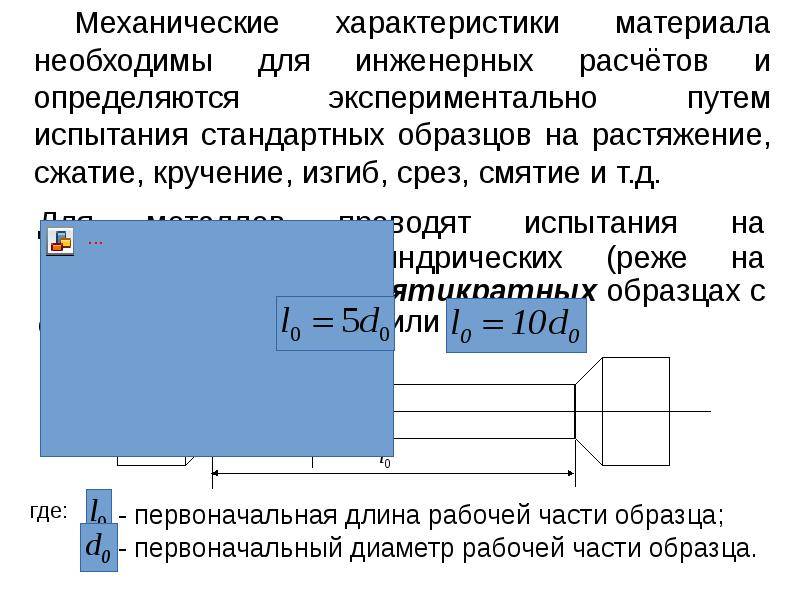
Испытания металлов на растяжение проводятся согласно ГОСТ 1497-84. Для этого используются стандартные образцы. Методика испытаний выглядит приблизительно так: к образцу прикладывается статическая нагрузка, определяется абсолютное удлинение образца Δl, затем нагрузка увеличивается на некоторое шаговое значение и снова определяется абсолютное удлинение образца и так далее. На основании полученных данных строится график зависимости удлинений от нагрузки. Этот график называется диаграммой напряжений.
Рисунок 318.1. Диаграмма напряжений для стального образца.
На данной диаграмме мы видим 5 характерных точек:
1. Предел пропорциональности Рп (точка А)
Нормальные напряжения в поперечном сечении образца при достижении предела пропорциональности будут равны:
σп = Рп/Fo (318.2.1)
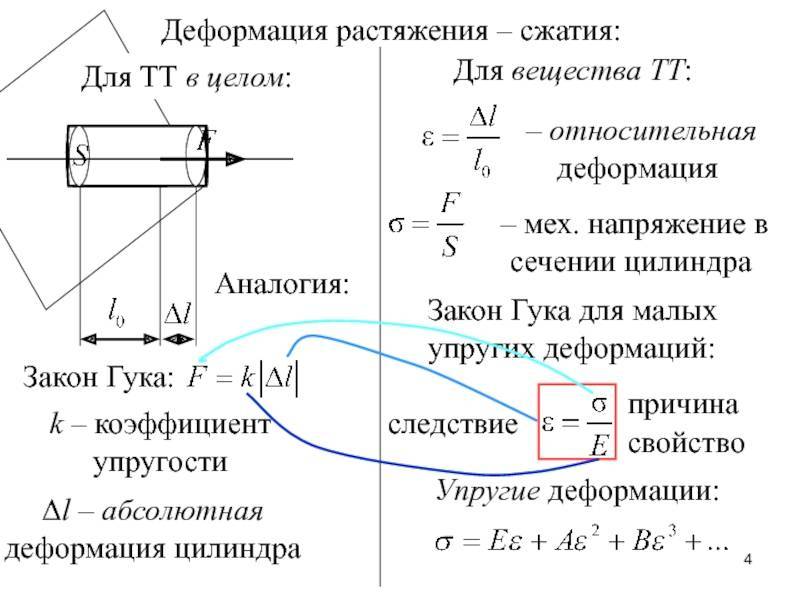
Предел пропорциональности ограничивает участок упругих деформаций на диаграмме. На этом участке деформации прямо пропорциональны напряжениям, что выражается законом Гука:
Рп = kΔl (318.2.2)
где k – коэффициент жесткости:
k = EF/l (318.2.3)
где l – длина образца, F – площадь сечения, Е – модуль Юнга.
Влияние радиоактивного облучения на изменение механических свойств
Радиоактивное облучение по-разному влияет на различные материалы. Облучение материалов неорганического происхождения по своему влиянию на механические характеристики и характеристики пластичности подобно понижению температуры: с увеличением дозы радиоактивного облучения увеличивается предел прочности и особенно предел текучести, а характеристики пластичности снижаются.
Облучение пластмасс также приводит к увеличению хрупкости, причем на предел прочности этих материалов облучение оказывает различное влияние: на некоторых пластмассах оно почти не сказывается (полиэтилен), у других вызывает значительное понижение предела прочности (катамен), а в третьих – повышение предела прочности (селектрон).
Лекция 3. Методики расчета конструкций.
Примеры деформации разных видов
1. Играем на гитаре — кратковременно растягиваем струны
2. Садимся в автомобиль — пружины подвески сжимаются
3. Сидим на тонкой доске — доска прогибается
4. Затягиваем шуруп — происходит кручение отвёртки (хоть мы и не видим деформацию отвёртки)
5. Двигаем расшатанный стул — происходит сдвиг сиденья относительно пола
{"questions":,"explanations":,"answer":}},"hints":},{"content":"Какому виду деформации подвергается мяч при ударе?`choice-7`","widgets":{"choice-7":{"type":"choice","options":,"explanations":,"answer":}},"hints":},{"content":"Упругую дощечку сломали пополам. Какой вид деформации произошёл?`choice-16`","widgets":{"choice-16":{"type":"choice","options":,"explanations":,"answer":}},"hints":}]}Внутренние усилия при растяжении и сжатии
При приложении к брусу с постоянным сечением внешних воздействий, действие которых в любом поперечном разрезе направлено параллельно его центральной оси и перпендикулярно сечению, с ним происходит следующий вид деформации: растяжение или сжатие. На основе гипотезы о принципе независимости внешнего воздействия для каждого из поперечных разрезов можно рассчитать внутреннее усилие как векторную сумму всех приложенных внешних воздействий. Растягивающие нагрузки в сопромате принято считать положительными, а сжимающие отрицательными.
Рассмотрев произвольный разрез бруса или стержня, можно сказать что внутренние напряжения равны векторной сумме всех внешних сил, сгруппированных по одной из его сторон. Это верно только с учетом принципа Сен-Венана (фр. инженер А. Сен-Венан, 1797-1886) о смягчении граничных условий, т.к. распределение внутренних усилий по поверхности разреза носит сложный характер с нелинейными зависимостями, но в данном случае значением погрешности можно пренебречь как несущественным.
Применяя гипотезу Бернулли (швейцарский математик, И. Бернулли, 1667-1748) о плоских сечениях, для более наглядного представления процессов распределения сил и напряжений по центральной оси бруса можно построить эпюры. Визуальное представление более информативно и в некоторых случаях позволяет получить необходимые величины без сложных расчетов. Графическое представление отражает наиболее нагруженные участки стержня, инженер может сразу определить проблемные места и ограничиться расчетами только для критических точек.

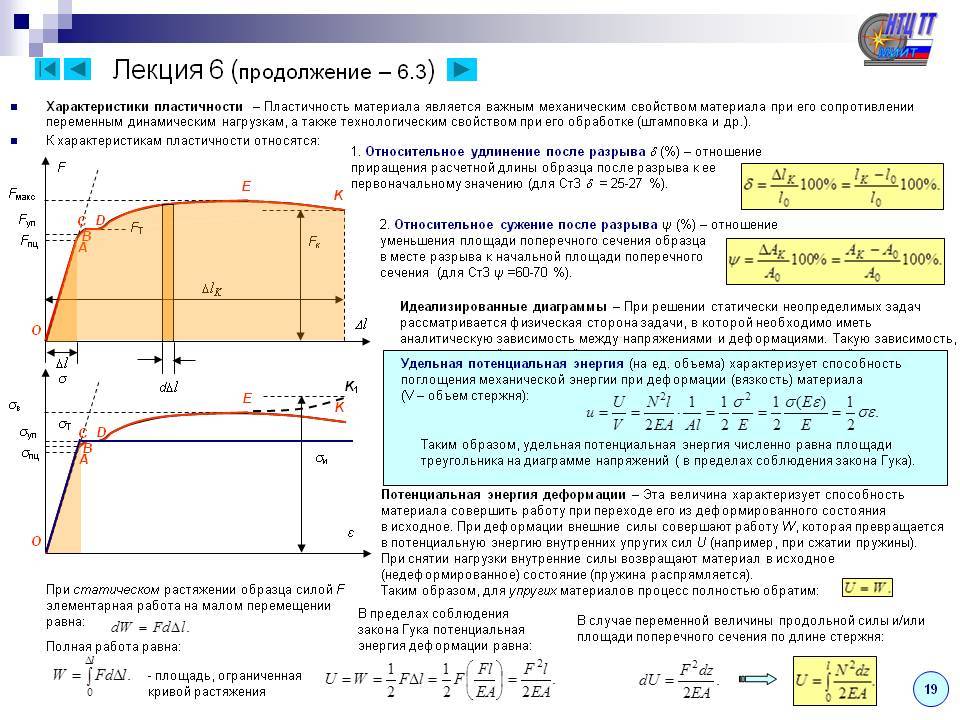
Все вышесказанное может быть применимо при квазистатической (система может быть описана статически) нагрузке стержня с постоянным диаметром. Потенциальная энергия системы на примере растяжения стержня определяется по формуле:
U=W=FΔl/2=N²l/(2EA)
Потенциальная энергия растяжения U концентрируется в образце и может быть приравнена к выполнению работы W (незначительное выделение тепловой энергии можно отнести к погрешности), которая была произведена силой F для увеличения длины стержня на значение абсолютного удлинения. Преобразуя формулу, получаем, что вычислить значение величины потенциальной энергии растяжения можно, рассчитав отношение квадрата продольной силы N помноженной на длину стержня l и удвоенного произведения модуля Юнга E материала на величину сечения A.
Как видно из формулы, энергия растяжения всегда носит положительное значение, для нее невозможно применить гипотезу о независимости действия сил, т.к. это не векторная величина. Единица измерения – джоуль (Дж). В нижней части формулы стоит произведение EA – это так называемая жесткость сечения, при неизменном модуле Юнга она растет только за счет увеличения площади. Величина отношения жесткости к длине бруса рассматривается как жесткость бруса целиком.
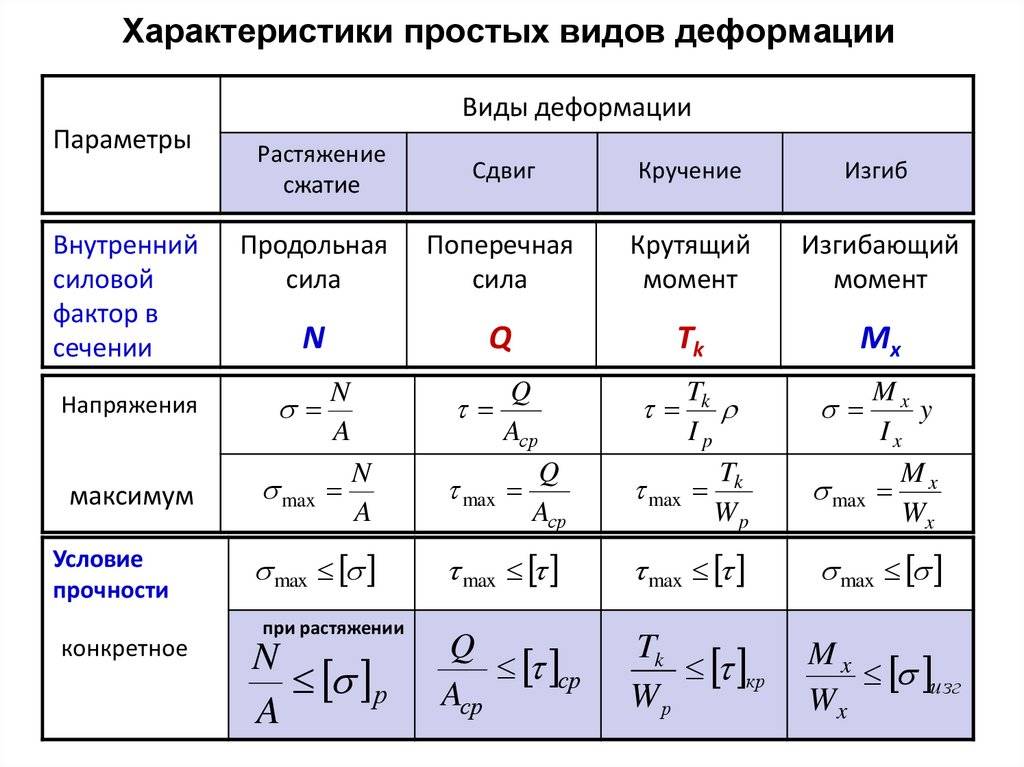
Типы деформации
В зависимости от того, как приложена внешняя сила, различают деформации растяжения-сжатия, сдвига, изгиба, кручения.
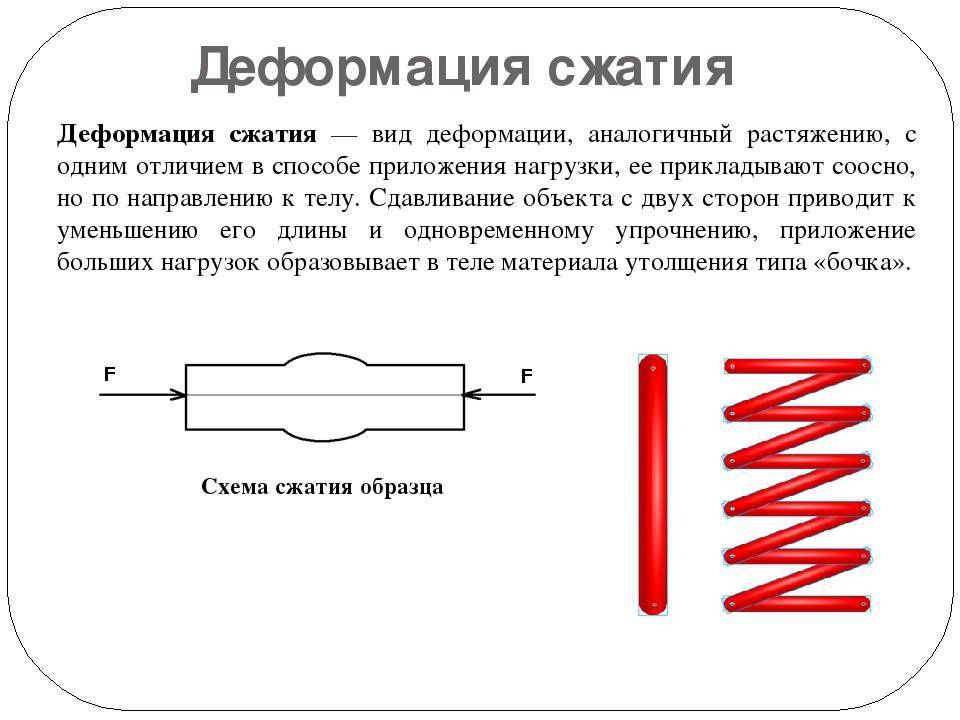
Деформация растяжения-сжатия
Деформация растяжения-сжатия вызывается силами, которые приложены к концам бруса параллельно его продольной оси и направлены в разные стороны.
Под действием внешних сил частицы твёрдого вещества, колеблющиеся относительно своего положения равновесия, смещаются. Но этому процессу пытаются помешать внутренние силы взаимодействия между частицами, старающиеся удержать их в исходном положении на определённом расстоянии друг от друга. Силы, препятствующие деформации, называются силами упругости.
Деформацию растяжения испытывают натянутая тетива лука, буксировочный трос автомобиля при буксировке, сцепные устройства железнодорожных вагонов и др.
Когда мы поднимается по лестнице, ступеньки под действием нашей силы тяжести деформируются. Это деформация сжатия. Такую же деформацию испытывают фундаменты зданий, колонны, стены, шест, с которым прыгает спортсмен.
Деформация сдвига
Если приложить внешнюю силу по касательной к поверхности бруска, нижняя часть которого закреплена, то возникает деформация сдвига. В этом случае параллельные слои тела как бы сдвигаются относительно друг друга.
Представим себе расшатанный табурет, стоящий на полу. Приложим к нему силу по касательной к его поверхности, то есть, попросту потянем верхнюю часть табурета на себя. Все его плоскости, параллельные полу, сместятся друг относительно друга на одинаковый угол.
Такая же деформация происходит, когда лист бумаги разрезается ножницами, пилой с острыми зубьями распиливается деревянный брус и др. Деформации сдвига подвергаются все крепёжные детали, соединяющие поверхности, – винты, гайки и др.
Влияние радиоактивного облучения на изменение механических свойств
Радиоактивное облучение по-разному влияет на различные материалы. Облучение материалов неорганического происхождения по своему влиянию на механические характеристики и характеристики пластичности подобно понижению температуры: с увеличением дозы радиоактивного облучения увеличивается предел прочности и особенно предел текучести, а характеристики пластичности снижаются.
Облучение пластмасс также приводит к увеличению хрупкости, причем на предел прочности этих материалов облучение оказывает различное влияние: на некоторых пластмассах оно почти не сказывается (полиэтилен), у других вызывает значительное понижение предела прочности (катамен), а в третьих — повышение предела прочности (селектрон).
для теплоустойчивых хромистых сталей
12XM, 12MX, 15XM, 15X5M, 15X5M-У:
- При расчетных температурах ниже 20 °С допускаемые напряжения принимают такими же, как при 20 °С при условии допустимого применения материала при данной температуре.
- Для промежуточных расчетных температур стенки допускаемое напряжение определяют линейной интерполяцией с округлением результатов до 0,5 МПа в сторону меньшего значения.
- Допускаемые напряжения, расположенные ниже горизонтальной черты, действительны при ресурсе 105 ч. Для расчетного срока эксплуатации до 2*105 ч допускаемое напряжение, расположенное ниже горизонтальной черты, умножают на коэффициент 0,85.
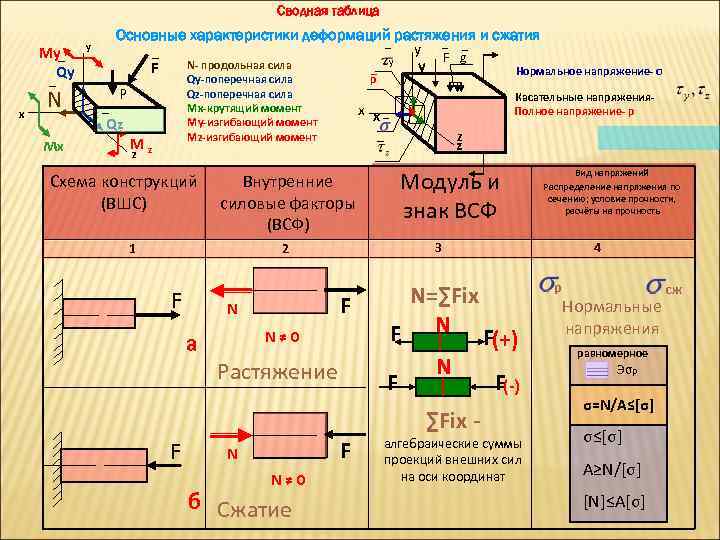
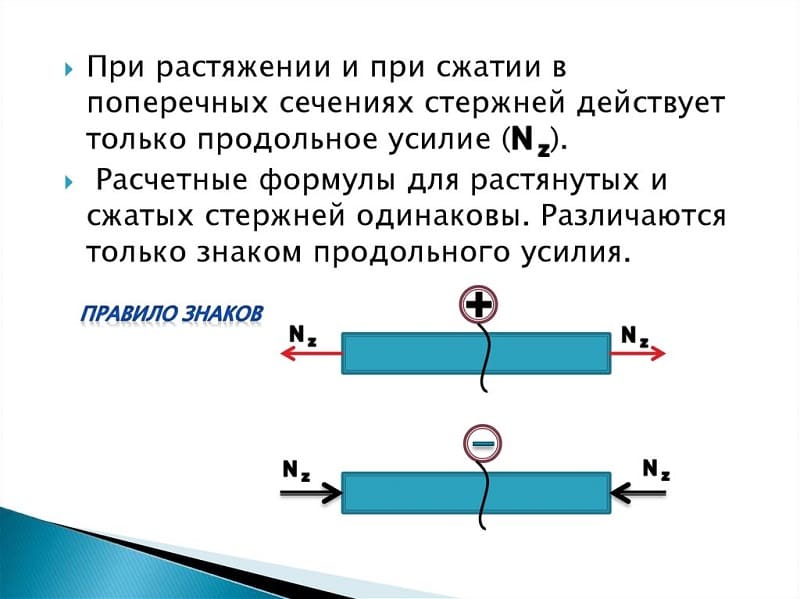
Внутренние усилия при растяжении-сжатии.
Осевое (центральное) растяжение или сжатие прямого бруса вызывается внешними силами, вектор равнодействующей которых совпадает с осью бруса. При растяжении или сжатии в поперечных сечениях бруса возникают только продольные силы N. Продольная сила N в некотором сечении равна алгебраической сумме проекции на ось стержня всех внешних сил, действующих по одну сторону от рассматриваемого сечения. По правилу знаков продольной силы N принято считать, что от растягивающих внешних нагрузок возникают положительные продольные силы N, а от сжимающих — продольные силы N отрицательны (рис. 5). Чтобы выявить участки стержня или его сечения, где продольная сила имеет наибольшее значение, строят эпюру продольных сил, применяя метод сечений, подробно рассмотренный в статье: Анализ внутренних силовых факторов в статистически определимых системах Ещё настоятельно рекомендую взглянуть на статью: Расчёт статистически определимого бруса Если разберёте теорию в данной статье и задачи по ссылкам, то станете гуру в теме «Растяжение-сжатие» =)
Формулы и способы расчета пружин из стали круглого сечения по ГОСТ 13765
Пружина сжатия Пружина растяжения
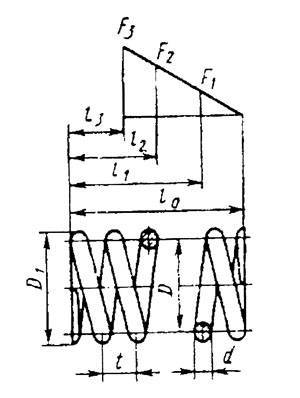

| Наименование параметра | Обозначение | Расчетные формулы и значения | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Сила пружины при предварительной деформации, Н | F 1 | Принимается в зависимости от нагрузки пружины | ||||||||||||||
| Сила пружины при рабочей деформации (соответствует наибольшему принудительному перемещению подвижного звена в механизме), Н | F 3 | Принимается в зависимости от нагрузки пружины | ||||||||||||||
| Рабочий ход пружины, мм | h | Принимается в зависимости от нагрузки пружины | ||||||||||||||
| Наибольшая скорость перемещения подвижного конца пружины при нагружении или разгрузке, м/с | v max | Принимается в зависимости от нагрузки пружины | ||||||||||||||
| Выносливость пружины, число циклов до разрушения | N F | Принимается в зависимости от нагрузки пружины | ||||||||||||||
| Наружный диаметр пружины, мм | D 1 | Предварительно принимаются с учетом конструкции узла. Уточняются по таблицам ГОСТ 13766…ГОСТ 13776 | ||||||||||||||
| Относительный инерционный зазор пружины сжатия. Для пружин растяжения служит ограничением максимальной деформации | δ | δ = 1 — F 2 / F 3 (1) Для пружин сжатия классов I и II δ = 0,05 — 0,25 для пружин растяжения δ = 0,05 — 0,10 для одножильных пружин класса III δ = 0,10 — 0,40 для трехжильных класса III δ = 0,15 — 0,40 | ||||||||||||||
| Сила пружины при максимальной деформации, Н | F 3 | Уточняется по таблицам ГОСТ 13766 ÷ ГОСТ 13776 | ||||||||||||||
| Сила предварительного напряжения (при навивке из холоднотянутой и термообработанной проволоки), Н | F | (0,1 ÷ 0,25) F 3 | ||||||||||||||
| Диаметр проволоки, мм | d | Выбирается по таблицам ГОСТ 13764 ÷ ГОСТ 13776 | ||||||||||||||
| Диаметр трехжильного троса, мм | d 1 | Выбирается по таблицам ГОСТ 13764 ÷ ГОСТ 13776 | ||||||||||||||
| Жесткость одного витка пружины, Н/мм | c 1 | Выбирается по таблицам ГОСТ 13764 ÷ ГОСТ 13776 | ||||||||||||||
| Максимальная деформация одного витка пружины, мм | s’ (при F = 0) s» (при F > 0) | Выбирается по таблицам ГОСТ 13764 ÷ ГОСТ 13776 | ||||||||||||||
| Максимальное касательное напряжение пружины, МПа | τ 3 | Для трехжильных пружин | ||||||||||||||
| Критическая скорость пружины сжатия, м/с | v k | Для трехжильных пружин | ||||||||||||||
| Модуль сдвига, МПа | G | Для пружинной сталиG = 7,85 х 104 | ||||||||||||||
| Динамическая (гравитационная) плотность материала, Н • с2/м4 | ρ | ρ = γ / g, где g — ускорение свободного падения, м/с2 γ — удельный вес, Н/м3 Для пружинной стали ρ = 8•103 | ||||||||||||||
| Жесткость пружины, Н/мм | с | Для пружин с предварительным напряжением Для трехжильных пружин | ||||||||||||||
| Число рабочих витков пружины | n | |||||||||||||||
| Полное число витков пружины | n 1 | где n2 — число опорных витков | ||||||||||||||
| Средний диаметр пружины, мм | D | Для трехжильных пружин | ||||||||||||||
| Индекс пружины | i | Для трехжильных пружин Рекомендуется назначать от 4 до 12 | ||||||||||||||
| Коэффициент расплющивания троса в трехжильной пружине, учитывающий увеличение сечения витка вдоль оси пружины после навивки | Δ | Для трехжильного троса с углом свивки β = 24° определяется по таблице
| ||||||||||||||
| Предварительная деформация пружины, мм | s 1 | |||||||||||||||
| Рабочая деформация пружины, мм | s 2 | |||||||||||||||
| Максимальная деформация пружины, мм | s 3 | |||||||||||||||
| Длина пружины при максимальной деформации, мм | l 3 | где n3 — число обработанных витков Для трехжильных пружин Для пружин растяжения с зацепами | ||||||||||||||
| Длина пружины в свободном состоянии, мм | l | |||||||||||||||
| Длина пружины растяжения без зацепов в свободном состоянии, мм | l’ | |||||||||||||||
| Длина пружины при предварительной деформации, мм | l 1 | Для пружин растяжения | ||||||||||||||
| Длина пружины при рабочей деформации, мм | l 2 | Для пружин растяжения | ||||||||||||||
| Шаг пружины в свободном состоянии, мм | t | Для трехжильных пружин Для пружин растяжения | ||||||||||||||
| Напряжение в пружине при предварительной деформации, МПа | τ 1 | |||||||||||||||
| Напряжение в пружине при рабочей деформации, МПа | τ 2 | |||||||||||||||
| Коэффициент, учитывающий кривизну витка пружины | k | Для трехжильных пружин | ||||||||||||||
| Длина развернутой пружины (для пружин растяжения без зацепов), мм | l | |||||||||||||||
| Масса пружины (для пружин растяжения без зацепов), кг | m | |||||||||||||||
| Объем, занимаемый пружиной (без учета зацепов пружины), мм 3 | V | |||||||||||||||
| Зазор между концом опорного витка и соседним рабочим витком пружины сжатия, мм | λ | Устанавливается в зависимости от формы опорного витка | ||||||||||||||
| Внутренний диаметр пружины, мм | D 2 | |||||||||||||||
| Временное сопротивление проволоки при растяжении, МПа | R m | Устанавливается при испытаниях проволоки или по ГОСТ 9389 и ГОСТ 1071 | ||||||||||||||
| Максимальная энергия, накапливаемая пружиной, или работа деформации, мДж | Для пружин сжатия и растяжения без предварительного напряжения Для пружин растяжения с предварительным напряжением |
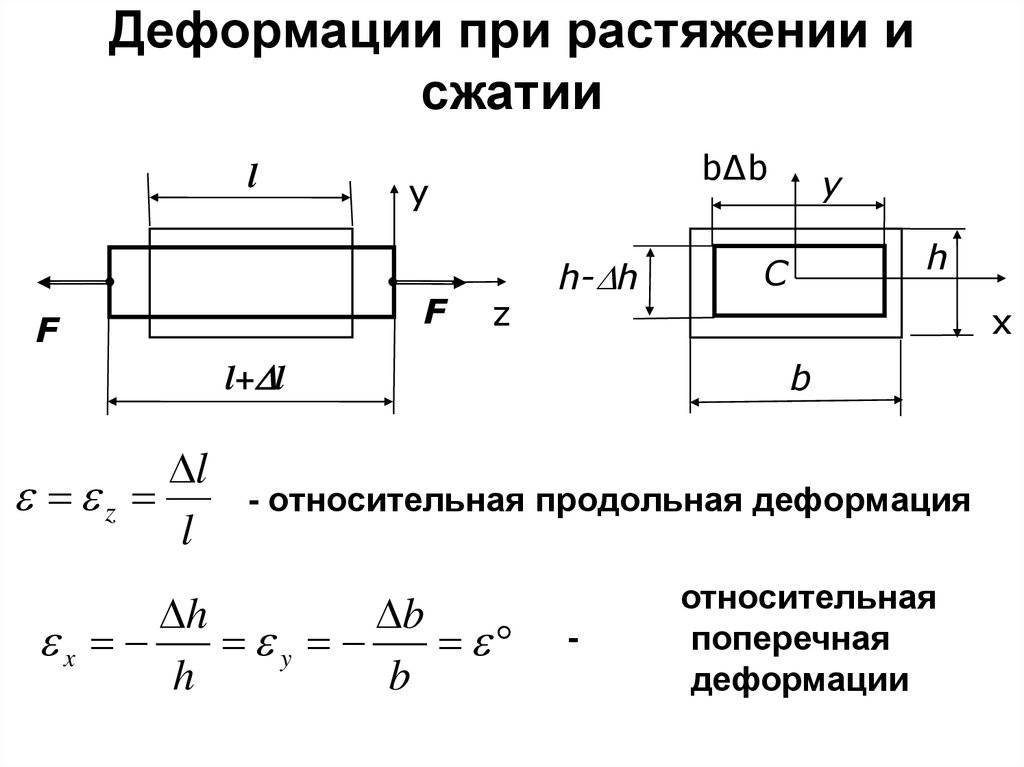
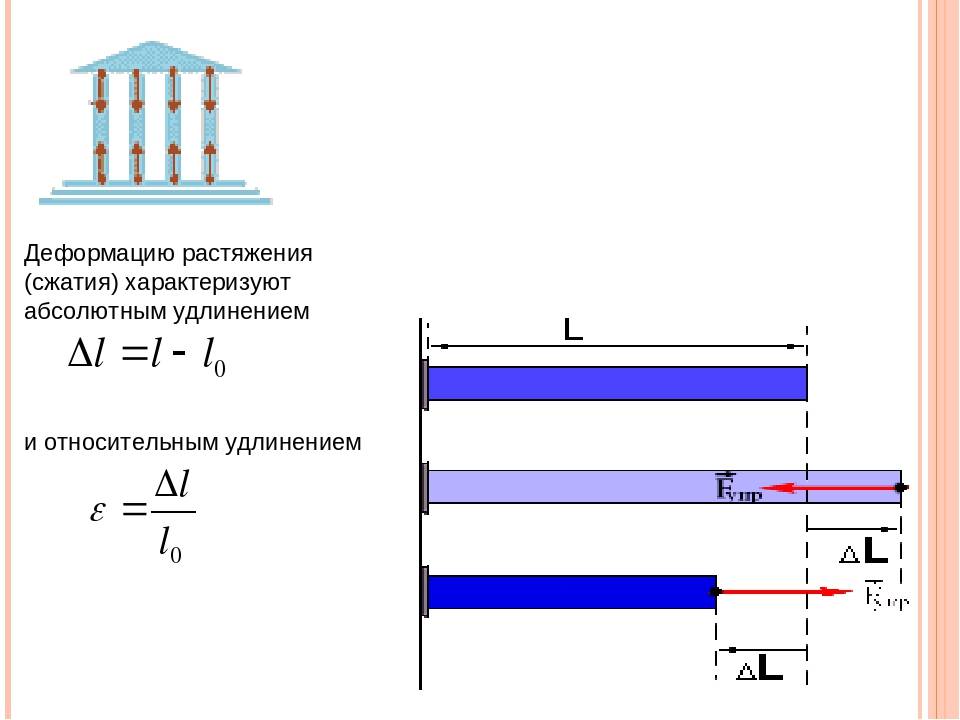
Деформации при растяжении сжатии
При растяжении/сжатии бруса могут возникать 2 вида деформации. Первый – упругая, второй – пластическая. Для упругой деформации характерно восстановление первоначальных параметров после прекращения воздействия. В случае пластической стадии деформации материала он утрачивает и не восстанавливает форму и размеры. Величина воздействия для перехода одного вида в другой называется пределом текучести.
Для расчета перемещения при растяжении бруса или стержня следует использовать метод разделения на участки, в рамках которых осуществляется приложение внешних воздействий. В точках воздействия силы следует вычислить величину изменения длины, используя формулу: Δl=Nl/EA. Как видно она зависит от жесткости сечения, длины бруса или стержня и величины действующей продольной силы. Итоговым перемещением для бруса целиком будет сумма всех частичных перемещений, рассчитанных для точек приложения силы.

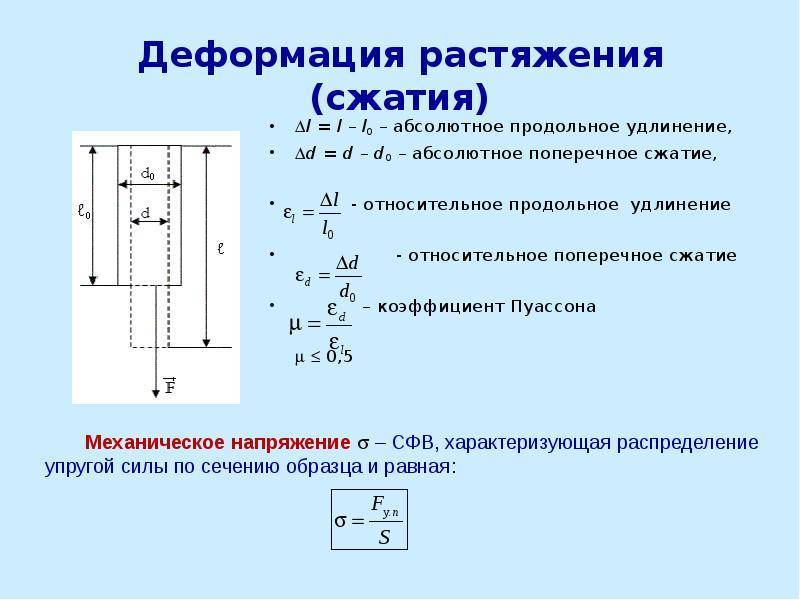
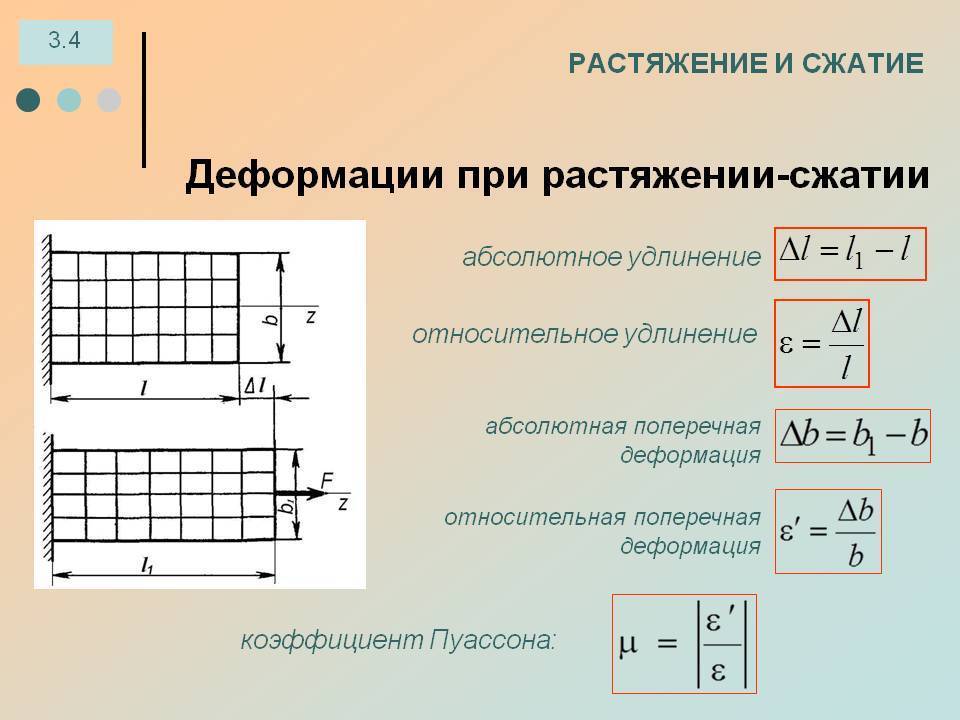
Поперечные деформации бруса (становится более толстым при сжатии и тонким при растяжении) также характеризуются абсолютной и относительной величиной деформации. Первая – разность между размером сечения после и до приложения внешних воздействий, вторая – отношение абсолютной деформации к его исходному размеру. Коэффициент Пуассона, отражающий линейную зависимость продольной и поперечной деформаций, определяет упругие качества материалов и считается неизменным для растяжения и сжатия. Продольные наиболее наглядно отражают процессы, происходящие в брусе или стержне при внешнем воздействии. Зная величину любой из них (продольной или поперечной) и используя коэффициент Пуассона, можно рассчитать значение неизвестной.
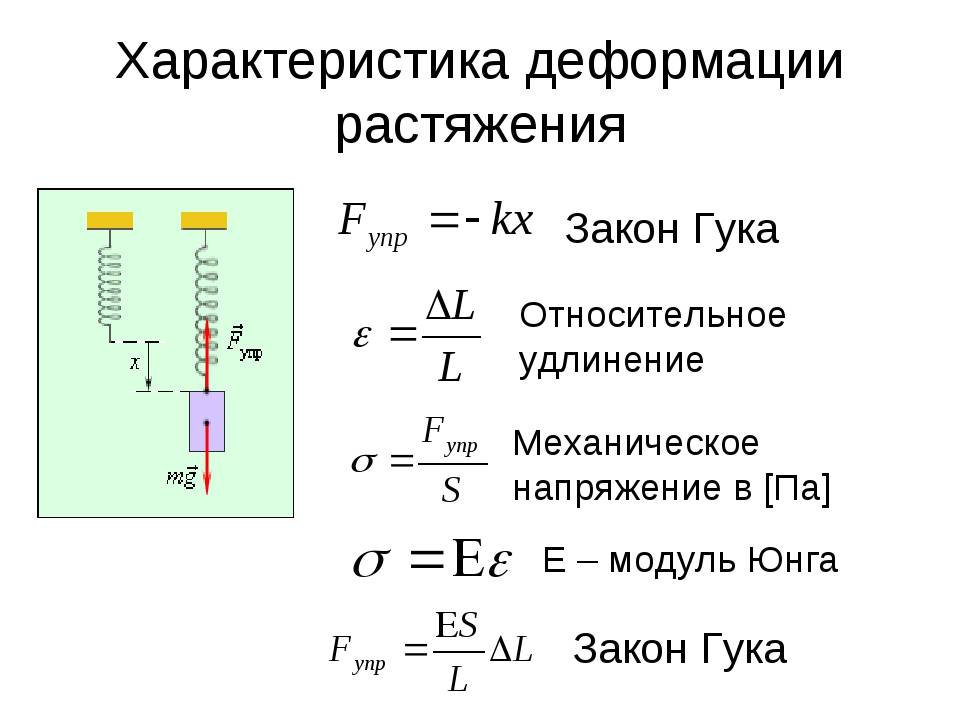
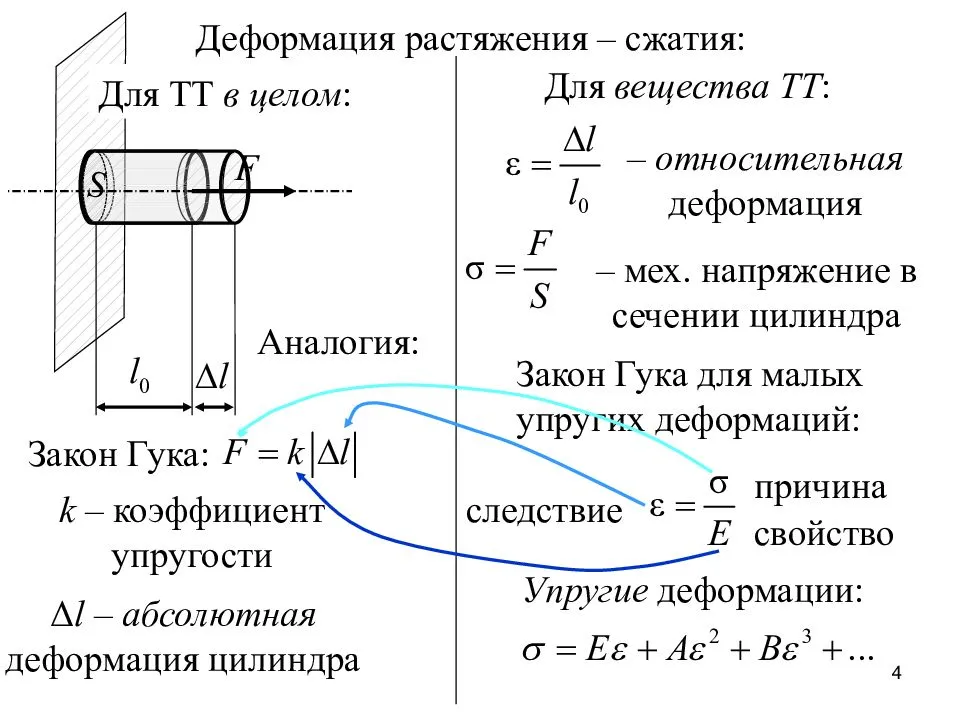
Для определения величины деформации пружины при растяжении можно применить закон Гука для пружин:
F=kx
В данном случае х – увеличение длины пружины, k – коэффициент жесткости (единица измерения Н/м), F – сила упругости, направленная в противоположную от смещения сторону. Величина абсолютной деформации будет равна отношению силы упругости к коэффициенту жесткости. Коэффициент жесткости определяет упругие свойства материала, используемого для изготовления, может быть использован для выбора материала изготовления в условиях решения конкретной задачи.
Что такое растяжение-сжатие
Прежде всего нужно сказать, что растяжение-сжатие — это такой вид деформации (относительного изменения размеров), при котором одно плоское сечение относительно другого удаляется параллельно исходному положению.
Пример деформации растяжения-сжатия. Схема приложения
Все это звучит сложно, но посмотрите видео и Вы все поймете!
Метод сечений в решении задач на растяжение-сжатие
Внутренние усилия при растяжении и сжатии. Растяжение-сжатие сопромат.
Load more
В первом видео уроке объясняется сам процес возникновения деформации растяжения-сжатия. Как отличить растяжение от сжатия. Приводится объяснение основного метода расчета задач по сопротивлению материалов — метод сечений.
Здесь рассмотрены задачи для стержня, имеющего сплошное поперечное сечение. На такой стержень может действовать как одна сила, так и несколько.
Растяжение-сжатие в стержневых конструкциях
Сопротивление материалов: Растяжение-сжатие в стержневых конструкциях, способ определения, Сопромат.
Load more
Во втором видео уроке приводится решение задачи на растяжение-сжатие для системы стержневых конструкций. Приведены методика и план решения задачи по сопротивлению материалов на тему растяжение-сжатие.
Так же из этого видеоурока станет что такое сумма моментов и как брать сумму моментов для того, чтобы найти нужное усилие или реакцию. Я это делаю по своей методике и обычно мои студенты довольны после объяснения.
Учет собственного веса в задачах на растяжение-сжатие
Растяжение и сжатие с учетом собственного веса. Сопротивление материалов.
Load more
Третья задача на растяжение-сжатие стержней с учетом собственного веса. Приведен пример решения задачи и доступно рассказывается как нужно учитывать собственный вес конструкции при расчете на растяжение-сжатие.
Растяжение-сжатие с учетом собственного веса в стержнях с двумя участками
Эпюра продольных сил. Как построить эпюру продольных сил при растяжении-сжатии
Load more
Задача на растяжение сжатие, более сложный случай. В этой задаче стержень состоит из нескольких участков. Здесь необходимо учитывать собственный вес — для стержня, испытывающего деформацию растяжения или сжатия, который состоит из нескольких участков. Здесь же приводится методика построения эпюр внутренних усилий при этих видах деформации.
Удлинение стержня при деформации растяжения-сжатия
Удлинение стержня при растяжении сжатии. Расчет стержня на жесткость
Load more
Приведен пример расчета на растяжение-сжатие когда нужно определить удлинение стержня. Удлинение (при растяжении) или укорочение (при сжатии) — это изменение размеров стержня вдоль оси приложения продольной нагрузки. Об этом в пятом видео уроке.
Определение удлинения стержня с учетом собственного веса при растяжении-сжатии
Учет собственного веса при определении удлинения стержня с двумя участками. Сопромат.
Load more
Определение изменения длины стержня с учетом собственного веса. Особенности формулы для определения удлинения (изменения длины) при растяжении-сжатии с учетом собственного веса.
Итак на этой странице приведены видеоуроки на основные темы в растяжении-сжатии. Планируется запись еще темы в которой будут рассматриваться статически неопределимые задачи на растяжение-сжатие.
Конечно это не все задачи, которые может понадобиться решить реальному инженеру, как инженеру-механику, так и инженеру-строителю. Встречаются разные случаи, когда нужно применять сообразительность.
Деформация изгиба
Рассмотрим примеры деформации данного вида. В случае изгиба, выпуклая часть тела подвергается некоторому растяжению, а вогнутый фрагмент сжимается. Внутри тела, подвергающегося данному варианту деформации, есть слой, который не испытывает ни сжатия, ни растяжения. Его принято называть нейтральным участком деформируемого тела. Вблизи него можно уменьшить площадь тела.
В технике примеры деформации данного типа используют для экономии материалов, а также для уменьшения веса возводимых конструкций. Сплошные брусья и стержни заменяют трубами, рельсами, двутавровыми балками.
для углеродистых и низколегированных сталей
Ст3, 09Г2С, 16ГС, 20, 20К, 10, 10Г2, 09Г2, 17ГС, 17Г1С, 10Г2С1:
- При расчетных температурах ниже 20°С допускаемые напряжения принимают такими же, как и при 20°С, при условии допустимого применения материала при данной температуре.
- Для промежуточных расчетных температур стенки допускаемое напряжение определяют линейной интерполяцией с округлением результатов до 0,5 МПа в сторону меньшего значения.
- Для стали марки 20 при Re/20e/20 / 220.
- Для стали марки 10Г2 при Rр0,2/20р0,2/20 / 270.
- Для стали марок 09Г2С, 16ГС классов прочности 265 и 296 по ГОСТ 19281 допускаемые напряжения независимо от толщины листа определяют для толщины свыше 32 мм.
- Допускаемые напряжения, расположенные ниже горизонтальной черты, действительны при ресурсе не более 105 ч. Для расчетного срока эксплуатации до 2*105 ч допускаемое напряжение, расположенное ниже горизонтальной черты, умножают на коэффициент: для углеродистой стали на 0,8; для марганцовистой стали на 0,85 при температуре < 450 °С и на 0,8 при температуре от 450 °С до 500 °С включительно.