Деформация кручения: напряжение, определение, примеры, формула,

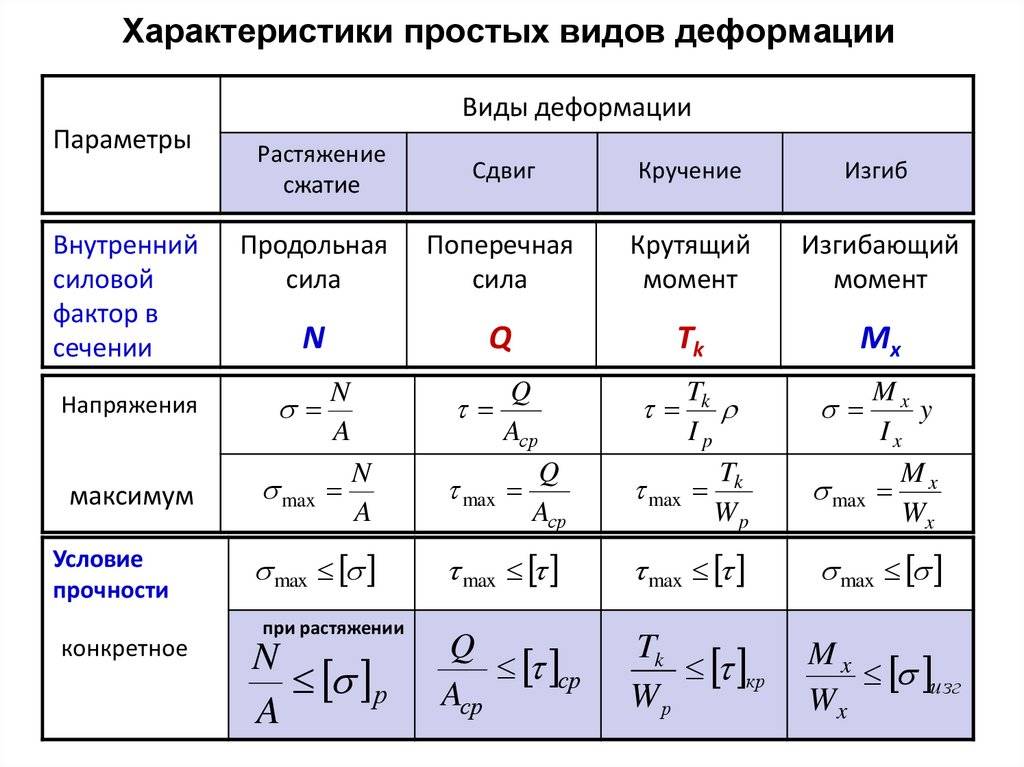
Измерение деформации

При проектировании и эксплуатации различных механизмов, технических объектов, зданий, мостов и других инженерных сооружений очень важно знать величину деформации материалов. Так как упругие деформации имеют маленькую величину, то измерения должны проводиться с очень высокой точностью

Для этого используют приборы, называемые тензометрами

Так как упругие деформации имеют маленькую величину, то измерения должны проводиться с очень высокой точностью. Для этого используют приборы, называемые тензометрами.

Тензометр состоит из тензометрического датчика и индикаторов. В него также может быть включено регистрирующее устройство.

В зависимости от принципа действия тензометры бывают оптические, пневматические, акустические, электрические и рентгеновские.

В основу оптических тензометров положено измерение деформации нити из оптоволокна, приклеенной к объекту исследования. Пневматические тензометры фиксируют изменение давления при деформации. В акустических тензометрах с помощью пьезоэлектрических датчиков проводятся измерения величин, на которые изменяются скорость звука и акустическое затухание при деформации. Электрические тензометры вычисляют деформацию на основе изменений электрического сопротивления. Рентгеновские определяют изменение межатомных расстояний в кристаллической решётке исследуемых металлов.

Вплоть до 80-х годов ХХ века сигналы датчиков регистрировались самописцами на обыкновенной бумажной ленте. Но когда появились компьютеры и начали бурно развиваться современные технологии, стало возможным наблюдать деформации на экранах мониторов и даже подавать управляющие сигналы, позволяющие изменить режим работы тестируемых объектов.

Деформация изгиба

Рассмотрим примеры деформации данного вида. В случае изгиба, выпуклая часть тела подвергается некоторому растяжению, а вогнутый фрагмент сжимается. Внутри тела, подвергающегося данному варианту деформации, есть слой, который не испытывает ни сжатия, ни растяжения. Его принято называть нейтральным участком деформируемого тела. Вблизи него можно уменьшить площадь тела.

В технике примеры деформации данного типа используют для экономии материалов, а также для уменьшения веса возводимых конструкций. Сплошные брусья и стержни заменяют трубами, рельсами, двутавровыми балками.

Сжатие и растяжение

Деформация растяжения связана с относительным либо абсолютным удлинением тела. В качестве примера можно привести однородный стержень, который закреплен с одного конца. При приложении вдоль оси силы, действующей в противоположном направлении, наблюдается растягивание стержня.

Сила же, прикладываемая по направлению к закрепленному концу стержня, приводит к сжатию тела. В процессе сжатия либо растяжения происходит изменение площади сечения тела.

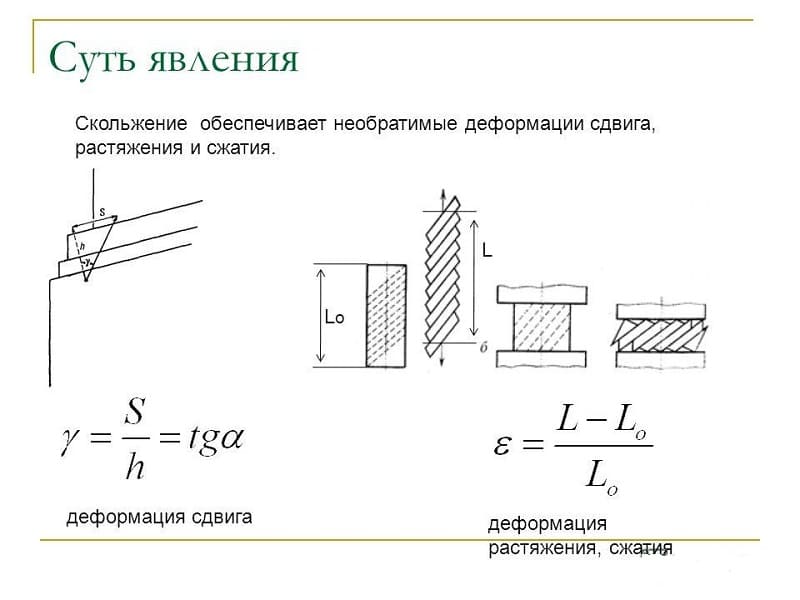
Деформация растяжения – это изменения состояния объекта, сопровождающиеся смещением его слоев. Данный вид можно проанализировать на модели твердого тела, состоящего из параллельных пластин, которые между собой соединены пружинками. За счет горизонтальной силы осуществляется сдвиг пластин на какой-то угол, объем тела при этом не меняется. В случае упругих деформаций между силой, приложенной к телу, и углом сдвига выявлена прямо пропорциональная зависимость.

Основные понятия

Под изгибом детали понимают естественное или искусственное изменение формы. Этот процесс разделяется на две категории – плоский или косой. В первом случае ось детали сохраняет своё первоначальное положение, во втором происходит её изменение в горизонтальной или вертикальной плоскости.

Основным теоретическим положением, определяющим физические процессы, протекающие в результате изгиба, является закон Гука. Согласно ему величина деформации (изгиба), пропорциональна приложенной к этому телу силе. Для каждого из видов деформации разработан индивидуальный расчёт действующих характеристик.

Оценка степени влияния действующих факторов на деформацию осуществляется с помощью следующих показателей:

площади поверхности подверженной деформации;
длины детали;
силы, воздействующие на конструкцию;
модуль упругости (его абсолютный показатель);
величина и характер изменения модуля длины в результате упругой деформации.

Одним из важных параметров считается потенциальная энергия деформации при изгибе. На основании этих параметров производят определение модуля Юнга. С его помощью рассчитывают скорость распространения продольной волны. Величина механического напряжения, при которой деформация тела всё ещё будет упругой, а сам объект способен восстановить первоначальную форму после снятия нагрузки, называется пределом упругости. При превышении допустимого значения этого параметра тело начнёт разрушаться. Этот предел называется прочностью. При оценке прочностных показателей применяют следующие предположения:

О постоянстве нормальных напряжений. Она определяет постоянство расстояний при возникновении напряжений изгиба.
Плоскости сечений. Оно называется гипотезой Бернулли. Сечения детали в спокойном положении находятся в плоском состоянии. После деформации они сохраняют первоначальную форму, но разворачиваются относительно некоторой линии. Она называется нейтральной осью.
Отсутствие давлений на боковые поверхности. Считается, что соседние волокна не оказывают давления друг на друга.

Перечисленные гипотезы позволяют оценить деформации сдвига и характер изгиба каждого слоя исследуемой детали. Это происходит в результате воздействия различных сил. Нагрузки вызывают деформацию изгиба в различных плоскостях. Они подразделяются на две категории:

характеру воздействия (статические или динамические);
степени воздействия (массовые или объёмные);
поверхности (сосредоточенные, воздействуют на отдельные элементы поверхности и распределёнными – на всю поверхность).

К статическим относятся нагрузки, у которых место приложения и направления сил не меняется или изменяются медленно в течение определённого промежутка времени. К таким нагрузкам относится сила тяжести. В этом случае можно принять утверждение, что элементы физического объекта находятся в состоянии равновесия. У динамических нагрузок эти параметры меняются достаточно быстро или носят импульсивный характер. К ним относятся ударные нагрузки при забивании свай, обработке металла ковкой, воздействие неровностей дороги на колесо.

При сосредоточенной статической нагрузке на отдельный участок поверхности бруса происходит его деформация в сторону по направлению сил взаимодействия. Для расчёта параметров характеризующих основные показатели состояния деформированного тела применяют дифференциальные уравнения, которые позволяют выявить существующие функциональные связи. По деформации изгиба с помощью модуля Юнга можно вычислить прочность исследуемого элемента конструкции (балки, бруса, подвесной опоры и т. д.). На основании полученных областей решения можно построить графическое изображение силы упругости, которое наглядно показывает, что происходит с различными участками деформированной детали. Для каждой детали в зависимости от её геометрических размеров, материала изготовления и величины приложенных сил выведена своя формула.

Для наглядности восприятия характера протекающих процессов использует метод нанесения эпюр на поверхность объекта. Эта операция называется топология. Основной идеей является проецирование линий нагрузки на соответствующую плоскость (горизонтальную, фронтальную или профильную). В современных методах топологии применяют фрактальную геометрию.

Кручение

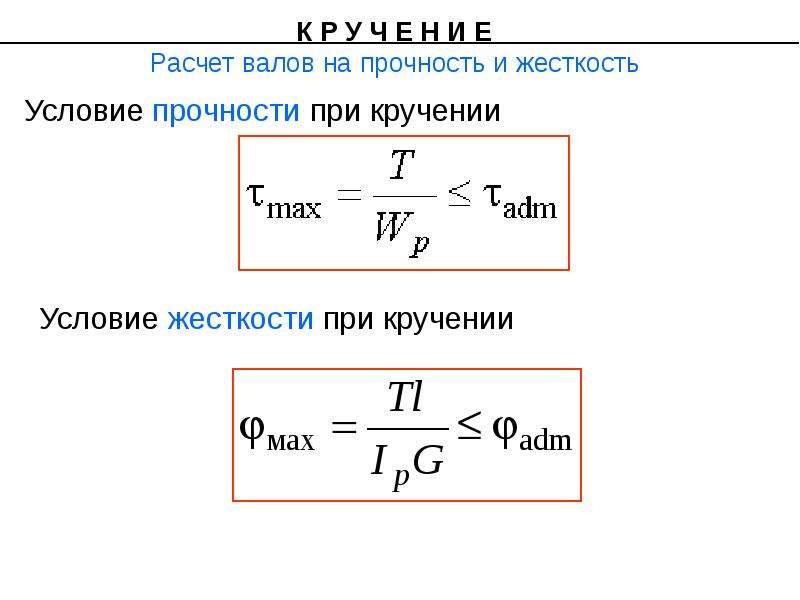
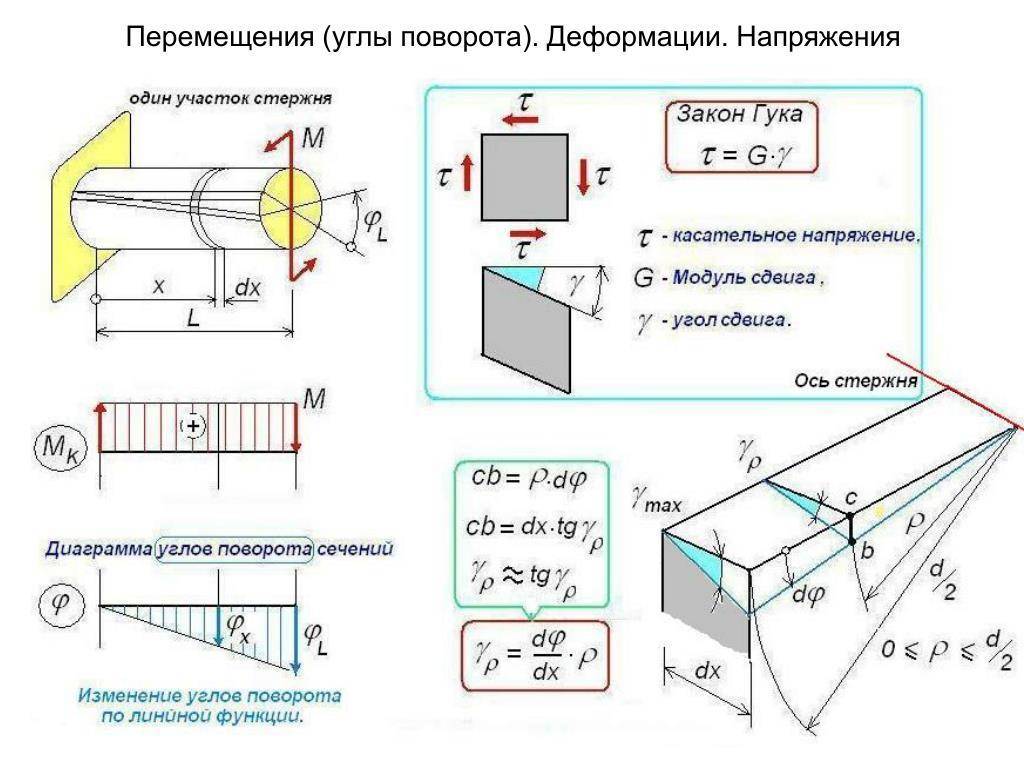
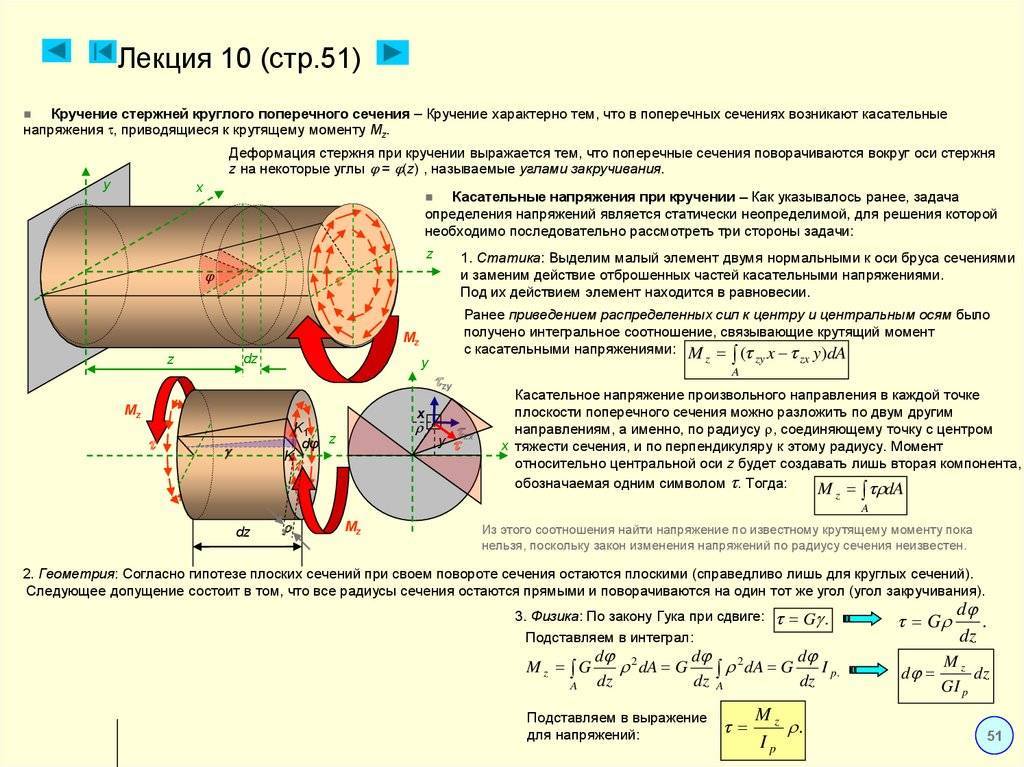
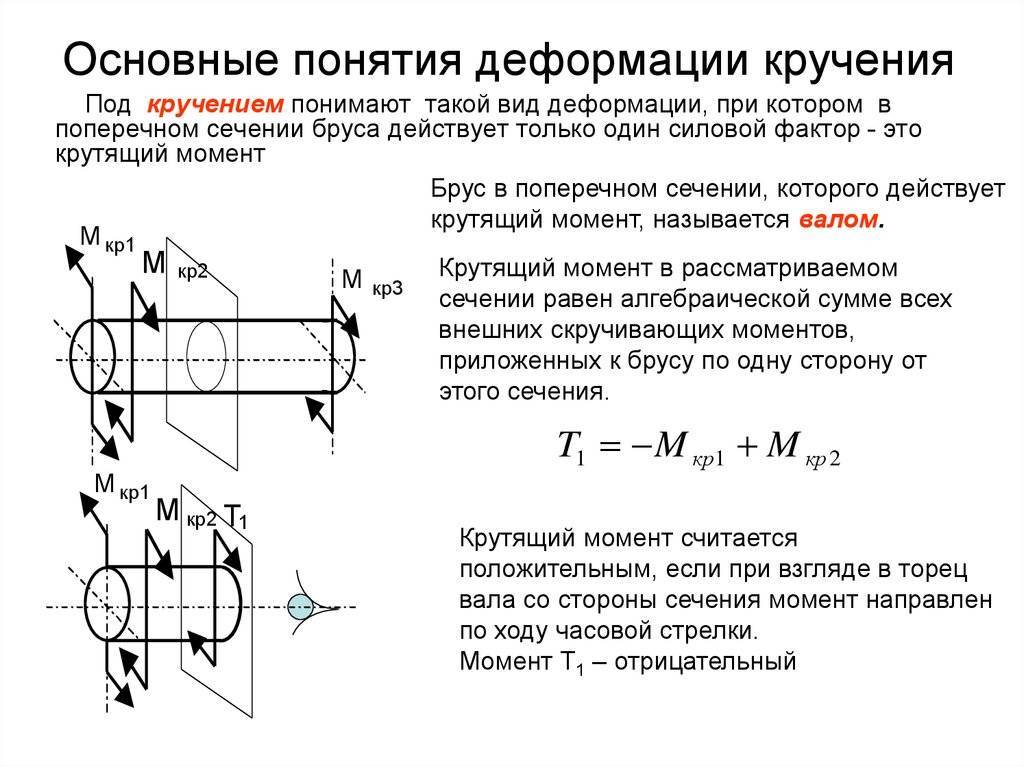
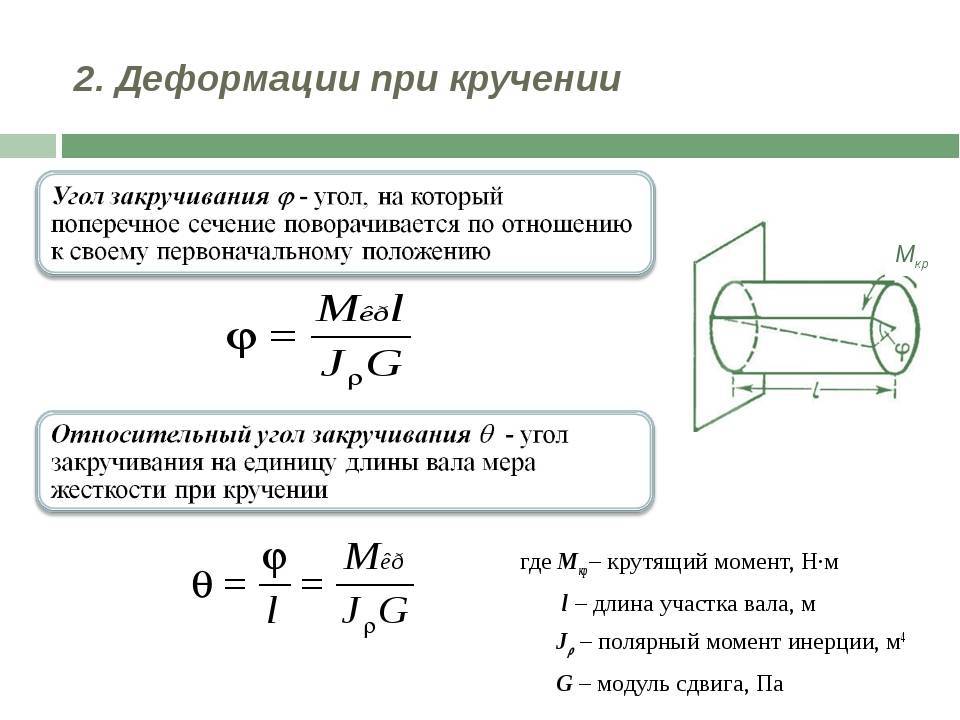
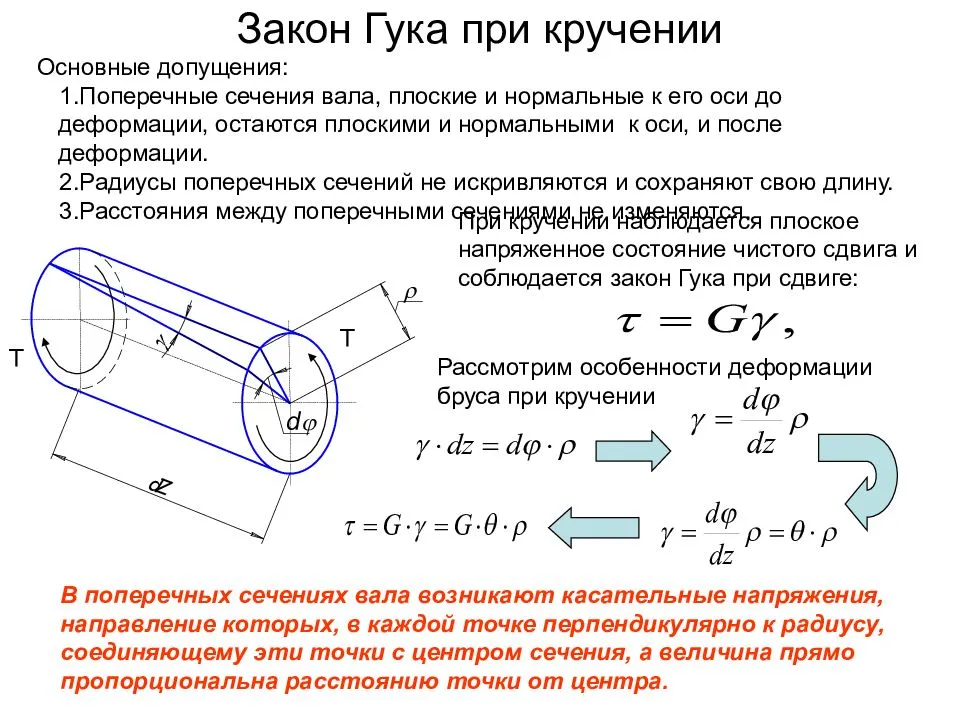
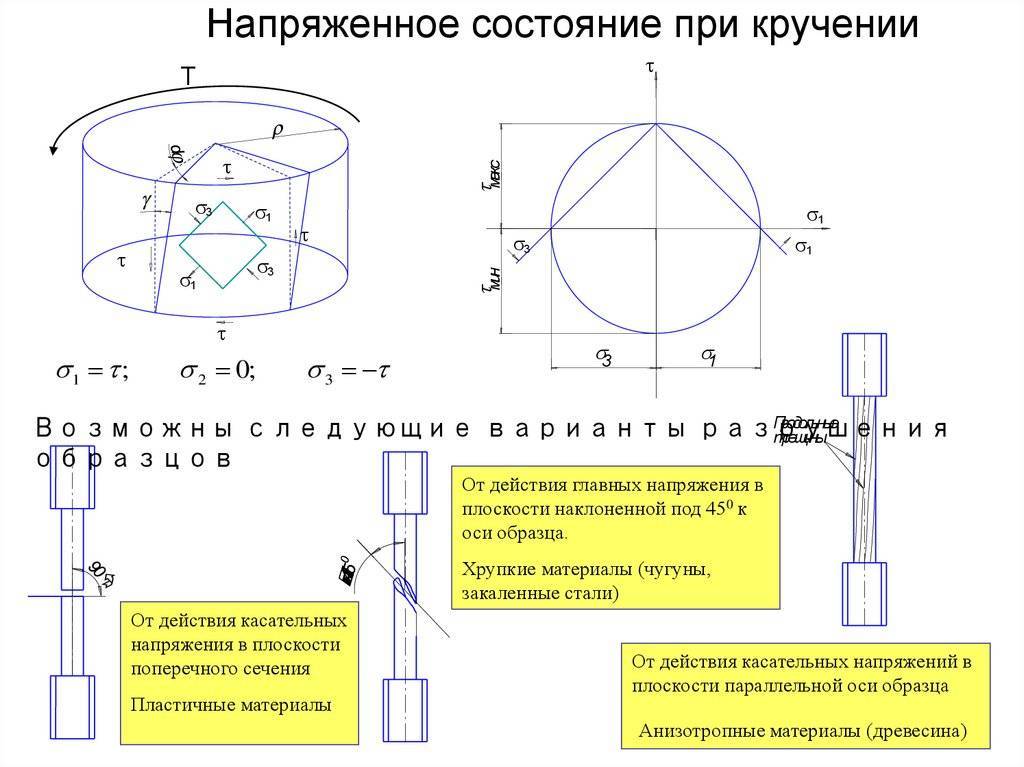
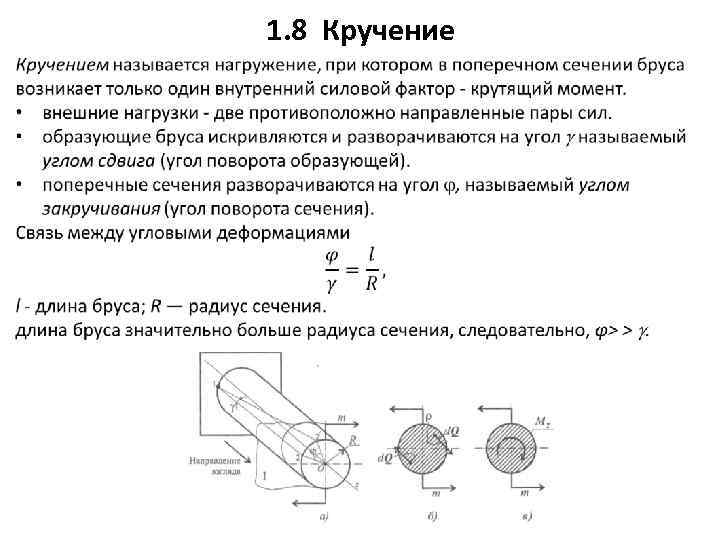
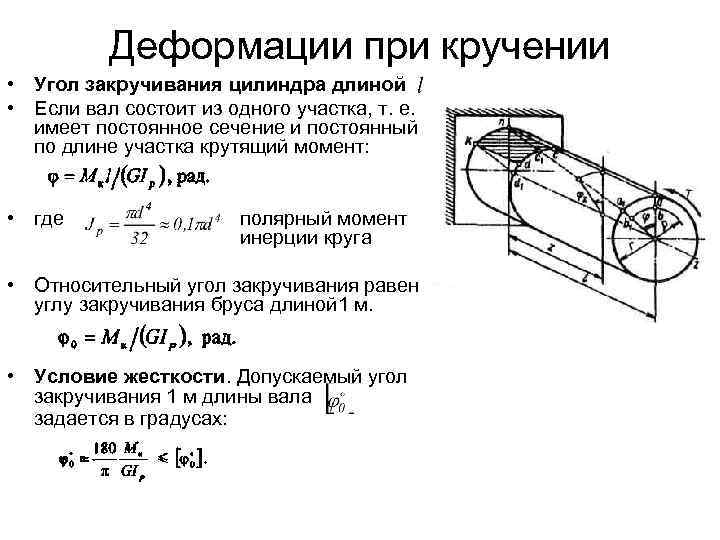
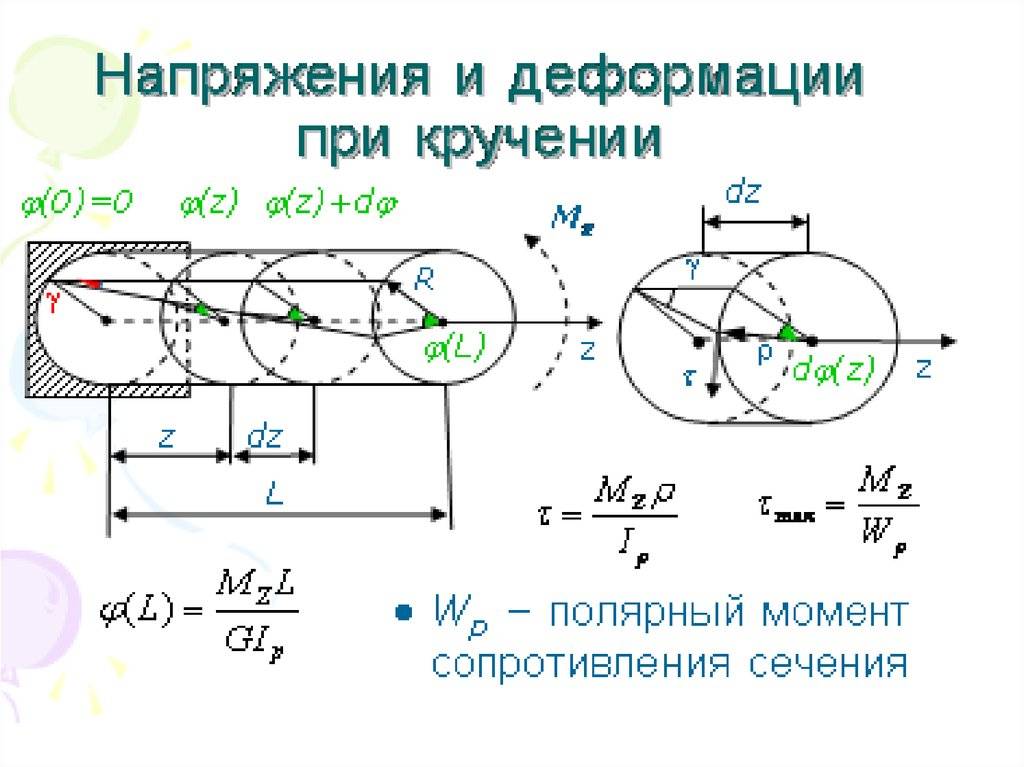
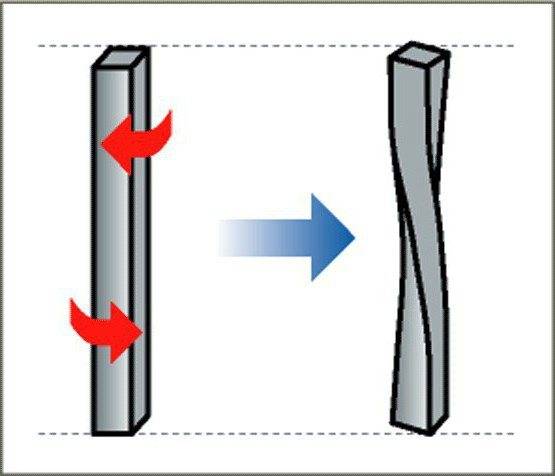
Кручение — один из видов деформации тела. Возникает в том случае, если нагрузка прикладывается к телу в виде пары сил (момента) в его поперечной плоскости. При этом в поперечных сечениях тела возникает только один внутренний силовой фактор — крутящий момент. На кручение работают пружины растяжения-сжатия и валы. При деформации кручения смещение каждой точки тела перпендикулярно к её расстоянию от оси приложенных сил и пропорционально этому расстоянию.

Деформацию кручения можно наблюдать, если на стержень, один конец которого закреплен, действует пара сил, лежащих в плоскости, перпендикулярной оси стержня. При кручении отдельные слои тела остаются параллельными, но поворачиваются друг относительно друга на некоторый угол. Деформация кручения представляет собой неравномерный сдвиг. Деформации кручения возникают при завинчивании гаек, при работе валов машин.

Пример деформации кручения цилиндрического стержня

Если проволоку или стержень, закрепленные с одного конца, закручивать, прилагая к другому концу пару сил F с моментом, равным М, то стержень (проволока) претерпевает деформацию кручения, при которой одно его основание поворачивается по отношению к другому, фиксированному, на некоторый угол φ – угол кручения (рис. 1; 2).

Рис. 1.

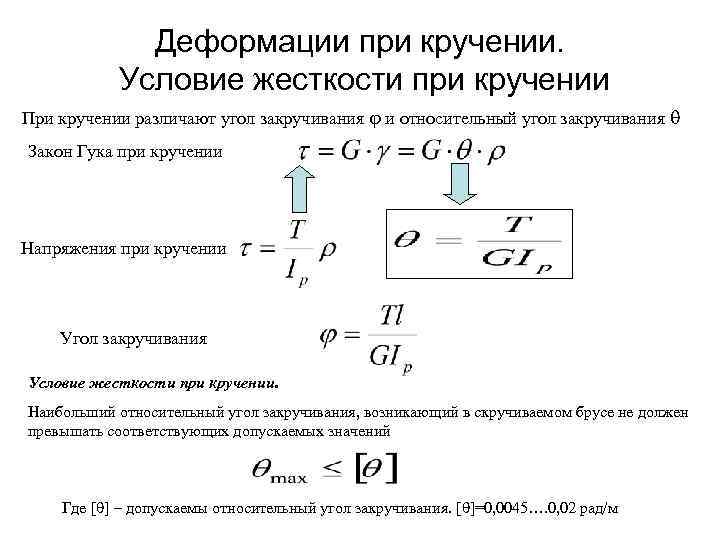
Отношение угла закручивания φ к длине называют относительным углом закручивания

Закон Гука для малых деформаций кручения выражается формулой

M = Gкр.j

где Gкр.– модуль кручения.

Модуль кручения , помимо материала, зависит также от формы и размеров тела.

Представьте, перед вами цилиндр (или проволока). Если вы начнёте его (её) верхний конец поворачивать вдоль оси, закрепив нижний конец, то при повороте верхней грани на один радиан вы прикладываете вращающий момент, в точности равный модулю кручения (рис.1; 2). Это и есть его определение.

Модуль кручения Gкр показывает, какой момент силы нужно приложить, чтобы закрутить проволоку на угол в 1 рад.

Рис. 2.

Деформация кручения является частным случаем деформации сдвига.

Сдвиг

Сдвигом называют такую деформацию твердого тела, при которой все его плоские слои, параллельные некоторой плоскости сдвига, не искривляясь и не изменяясь в размерах, смещаются параллельно друг другу (рис. 3).

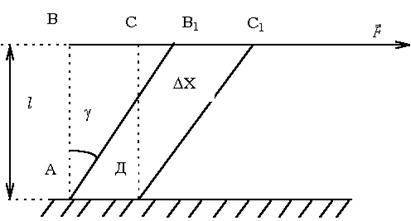
Рис. 3.

Деформация сдвига возникает под действием сил, приложенных к двум противоположным граням тела так, как показано на рисунках 3; 4. Эти силы вызывают смещение слоев тела, параллельных направлению сил. Расстояние между слоями не изменяется. Любой прямоугольный параллелепипед, мысленно выделенный в теле, превращается в наклонный.

Рис. 4.

Мерой деформации сдвига является угол сдвига γ — угол наклона вертикальных граней (рис. 5).

Рис. 5.

Сдвиг происходит под действием касательной силы F, приложенной к грани ВС, параллельной плоскости сдвига. Грань АД, параллельная ВС, закреплена неподвижно.

Так как угол мал, формулу можно записать в виде:

где СС1 = D X — абсолютный сдвиг, γ — угол сдвига, называемый также относительным сдвигом, выражается в радианах.

По закону Гука относительный сдвиг γ пропорционален касательному напряжению τ = F/S, где S — площадь поверхности грани ВС, т.е.

τ = F / S = Gg

где G — модуль сдвига.

Закон Гука для малой деформации сдвига выражается формулой:

Коэффициент G, зависящий от материала тела, называется модулем сдвига и характеризует упругие свойства тела при деформации сдвига. Например, для стального образца G = 76 ГПа.

Модуль сдвига равен касательному напряжению, которое возникло бы в образце при относительном сдвиге, равном 1 (при условии, что закон Гука выполняется).

Деформацию сдвига испытывают, например, заклепки и болты, соединяющие металлические конструкции. Сдвиг при больших углах приводит к разрушению тела — срезу. Срез происходит при работе ножниц, пилы и др.

Обратите внимание на принципиальное отличие модуля кручения от модуля сдвига, который зависит только от материала. Модуль кручения зависит не только от материала, но ещё и от диаметра и от длины цилиндра

Определение и общие сведения о деформации сдвига

Основным признаком, характеризующим деформацию сдвига, является сохранение постоянства объёма. Не зависимо от того, в каком направлении действуют силовые факторы этот параметр остаётся неизменным.

Примеры проявления деформации сдвига можно обнаружить при проведении различного рода работ. К таким случаям относятся:

при распиловке бруса;
отрезание или рубка металла;
в результате нарушения целостности крепления металлических или деревянных деталей, соединённых метизами;
балки в местах крепления опор;
места скрепления мостовых пролётов;
крепёж на перемычках соединения железнодорожных рельс;
разрезания листа бумаги ножницами.

При определённых условиях наблюдается чистый сдвиг. Он определяется как сдвиг, при котором на все четыре грани (например, прямоугольной детали) оказывают воздействие только напряжения, направленные по касательной к поверхности. В этом случае произойдёт плавный сдвиг всех слоёв детали от верхних к нижним слоям. Тогда внешняя сила изменяет форму детали, а объём сохраняется.

Для оценки величины сдвига и надёжности конструкции используют следующие параметры:

величина, направление и точка приложения воздействующей силы;
модуль сдвига;
угол изменения внешних граней изделия;
тангенциальное напряжение;
модуль кручения (зависит от физико-механических характеристик материала);

Расчёт и практическое измерение этих параметров необходимы для оценки устойчивости и целостности конструкции. Формула, позволяющая вычислить допустимые изменения, учитывает все воздействия на конкретные слои детали и всю конструкции в целом.

В случае воздействия деформации величина угла считается пропорциональной внешней силе. Увеличение степени воздействия может превратить деформацию сдвига в срез. Это приведёт к разрушению не только элементов крепления (болтов, шпилек, заклёпок), но и всей детали.

Для наглядности изменения формы детали при деформации сдвига динамика процесса обозначается с помощью величины угла смещения и векторов возникающих напряжений. Действующая сила направлена в сторону смещения слоёв рассматриваемой детали.

В современных условиях угол сдвига измеряется различными техническими приборами. Основным прибором для измерения параметров смещения является тензомер. Эти приборы работают на различных физических принципах:

оптические (в том числе лазерные);
акустические;
рентгеновские; электрические;
пневматические.

В этих приборах относительная деформация сдвига обрабатывается на современных вычислительных средствах с применением соответствующего программного обеспечения. Каждый метод обладает своими достоинствами и недостатками. Их применение зависит от поставленной задачи, технической и финансовой возможности.

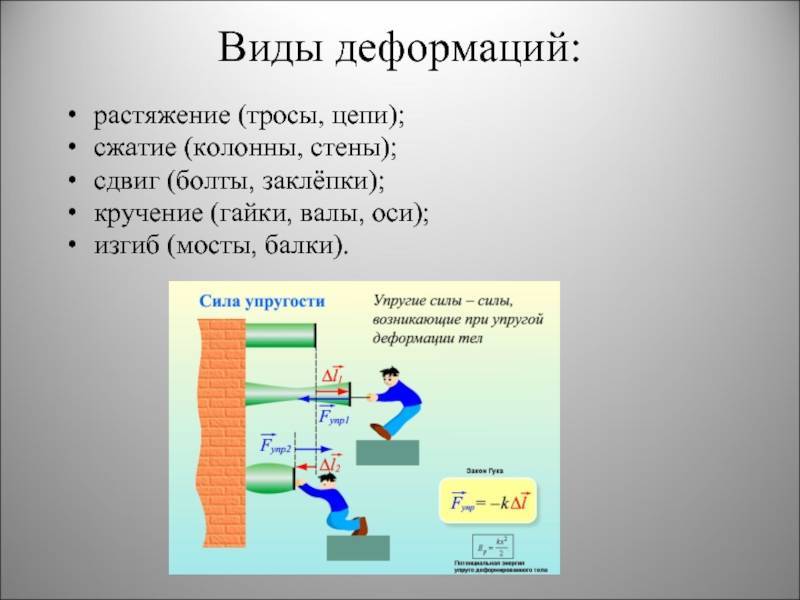
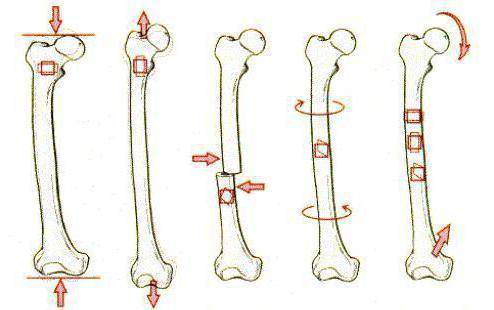
Виды деформации твердых тел

Деформация растяжения

Деформация растяжения — вид деформации, при которой нагрузка прикладывается продольно от тела, то есть соосно или параллельно точкам крепления тела. Проще всего растяжение рассмотреть на буксировочном тросе для автомобилей. Трос имеет две точки крепления к буксиру и буксируемому объекту, по мере начала движения трос выпрямляется и начинает тянуть буксируемый объект. В натянутом состоянии трос подвергается деформации растяжения, если нагрузка меньше предельных значений, которые может он выдержать, то после снятия нагрузки трос восстановит свою форму.

Схема растяжения образца

Посмотрите прибор измеряющий деформацию растяжения →

Деформация растяжения является одним из основных лабораторных исследований физических свойств материалов. В ходе приложения растягивающих напряжений определяются величины, при которых материал способен:

воспринимать нагрузки с дальнейшим восстановлением первоначального состояния (упругая деформация)
воспринимать нагрузки без восстановления первоначального состояния (пластическая деформация)
разрушаться на пределе прочности

Данные испытания являются главными для всех тросов и веревок, которые используются для строповки, крепления грузов, альпинизма. Растяжение имеет значение также при строительстве сложных подвесных систем со свободными рабочими элементами.

Деформация сжатия

Деформация сжатия — вид деформации, аналогичный растяжению, с одним отличием в способе приложения нагрузки, ее прикладывают соосно, но по направлению к телу. Сдавливание объекта с двух сторон приводит к уменьшению его длины и одновременному упрочнению, приложение больших нагрузок образовывает в теле материала утолщения типа «бочка».

Схема сжатия образца

В качестве примера можно привести тот же прибор что и в деформации растяжения немного выше.

Деформация сжатия широко используется в металлургических процессах ковки металла, в ходе процесса металл получает повышенную прочность и заваривает дефекты структуры

Сжатие также важно при строительстве зданий, все элементы конструкции фундамента, свай и стен испытывают давящие нагрузки. Правильный расчет несущих конструкций здания позволяет сократить расход материалов без потери прочности

Деформация сдвига

Деформация сдвига — вид деформации, при котором нагрузка прикладывается параллельно основанию тела. В ходе деформации сдвига одна плоскость тела смещается в пространстве относительно другой. На предельные нагрузки сдвига испытываются все крепежные элементы — болты, шурупы, гвозди. Простейший пример деформации сдвига – расшатанный стул, где за основание можно принять пол, а за плоскость приложения нагрузки – сидение.

Схема сдвига образца

Посмотрите прибор измеряющий деформацию сдвига →

Деформация изгиба

Деформация изгиба — вид деформации, при котором нарушается прямолинейность главной оси тела. Деформации изгиба испытывают все тела подвешенные на одной или нескольких опорах. Каждый материал способен воспринимать определенный уровень нагрузки, твердые тела в большинстве случаев способны выдерживать не только свой вес, но и заданную нагрузку. В зависимости от способа приложения нагрузки при изгибе различают чистый и косой изгиб.

Схема изгиба образца

Посмотрите прибор измеряющий деформацию изгиба →

Значение деформации изгиба важно для проектирования упругих тел, таких, как мост с опорами, гимнастический брус, турник, ось автомобиля и другие

Деформация кручения

Деформация кручения – вид деформации, при котором к телу приложен крутящий момент, вызванный парой сил, действующих в перпендикулярной плоскости оси тела. На кручение работают валы машин, шнеки буровых установок и пружины.

Схема кручения образца

Посмотрите прибор измеряющий деформацию кручения →

Материал волосков

Материал, из которого производят ресницы для наращивания, бывает нескольких видов.

Натуральный животный мех. Используются волоски из ушей или хвостов белок, лис, песцов, которые обрабатываются особым образом. Они мягкие, легкие и эластичные.

Из минусов материала мастера выделяют:

неодинаковые изгиб, длину и толщину;
постепенное выгорание цвета;
аллергические реакции у женщин с чувствительными глазами;
изменение изгиба во время носки под воздействием внешних факторов среды (влажность, температура).

В связи с большим количество отрицательных качеств, данный материал редко используется профессиональными мастерами.

Каучуковое природное волокно. Отличаются высокой эластичность, достаточной прочность. В редких случаях способны провоцировать аллергические реакции.

У ресниц один существенный минус – неоправданно высокая стоимость. Вследствие чего увеличивается стоимость всей процедуры, поэтому такие ресницы может позволить себе не каждая женщина.

Синтетическое волокно. Наиболее часто используемый вид материала.

Выделяют три основных вида моноволокон, из которых изготавливаются волоски:

1. Полированный акрил. Из него производились первые ресницы для наращивания. Они были достаточно жесткими и прочными, имели ярко выраженный глянцевый блеск. У них отсутствовала градация по диаметру и изгибу (в основном это был С, D-изгиб толщиной 0,24 мм). В носке доставляли дискомфорт из-за низкой эластичности.

2. Полиэстер. К достоинствам материала мастера относят

эластичность и мягкость в работе и последующей ежедневной носке;
низкую степень деформированности;
однородность цвета по всей длине;
гипоаллергенность;
отсутствие возможности выгорания;
гидрофобность.

Материал по праву занимает лидирующее место на рынке производства искусственных ресниц.

3. Полибутилентерефталат (РВТ) – обладает аналогичными с полиэстером положительными характеристиками, удобен в работе. Отличием является большая вариабельность вариантов исполнения ресниц.

Выделяют:

матовое волокно (норка) – имеет глубокий черный цвет, подходит для естественного эффекта при наращивании;
глянцевое волокно (соболь, силикон) – более тяжелые, яркие волоски. С их помощью можно добиться эффекта подведенных глаз;
полуматовое волокно (шелк) – самые легкие из производимых ресниц. Подходят для наращивания на тонкие, ослабленные ресницы. Минусом является их цвет – он более светлый, с серым оттенком.

Измерение деформации

Для этого используют приборы, называемые тензометрами

Закон Гука

От чего же зависит сила упругости? Роберт Гук, современник Ньютона, ответил на этот вопрос (рисунок 8).

Рисунок 8. Английский физик и изобретатель Роберт Гук (1635-1703). Установил зависимость силы упругости от деформации тела.

Рассмотрим опыт, изображенный на рисунке 9.

Рисунок 9. Опыт на определение зависимости силы упругости от деформации тела.

У нас есть штатив, к которому мы прикрепим резиновый шнур. Измерим его длину и обозначим как $l_0$.

Далее подвесим к шнуру чашку с гирей. Шнур удлинится. Снова измерим его длину — теперь она имеет значение $l$.

Шнур изменил свою длину после наших действий. Это изменение (удлинение шнура) мы можем найти по формуле:

$$\Delta l = l- l_0$$

где $\Delta l$ — изменение длины. Знак $\Delta$ (греческая буква “дельта”) используется как символ для обозначения изменения между значениями какой-либо величина.

Если мы будем менять гири на чашке, то будет меняться длина шнура, т.е. его удлинение (деформация) $\Delta l$.

Этот опыт показывает, что

Так мы подошли к закону Гука:

$$F_{упр} = k \Delta l$$

Где $ \Delta l$ — изменение длины тела, $k$ — коэффициент пропорциональности, который называется жесткостью. Жесткость тела зависит от материала, формы и размеров тела.

{"questions":,"explanations":,"answer":}},"hints":[]}]}

Заключение

Деформации, рассматриваемые в курсе школьной физики, оказывают влияние на процессы, происходящие в живом мире. В организмах человека, животных постоянно происходит кручение, изгиб, растяжение, сжатие. И для того чтобы осуществлять своевременную и полноценную профилактику проблем, связанных с осанкой или избыточным весом, медики используют зависимости, выявленные физиками при проведении фундаментальных исследований.

Например, прежде чем осуществлять протезирование нижних конечностей, выполняется детальный расчет максимальной нагрузки, на которую он должен быть рассчитан

Протезы подбираются для каждого человека индивидуально, так как важно учесть вес, рост и подвижность последнего. При нарушениях осанки применяют специальные коррекционные пояса, основанные на использовании деформации сдвига

Современная реабилитационная медицина не смогла бы существовать без использования физических законов и явлений, в том числе и без учета закономерностей различных видов деформаций

Деформация кручения

Измерение деформации

Деформация изгиба

Сжатие и растяжение

Основные понятия