Кинетическая энергия пружины

Работа.

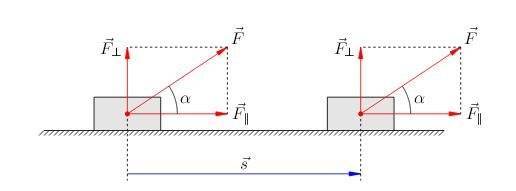
Пусть на тело действует постоянная сила и тело, двигаясь прямолинейно по горизонтальной поерхности, совершило перемещение . Сила не обязательно является непосредственной причиной перемещения (так, сила тяжести не является непосредственной причиной перемещения шкафа, который передвигают по комнате). Предположим сначала, что векторы силы и перемещения сонаправлены (рис. 1; остальные силы, действующие на тело, не указаны)

Рис. 1.A=Fs

В этом простейшем случае работа определяется как произведение модуля силы на модуль перемещения:

. (1)

Единицей измерения работы служит джоуль (Дж): Дж=Н м. Таким образом, если под действием силы 1 Н тело перемещается на 1 м, то сила совершает работу 1 Дж.

Работа силы, перпендикулярной перемещению, по определению считается равной нулю. Так, в данном случае сила тяжести и сила реакции опоры не совершают работы.

Пусть теперь вектор силы образует с вектором перемещения острый угол (рис. 2).

Рис. 2. A=Fs cos

Разложим силу на две составляющие: (параллельную перемещению) и (перпендикулярную перемещению). Работу совершает только . Поэтому для работы силы получаем:

. Итак,

. (2)

Если вектор силы образует с вектором перемещения тупой угол , то работа по-прежнему определяется формулой (2). В этом случае работа оказывается отрицательной.

Например, работа силы трения скольжения, действующей на тело в рассмотренных ситуациях, будет отрицательной, так как сила трения направлена противоположно перемещению. В этом случае имеем:

, и для работы силы трения получаем:

,

где — масса тела, — коэффициент трения между телом и опорой.

Соотношение (2) означает, что работа является скалярным произведением векторов силы и перемещения:

Это позволяет вычислять работу через координаты данных векторов:

Пусть на тело действуют несколько сил и — равнодействующая этих сил. Для работы силы имеем:

,

или

,

где — работы сил . Итак, работа равнодействующей приложенных к телу сил равна сумме работ каждой силы в отдельности.

Сила упругости и закон Гука

Для начала определим основные термины, которые будут использоваться в данной статье. Известно, если воздействовать на тело извне, оно либо приобретет ускорение, либо деформируется. Деформация — это изменение размеров или формы тела под влиянием внешних сил. Если объект полностью восстанавливается после прекращения нагрузки, то такая деформация считается упругой; если же тело остается в измененном состоянии (например, согнутом, растянутом, сжатым и т. д. ), то деформация пластическая.

Примерами пластических деформаций являются:

лепка из глины;
погнутая алюминиевая ложка.

В свою очередь, упругими деформациями будут считаться:

резинка (можно растянуть ее, после чего она вернется в исходное состояние);
пружина (после сжатия снова распрямляется).

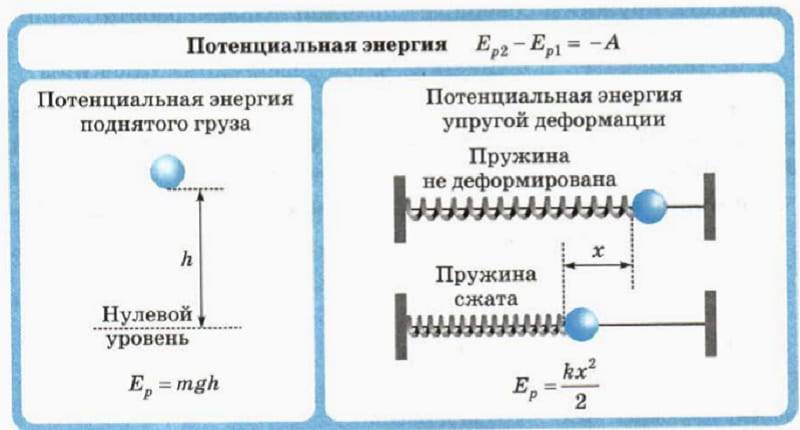
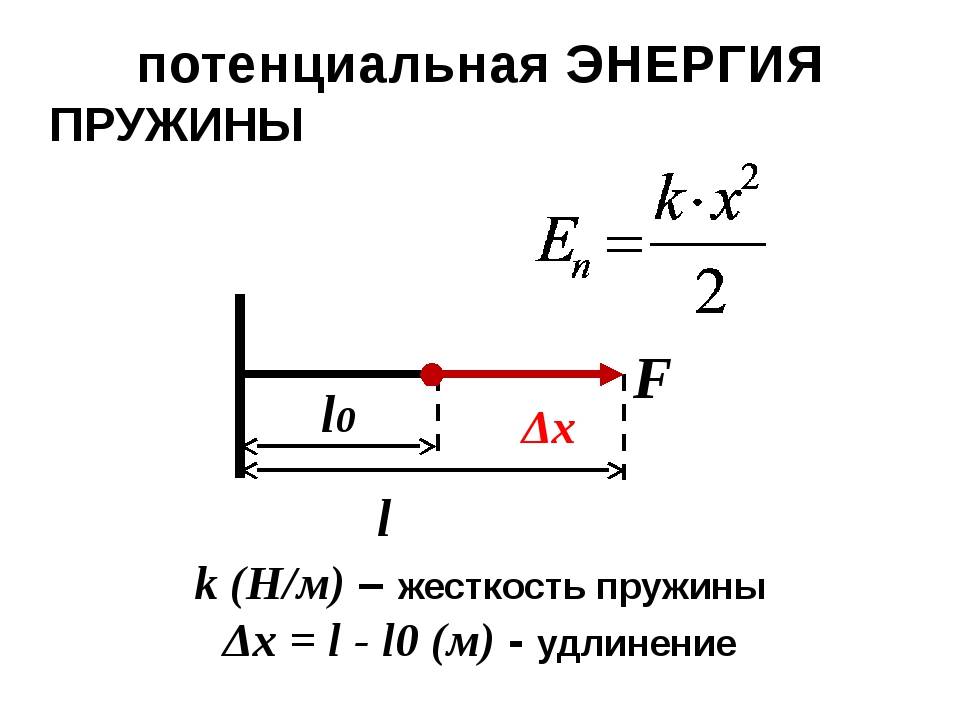
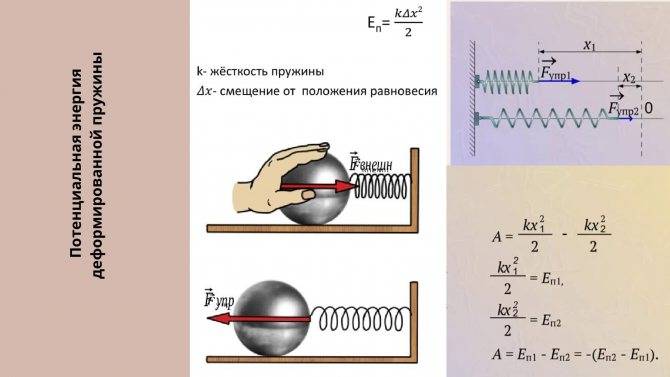
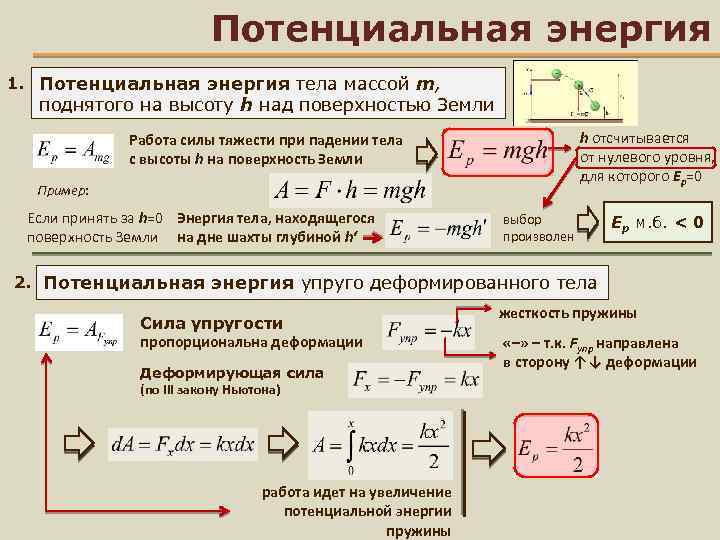
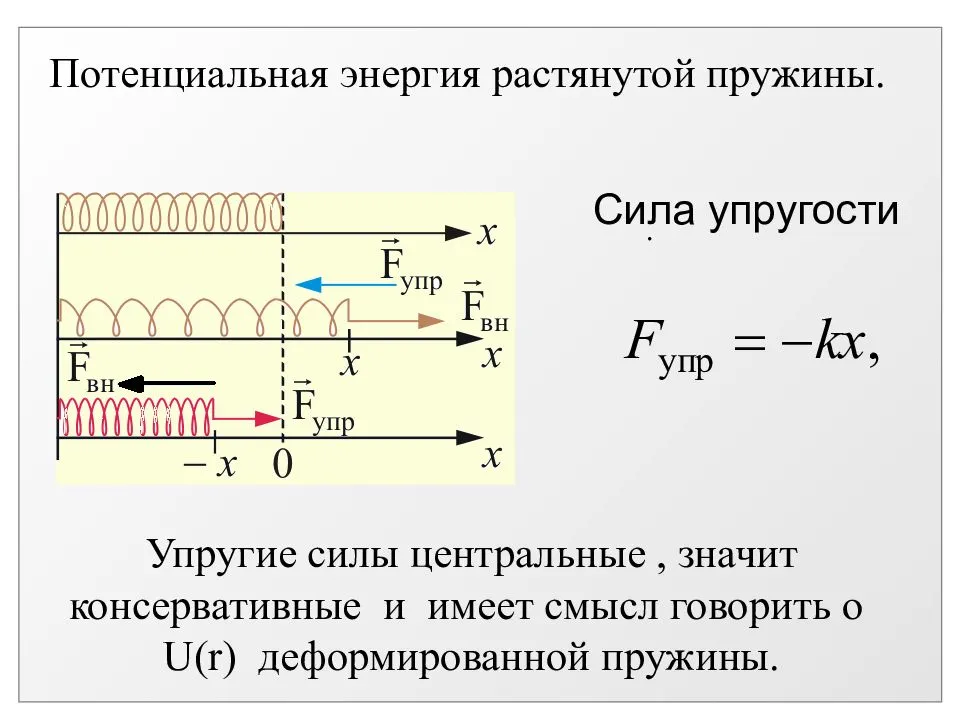
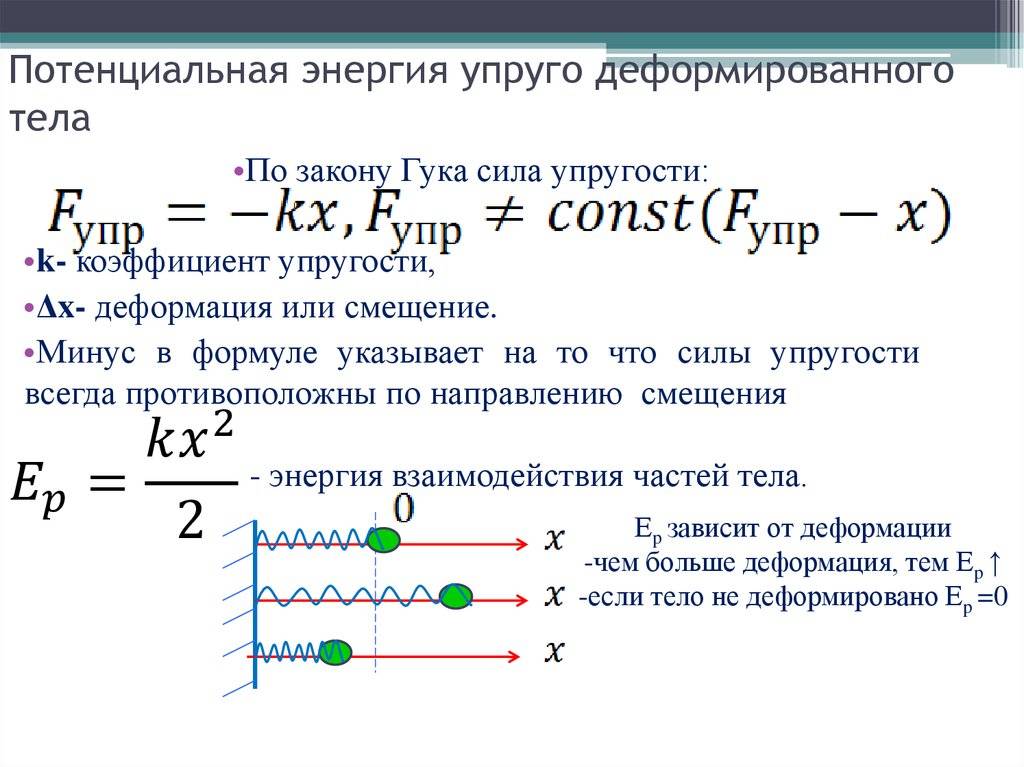
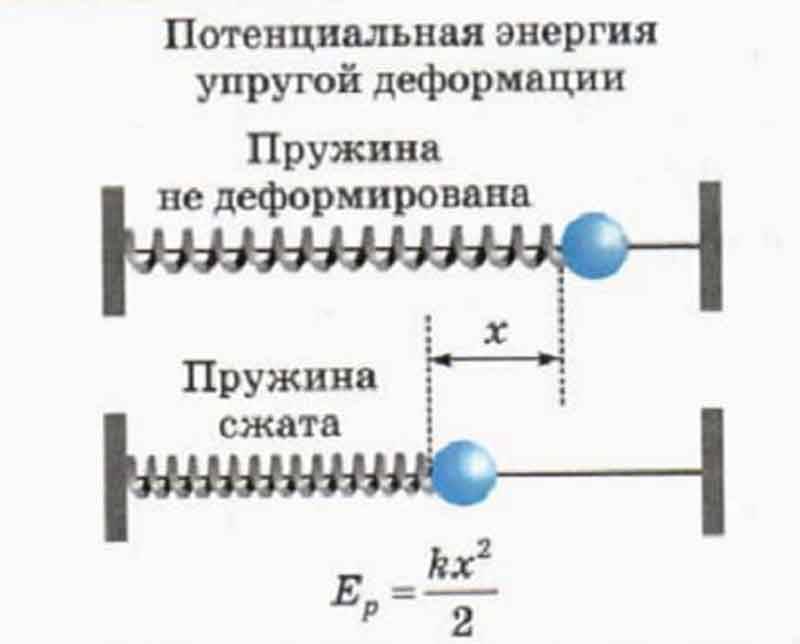
В результате упругой деформации тела (в частности, пружины) в нем возникает сила упругости, равная по модулю приложенной силе, но направленная в противоположную сторону. Сила упругости для пружины будет пропорциональна ее удлинению. Математически это можно записать таким образом:

F = — k·x;

где F — сила упругости, x — расстояние, на которое изменилась длина тела в результате растяжения, k — необходимый для нас коэффициент жесткости. Указанная выше формула также является частным случаем закона Гука для тонкого растяжимого стержня. В общей форме этот закон формулируется так: «Деформация, возникшая в упругом теле, будет пропорциональна силе, которая приложена к данному телу». Он справедлив только в тех случаях, когда речь идет о малых деформациях (растяжение или сжатие намного меньше длины исходного тела).

Средняя кинетическая энергия

В большинстве случаев проводится высчитывание среднего значения. Этот показатель не учитывает то, в каких положениях сила упругости высокая и низкая. Для расчета применяется формула: F=kl/2.

В данном случае достаточно знать лишь удлинение, которое измеряется при использовании обычного инструмента. Что касается коэффициента, то он может варьировать в достаточно большом диапазоне, зависит от следующих моментов:

Диаметра витков. С увеличением этого показателя существенно повышается коэффициент жесткости, изделие часто используется для выполнения большой работы.
Толщины применяемой проволоки. Рассматриваемое изделие представлено проволокой, которая накручивается вокруг установленной оси.
Расстояния между отдельными витками. Как правило, они расположены относительно друг друга на определенном расстоянии, которое одинаковое. По этому признаку выделяют варианты исполнения, предназначенные для сжатия и растяжения.
Типа применяемого материала при изготовлении. Некоторые сплавы характеризуются достаточно высокой жесткостью, могут переносить незначительную деформацию.

Коэффициент самостоятельно рассчитать не нужно, он берется с определенных таблиц. Среднее значение часто высчитывается в случае решения математических задач, при проектировании применяются другие формулы.

Что такое кинетическая энергия

Кинетическая энергия – это энергия, создаваемая движущимся телом. На греческом языке кинетика означает «движение», в то время как энергия означает «работа». Другими словами, кинетическая энергия – это работа, которую тело выполняет, когда оно движется.

Мы можем воспользоваться кинетической энергией многих природных явлений. Например, движение воды в реке превращается в электричество благодаря электростанциям. Энергия ветра – это кинетическая энергия воздуха. Когда мы прибиваем гвоздь молотком, мы используем кинетическую энергию молотка при его перемещении.

Кинетическая энергия в физике измеряется в джоулях , сокращенно буквой J.

Формула кинетической энергии

Для расчета кинетической энергии тел используется уравнение:

Это означает, что кинетическая энергия Ec равна массе тела m, умноженной на квадрат скорости v, делённые на 2.

Мы можем сделать вывод, что чем больше масса, тем больше энергия, и что энергия пропорциональна скорости, умноженной на себя.

Кинетическая энергия не является вектором. Это означает, что если вы бросаете шар со скоростью 5 м / с, шар будет иметь одинаковую кинетическую энергию, независимо от того, бросаете ли вы его влево или вправо или вверх.

Кинетическая энергия зависит от массы и скорости

Гоночные машины спроектированы с наименьшей массой для улучшения характеристик.

Кинетическая энергия зависит от массы и скорости тела. Это означает, что чем больше или быстрее объект, тем больше энергии он производит.

Примером вышесказанного может быть следующее: грузовик больше, чем автомобиль; Если оба едут с одинаковой скоростью и врезаются в стену, урон, нанесенный грузовиком, будет больше. В этом случае грузовик обладает большей кинетической энергией.

А теперь представьте: две одинаковые машины едут, одна со скоростью 50 км / ч, а другая со скоростью 100 км / ч. Чем выше скорость, тем серьезнее авария.

Таким образом, кинетическая энергия зависит от квадрата скорости. Это означает, что когда скорость объекта удваивается, его кинетическая энергия увеличивается в четыре раза.

Автомобиль, движущийся со скоростью 60 км / ч, имеет в четыре раза больше кинетической энергии, чем автомобиль, движущийся со скоростью 30 км / ч, и, следовательно, в четыре раза больший потенциал разрушения в случае аварии.

Как рассчитать кинетическую энергию тела?

В аэропорту хотят рассчитать кинетическую энергию 30-килограммовой упаковки в системе, которая движется со скоростью 0,500 м / с. Как мы это делаем?

Мы знаем массу и скорость упаковки, поэтому используем формулу:
Подставляя значения, имеем:

Рассуждение

Единицей кинетической энергии является джоуль, которая является той же для единицы работы

Обратите внимание, что, несмотря на то, что он тяжелый, его кинетическая энергия не так велика из-за его низкой скорости

Ключевые моменты для запоминания

Тело имеет кинетическую энергию, только если оно находится в движении.
Кинетическая энергия зависит от массы и скорости тела.

Задача 1 на нахождение кинетической энергии

Слон в 6000 кг бежит со скоростью 10 м / с. Какова его кинетическая энергия? Какова скорость пушечного ядра весом 1 кг, если у него была та же самая кинетическая энергия слона?

Ответ

Используя уравнение кинетической энергии, энергия слона равна:

Рассчитав кинетическую энергию, мы можем получить скорость пули, очистив v:

Это означает, что скорость пули равна 775 м / с. Сравните это со скоростью слона: вот это разница!

Задача 2

Мужчина врезался в столб на своей машине. Когда он пошел, чтобы сообщить о катастрофе, он сказал, что ехал с допустимой скоростью во время аварии.

Но следователь помнил физику 7 и 8 класса и установил, что скорость транспортного средства была в два раза выше, чем утверждал водитель.

Какова взаимосвязь между кинетической энергией и скоростью, сообщаемой человеком, и кинетической энергией со скоростью, рассчитанной следователем?

Мы будем рассматривать Ec1 как кинетическую энергию транспортного средства на скорости v1, сообщаемой человеком, и Ec2 как кинетическую энергию со значением скорости v2, рассчитанным исследователем. Соотношение между кинетическими энергиями рассчитывается путем деления энергий следующим образом:

Следователь сказал, что скорость во время аварии была вдвое выше, чем сообщал человек, то есть:
Подставим значение скорости в уравнение:

Исключая похожие термины, мы имеем:

Это означает, что кинетическая энергия в соответствии со скоростью, сообщаемой человеком, составляет четверть кинетической энергии по расчетам следователя. Проще говоря, ущерб, нанесенный автомобилем, был в четыре раза больше, чем сообщал мужчина.

Максимальная кинетическая энергия груза на пружине

Свободные колебания совершаются под действием внутренних сил системы после того, как система была выведена из положения равновесия.

Для того, чтобы свободные колебания совершались по гармоническому закону, необходимо, чтобы сила, стремящаяся возвратить тело в положение равновесия, была пропорциональна смещению тела из положения равновесия и направлена в сторону, противоположную смещению:

В этом соотношении ω – круговая частота гармонических колебаний. Таким свойством обладает упругая сила в пределах применимости закона Гука:

Силы любой другой физической природы, удовлетворяющие этому условию, называются квазиупругими .

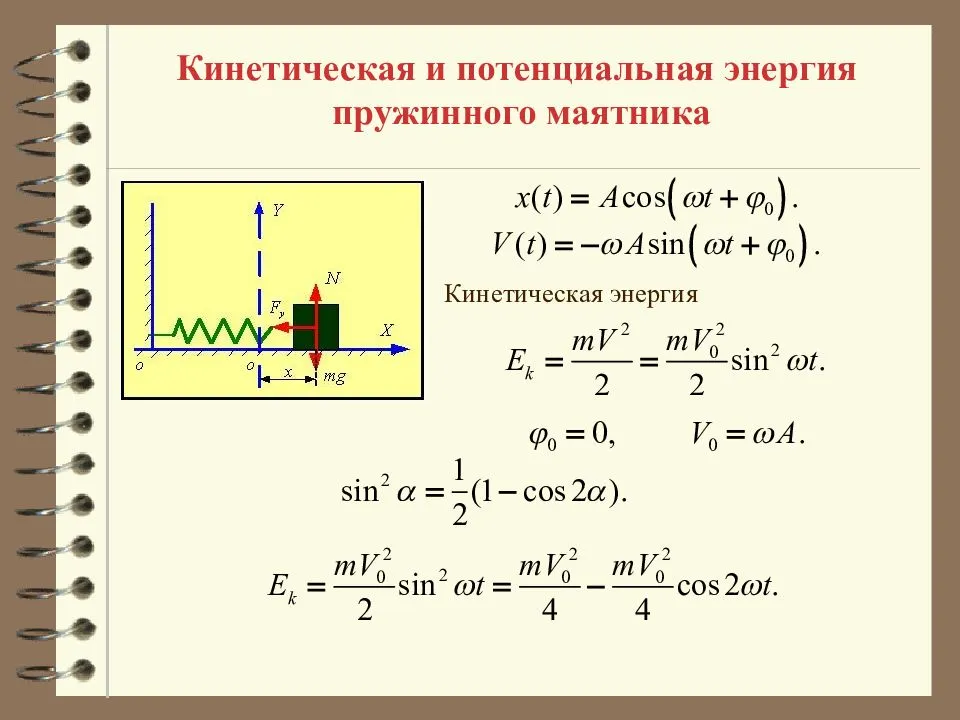
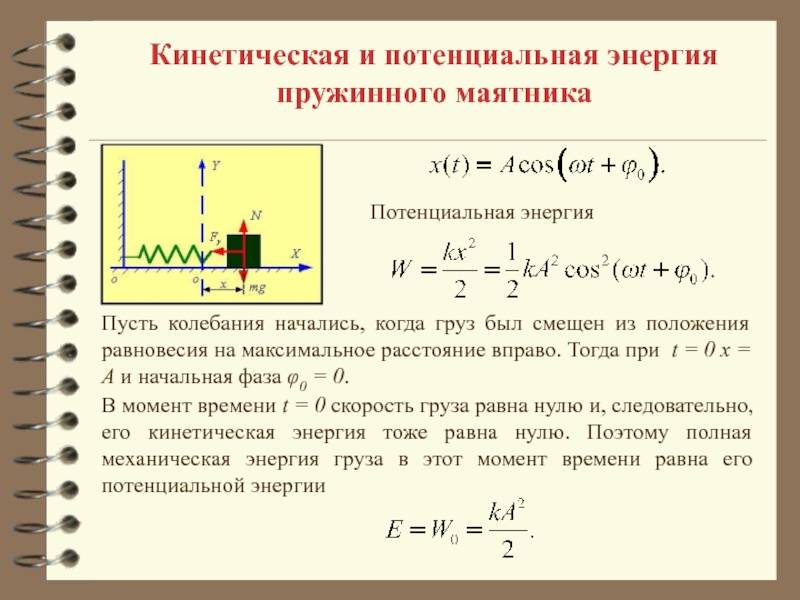
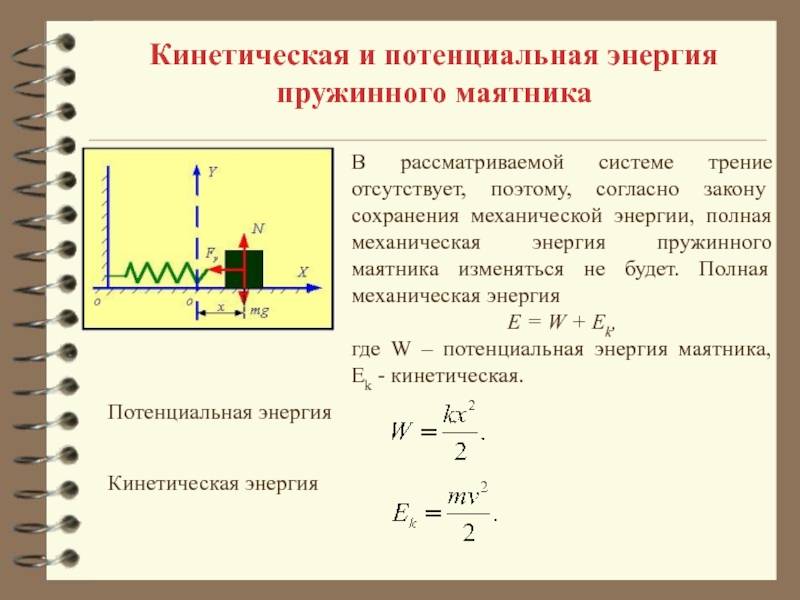
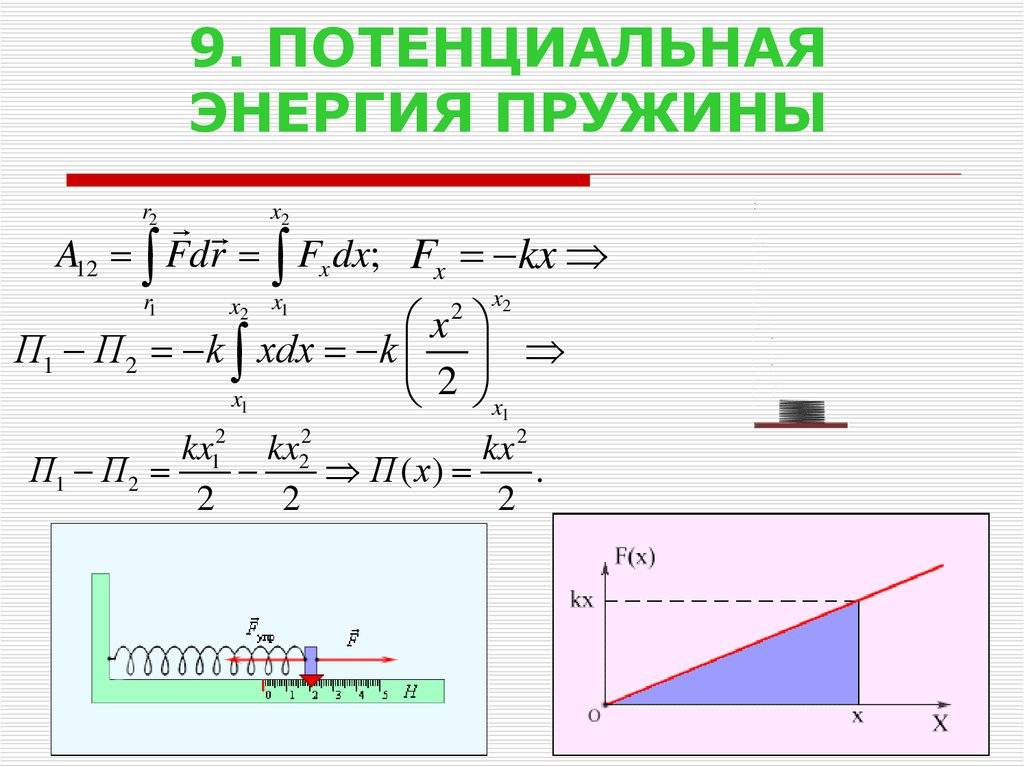
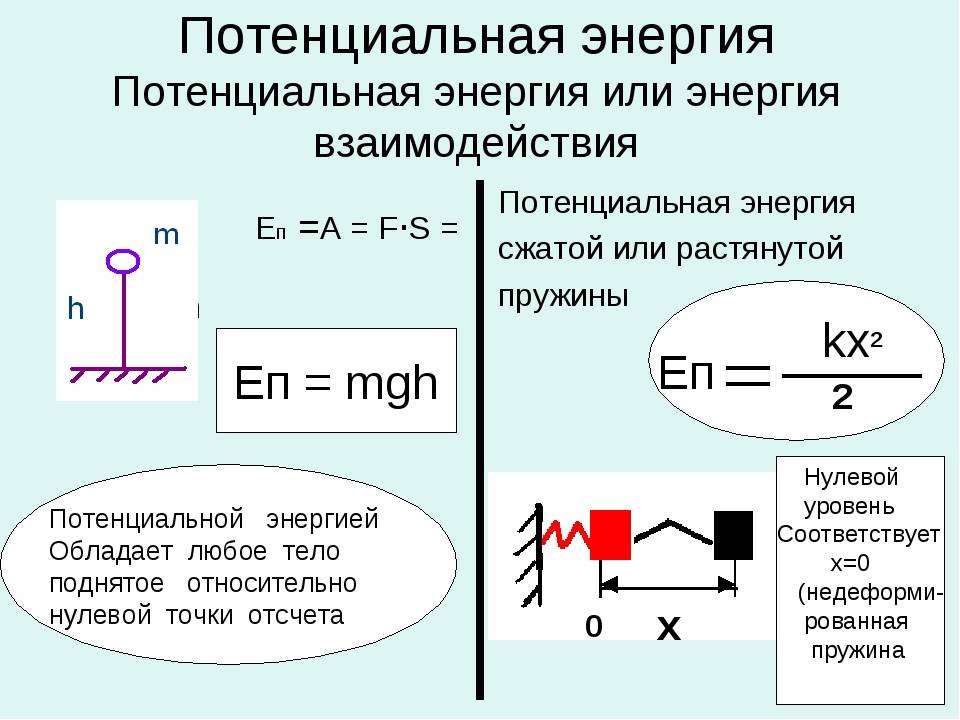
При свободных механических колебаниях кинетическая и потенциальная энергии изменяются периодически. При максимальном отклонении тела от положения равновесия его скорость, а следовательно, и кинетическая энергия обращаются в нуль. В этом положении потенциальная энергия колеблющегося тела достигает максимального значения. Для груза на горизонтально расположенной пружине потенциальная энергия – это энергия упругих деформаций пружины.

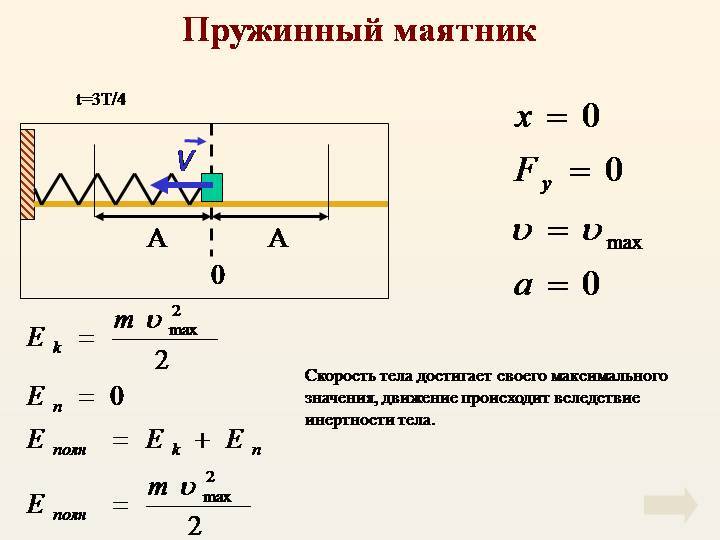
Когда тело при своем движении проходит через положение равновесия, его скорость максимальна. В этот момент оно обладает максимальной кинетической и минимальной потенциальной энергией. Увеличение кинетической энергии происходит за счет уменьшения потенциальной энергии. При дальнейшем движении начинает увеличиваться потенциальная энергия за счет убыли кинетической энергии и т. д.

Таким образом, при гармонических колебаниях происходит периодическое превращение кинетической энергии в потенциальную и наоборот.

Если в колебательной системе отсутствует трение, то полная механическая энергия при свободных колебаниях остается неизменной.

Для груза на пружине:

Запуск колебательного движения тела осуществляется с помощью кнопки Старт . Остановить процесс в любой момент времени позволяет кнопка Стоп .

Графически показано соотношение между потенциальной и кинетической энергиями при колебаниях в любой момент времени

Обратите внимание, что в отсутствие затухания полная энергия колебательной системы остается неизменной, потенциальная энергия достигает максимума при максимальном отклонении тела от положения равновесия, а кинетическая энергия принимает максимальное значение при прохождении тела через положение равновесия

Задание 7. Верхний конец пружины идеального пружинного маятника неподвижно закреплён, как показано на рисунке. Масса груза маятника равна m, жёсткость пружины равна k. Груз оттянули вниз на расстояние x от положения равновесия и отпустили с начальной скоростью, равной нулю. Формулы А и Б позволяют рассчитать значения физических величин, характеризующих колебания маятника.

Установите соответствие между формулами и физическими величинами, значение которых можно рассчитать по этим формулам.

К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.

1) амплитуда колебаний скорости

2) циклическая частота колебаний

3) максимальная кинетическая энергия груза

4) период колебаний

А) Имеем пружинный маятник массой m и жесткостью пружины k, тогда период свободных колебаний этого маятника определяется по формуле

Б) Для пружинного маятника известны формулы кинетической энергии

Пружинный маятник, состоящий из груза и лёгкой пружины, совершает колебания. В момент, когда груз находится в крайнем положении, его немного подталкивают вдоль оси пружины в направлении от положения

равновесия. Как в результате этого изменяются максимальная кинетическая энергия груза маятника и частота его колебаний?

Для каждой величины определите соответствующий характер изменения:

3) не изменяется

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Максимальная кинетическая энергия груза маятника

Частота колебаний маятника

Груз подтолкнули от положения равновесия, откуда следует, что амплитуда колебаний груза увеличится. При этом увеличится также и максимальная потенциальная энергия пружины. По закону сохранения энергии, это приведет к увеличению максимальной кинетической энергии груза маятника.

Период и частота пружинного маятника зависят только от массы груза и жесткости пружины. Таким образом, при увеличении амплитуды колебаний груза, частота колебаний маятника не изменится.

Гармонические колебания пружинного маятника

В 1985 году в городе Мехико произошла ужасная катастрофа, причина которой было землетрясение: 5526 человек погибли, 40 ООО человек ранены, 31000 человек остались без крова. Из проведенных затем исследований ученые выяснили, что главной причиной разрушений во время землетрясения является совпадение частоты свободных колебаний зданий с частотой вынужденных колебаний Земли. Поэтому при возведении новых зданий в сейсмически активной зоне необходимо, чтобы эти частоты не совпадали. Это даст возможность уменьшить последствия землетрясения

С этой целью важно знать, от чего зависят частота и период колебаний

Одной из простейших колебательных систем, совершающих гармонические колебания, является пружинный маятник.

Пружинный маятник — это колебательная система, состоящая из пружины и закрепленного на ней тела. Колебания, возникающие в пружинном маятнике, являются гармоническими колебаниями:

Под гармоническими колебаниями подразумеваются колебания, возникающие под действием силы, прямо пропорциональной перемещению и направленной против направления перемещения.

Исследование колебаний пружинного маятника имеет большое практическое значение, например, при вычислении колебаний рессор автомобиля при езде; в исследовании воздействия колебаний на фундамент зданий и тяжелых станков, в определении эластичности ушных перепонок при диагностике лор-заболеваний. По этой причине изучение колебаний пружинного маятника является актуальной проблемой.

С целью уменьшения количества сил, действующих на колебательную систему, целесообразно использовать горизонтально расположенную колебательную систему пружина-шарик (d).

В этой системе действия силы тяжести и реакции опоры уравновешивают друг друга. При выведении шарика из состоянии равновесия, например, при растяжении пружины до положения сила упругости, возникающая в ней, сообщает шарику ускорение и приводит его в колебательное движение. По II закону Ньютона уравнение движения маятника можно записать так:

или

Формула (4.9) является уравнением свободных гармонических колебаний пружинного маятника.

Где – масса шарика, закрепленного на пружине, — проекция ускорения шарика вдоль оси — жесткость пружины, -удлинение пружины, равное амплитуде колебания. Для данной колебательной системы отношение – постоянная положительная величина (так как масса и жесткость не могут быть отрицательными). При сравнении уравнения колебаний (4.9) пружинного маятника с выражением для другого вида периодического движения – известным выражением центростремительного ускорения при равномерном движении по окружности получается, что отношение соответствует квадрату циклической частоты

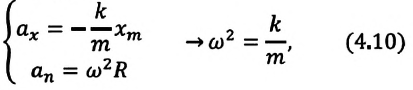
или

Таким образом, уравнение движения пружинного маятника можно записать и так:

Уравнение (4.12) показывает, что колебания пружинного маятника с циклической частотой являются свободными гармоническими колебаниями. Из математики известно, что решением этого уравнения является:

Так как тригонометрическая функция является гармонической функцией, то и колебания пружинного маятника являются гармоническими колебаниями.

Здесь фаза колебания, — начальная фаза. Единица измерения фазы в СИ – радиан (1 рад). Фазу также можно измерять в градусах: Значение начальной фазы зависит от выбора начального момента времени. Начальный момент времени можно выбрить так, чтобы В этом случае формулу гармонических колебаний пружинного маятника можно записать так:

или

Из сравнения выражений (4.11) и (4.5) определяются величины, от которых зависят период и частота колебаний пружинного маятника:

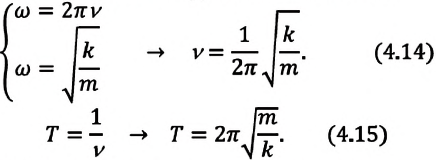
Из выражений (4.14) и (4.15) видно, что период и частота пружинного маятника зависят от жесткости пружины и массы груза, подвешенного к нему.

Закон сохранения энергии

В физике и правда ничего не исчезает бесследно. Чтобы это как-то выразить, используют законы сохранения. В случае с энергией — Закон сохранения энергии.

Закон сохранения энергии

Полная механическая энергия замкнутой системы остается постоянной.

Полная механическая энергия — это сумма кинетической и потенциальной энергий. Математически этот закон описывается так:

Закон сохранения энергии

Е_{полн. мех.} = Е_п + E_к = const

Е_{полн. мех.} — полная механическая энергия системы

Е_п — потенциальная энергия

Е_к — кинетическая энергия

const — постоянная величина

Задачка раз

Мяч бросают вертикально вверх с поверхности Земли. Сопротивление воздуха пренебрежимо мало. Как изменится высота подъёма мяча при увеличении начальной скорости мяча в 2 раза?

Решение:

Должен выполняться закон сохранения энергии:

В начальный момент времени высота равна нулю, значит Е_п = 0. В этот же момент времени Е_к максимальна.

В конечный момент времени все наоборот — кинетическая энергия равна нулю, так как мяч уже не может лететь выше, а вот потенциальная максимальна, так как мяч докинули до максимальной высоты.

Это можно описать соотношением:

Е_п1 + Е_к1 = Е_п2 + Е_к2

0 + Е_к1 = Е_п2 + 0

Е_к1 = Е_п2

Разделим на массу левую и правую часть

Из соотношения видно, что высота прямо пропорциональна квадрату начальной скорости, значит при увеличении начальной скорости мяча в два раза, высота должна увеличиться в 4 раза.

Ответ: высота увеличится в 4 раза

Задачка два

Тело массой m, брошенное с поверхности земли вертикально вверх с начальной скоростью v, поднялось на максимальную высоту h. Сопротивление воздуха пренебрежимо мало. Чему будет равна полная механическая энергия тела на некоторой промежуточной высоте h?

Решение

По закону сохранения энергии полная механическая энергия изолированной системы остаётся постоянной. В максимальной точке подъёма скорость тела равна нулю, а значит, оно будет обладать исключительно потенциальной энергией Е_мех = Е_п = mgh.

Таким образом, на некоторой промежуточной высоте h, тело будет обладать и кинетической и потенциальной энергией, но их сумма будет иметь значение Е_мех = mgh.

Ответ: Е_мех = mgh.

Задачка три

Мяч массой 100 г бросили вертикально вверх с поверхности земли с начальной скоростью 6 м/с. На какой высоте относительно земли мяч имел скорость 2 м/с? Сопротивлением воздуха пренебречь.

Решение:

Переведем массу из граммов в килограммы:

m = 100 г = 0,1 кг

У поверхности земли полная механическая энергия мяча равна его кинетической энергии:

Дж

На высоте h потенциальная энергия мяча есть разность полной механической энергии и кинетической энергии:

Дж

м

Ответ: мяч имел скорость 2 м/с на высоте 1,6 м

Виды пружин

Видов этих деталей существует много, самыми распространенными являются пружины растяжения и сжатия.

Первые из них без нагрузки имеют нулевой шаг, то есть виток соприкасается с витком. В процессе деформации они растягиваются, их длина увеличивается. Прекращение нагрузки сопровождается возвращением в первоначальную форму – опять витком к витку.
Вторые – наоборот, изначально навиваются с определенным шагом между витками, под нагрузкой сжимаются. Соприкосновение витков является естественным ограничителем для продолжения воздействия.

Изначально именно для пружины растяжения было найдено соотношение массы подвешенного на ней груза и изменения ее геометрического размера, которое и стало основой для формулы жесткости пружины через массу и длину.

Какие еще бывают виды пружин

Зависимость деформации от прилагаемой внешней силы справедлива и для других видов упругих деталей: кручения, изгиба, тарельчатых, других

Не важно, в какой плоскости к ним прилагаются усилия: в той, где расположена осевая линия, или перпендикулярной к ней, производимая деформация пропорциональна усилию, под воздействием которого она произошла