Пружинный маятник: амплитуда колебаний, период, формула

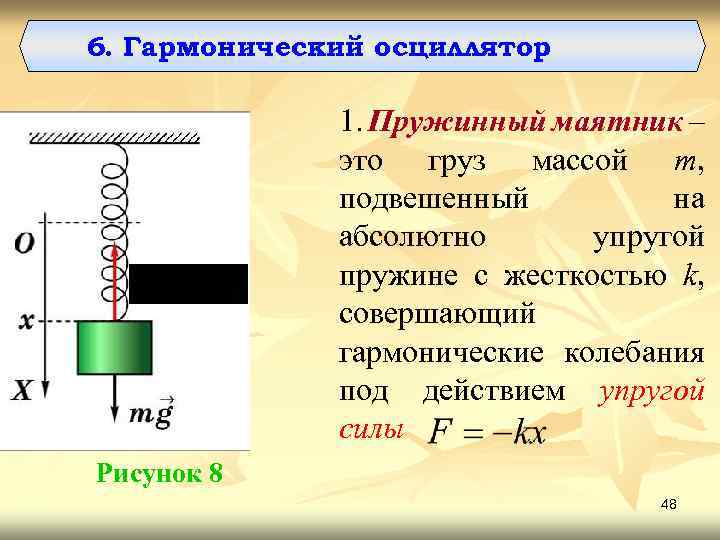
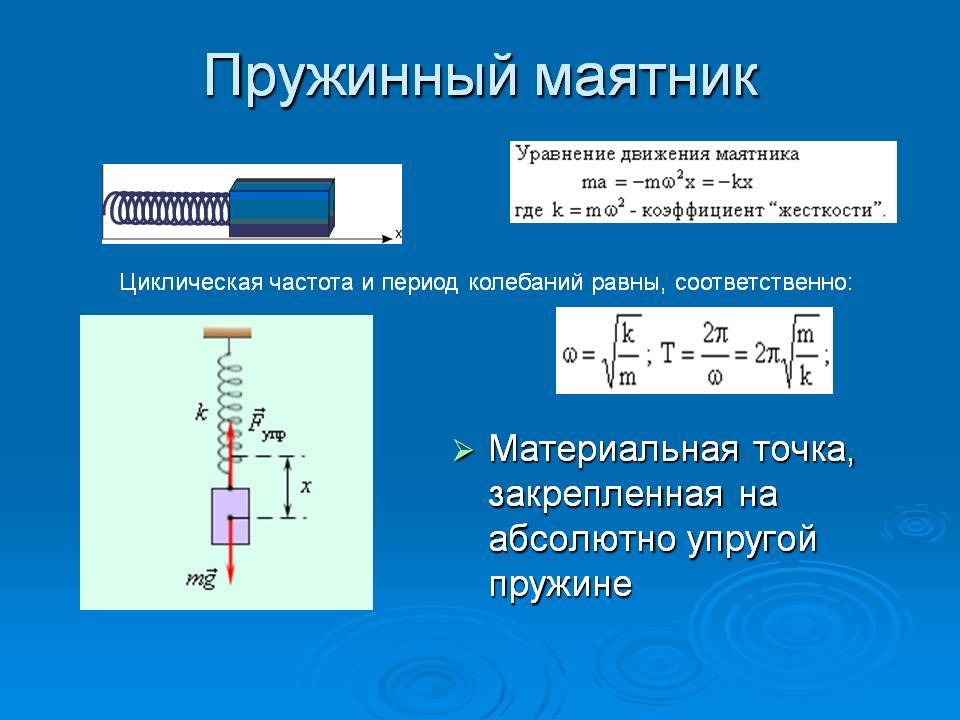
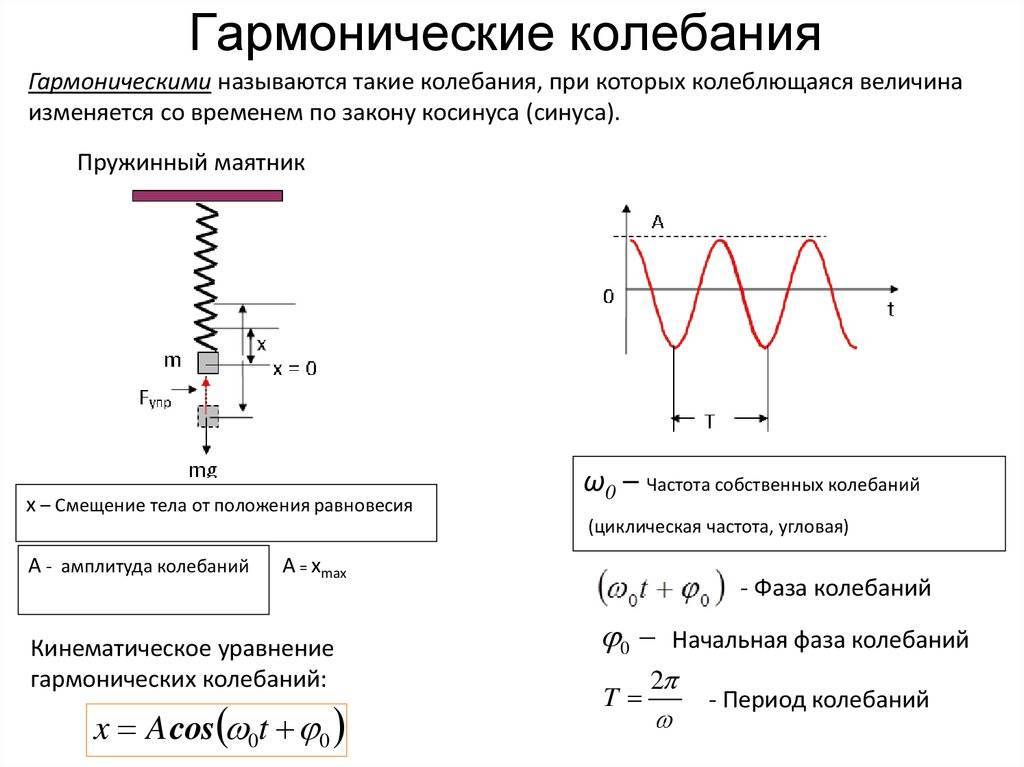
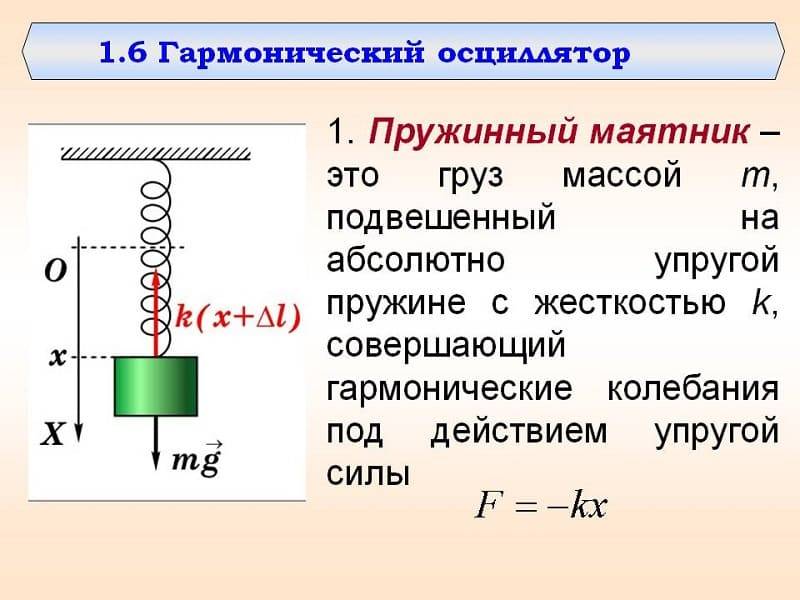
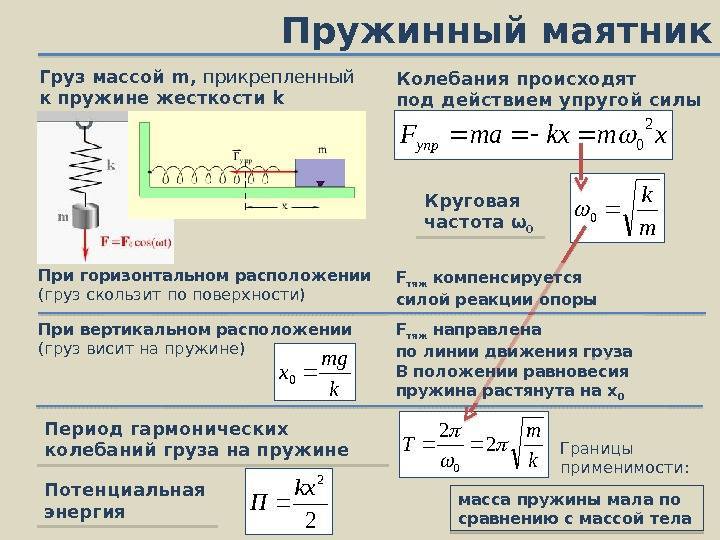
Характеристики колебаний

Чтобы перейти к гармоническим колебаниям, нам нужно описать величины, которые помогут нам эти колебания охарактеризовать. Любое колебательное движение характеризуется величинами: период, частота, амплитуда, фаза колебаний.

Формула периода колебаний T = t/N T — период t — время N — количество колебаний

Также есть величина, обратная периоду — частота. Она показывает, сколько колебаний совершает система в единицу времени.

Формула частоты ν = N/t = 1/T ν — частота t — время T — период N — количество колебаний

Амплитуда — это максимальное отклонение от положения равновесия. Измеряется в метрах и обозначается либо буквой A, либо xmax.

Она используется в уравнении гармонических колебаний:

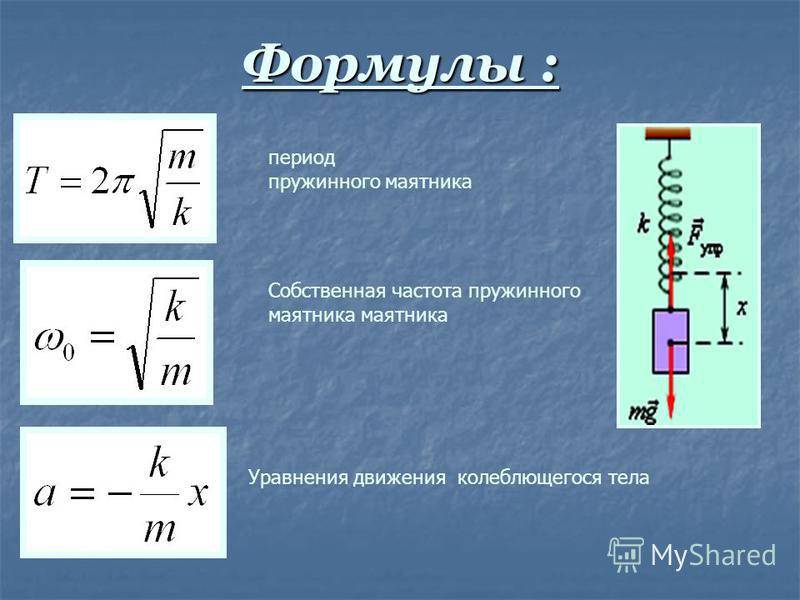
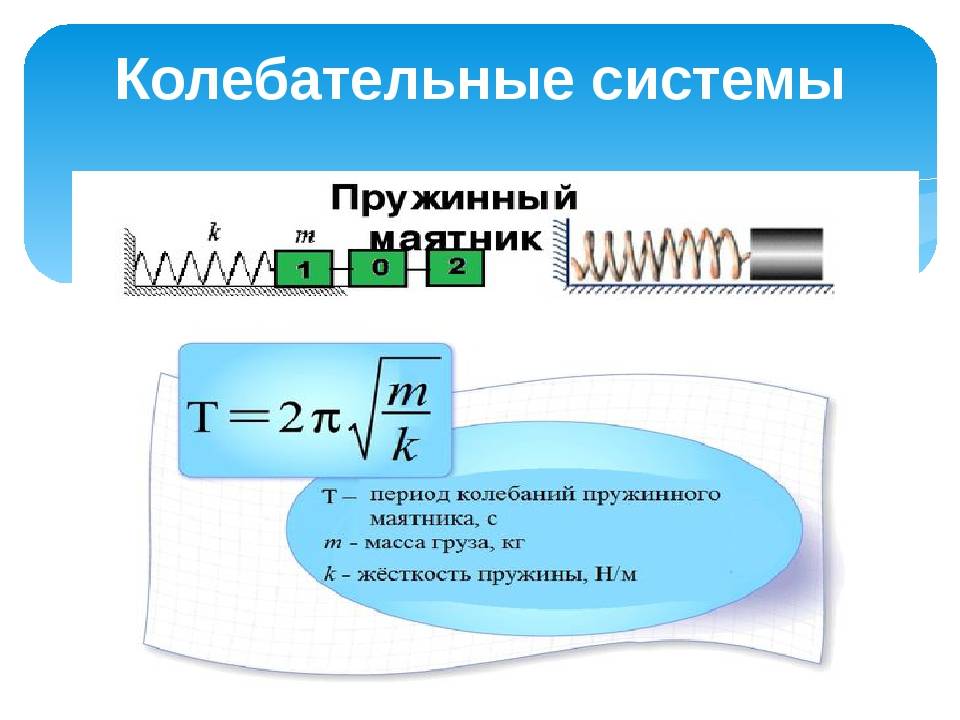
Формула для расчета периода колебаний пружинного маятника

• Механика (56)
  • Кинематика (19)
  • Динамика и статика (32)
  • Гидростатика (5)
• Молекулярная физика (25)
  • Уравнение состояния (3)
  • Термодинамика (15)
  • Броуновское движение (6)
  • Прочие формулы по молекулярной физике (1)
• Колебания и волны (22)
• Оптика (9)
  • Геометрическая оптика (3)
  • Физическая оптика (5)
  • Волновая оптика (1)
• Электричество (39)
• Атомная физика (15)
• Ядерная физика (3)

• Квадратный корень, рациональные переходы (1)
• Квадратный трехчлен (1)
• Координатный метод в стереометрии (1)
• Логарифмы (1)
• Логарифмы, рациональные переходы (1)
• Модуль (1)
• Модуль, рациональные переходы (1)
• Планиметрия (1)
• Прогрессии (1)
• Производная функции (1)
• Степени и корни (1)
• Стереометрия (1)
• Тригонометрия (1)
• Формулы сокращенного умножения (1)

Сообщение от администратора:

Ребята! Кто давно хотел выучить английский?Переходите по моей ссылке и получите два бесплатных урока в школе английского языка SkyEng! Занимаюсь там сам — очень круто. Прогресс налицо.

В приложении можно учить слова, тренировать аудирование и произношение.

Попробуйте. Два урока бесплатно по моей ссылке! Жмите СЮДА

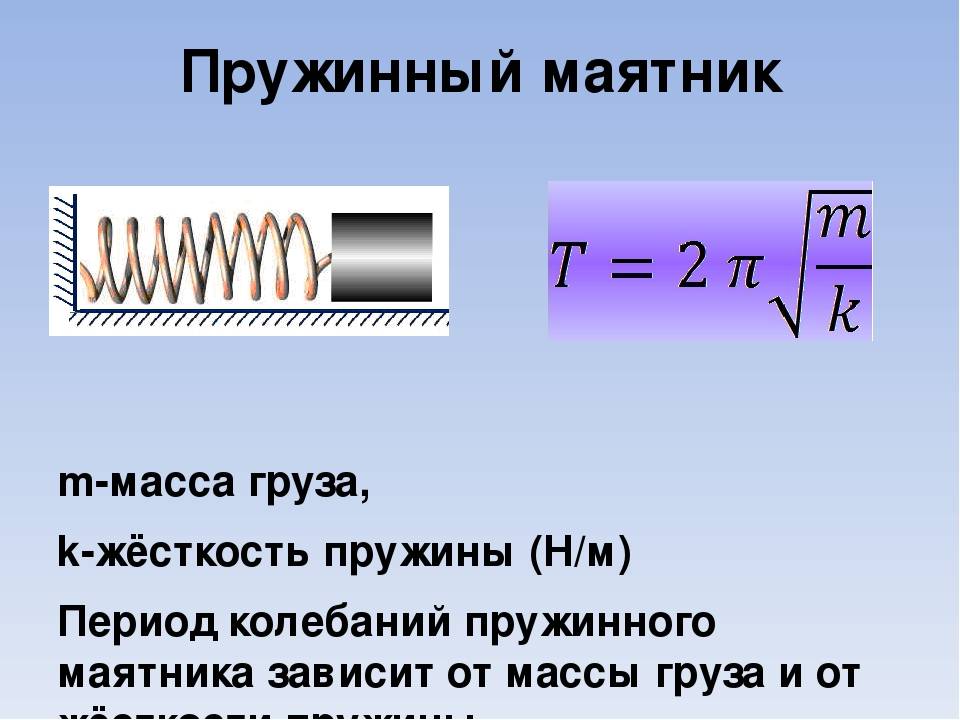
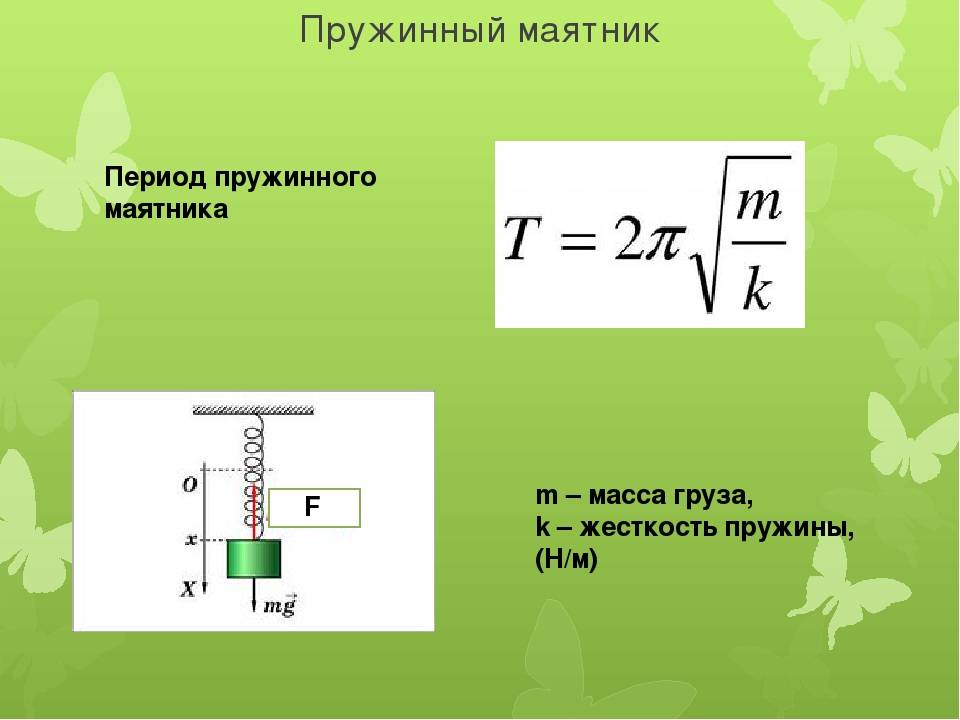
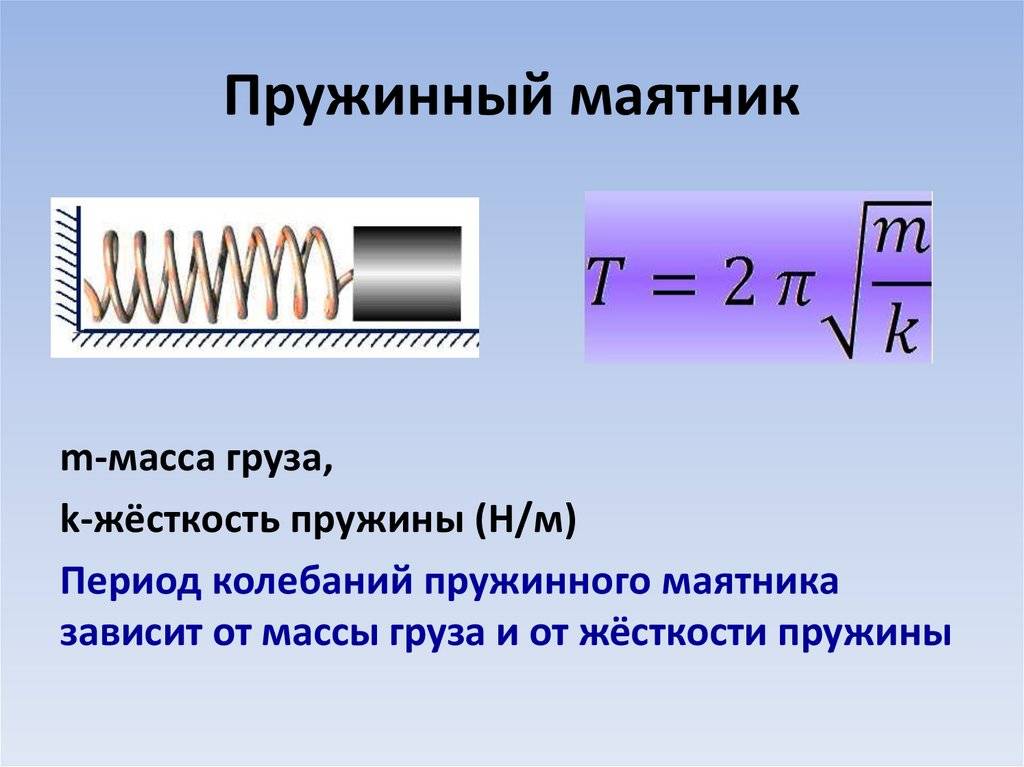
Период пружинного маятника — зависит от жёсткости пружины: с увеличением коэффициента жёсткости пружины период колебания маятника уменьшается

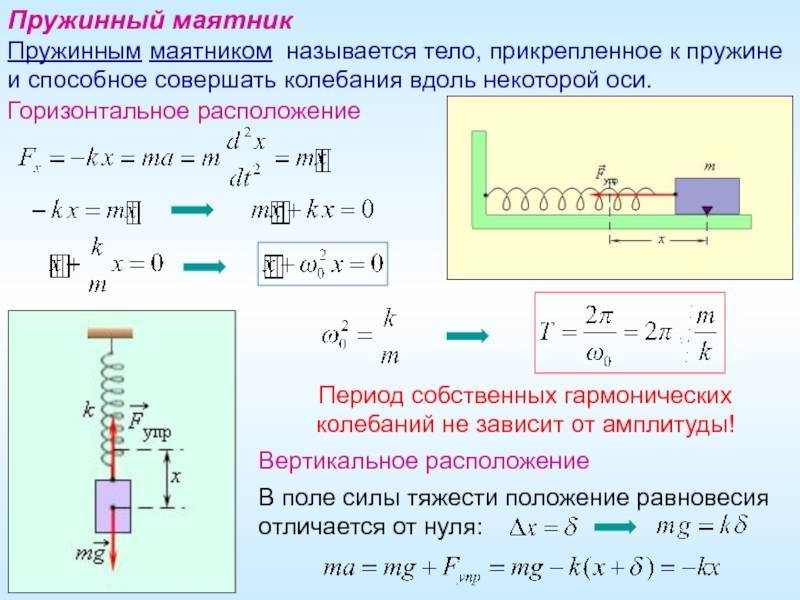
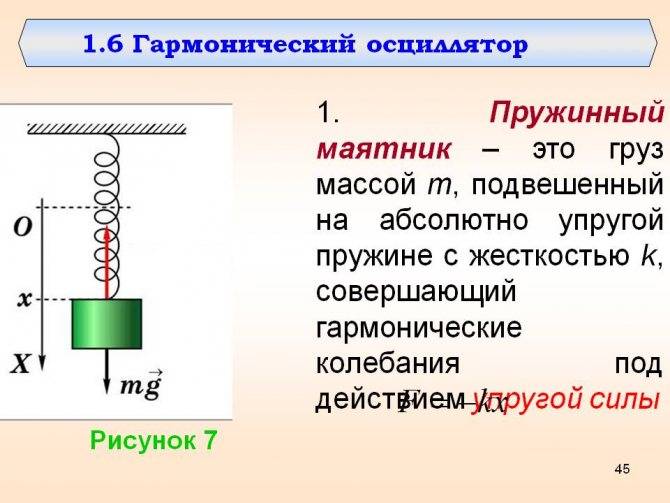
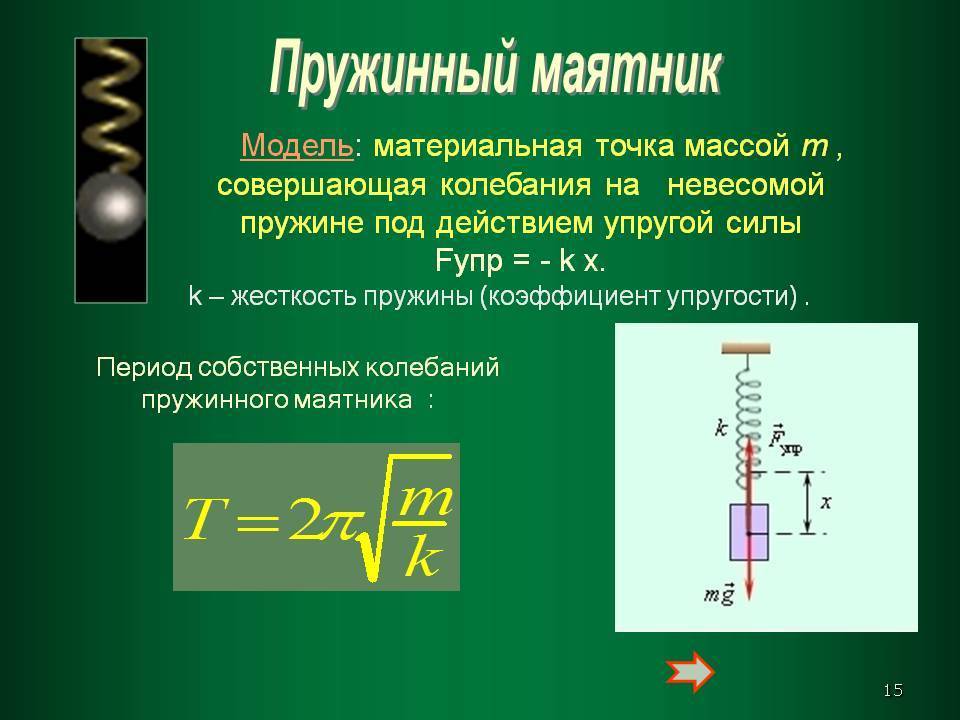
Пружинный маятник — это груз, колеблющийся на пружине. Он совершает возвратно-поступательное движение. Пружинный маятник подчиняется законам движения, по которым можно определить период его колебаний, зная массу груза и жесткость пружины. Период колебаний пружинного маятника не зависит от места его расположения и амплитуды колебаний.

Давайте выведем формулу периода пружинного маятника.

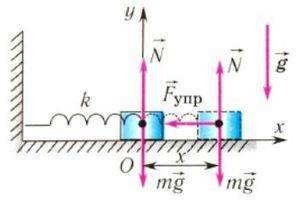
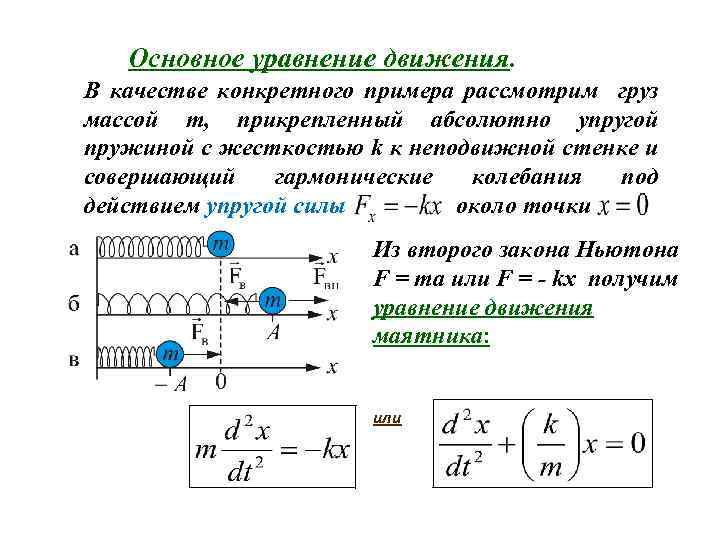
На груз m горизонтального пружинного маятника действуют сила тяжести (mg), сила реакции опоры (N) и сила упругости пружины (Fynp). Запишем второй закон Ньютона для данного случая :

Все проецируем на ось ОХ:

Запишем это уравнение в форме аналогичной уравнению движения гармонического осциллятора:

Сравнивая полученное выражение с уравнением гармонических колебаний у нас получается:

Из уравнения видно, что циклическая частота пружинного маятника будет иметь вид:

Тогда период колебаний пружинного маятника будет равен:

• Период физического маятника
• Период крутильного маятника
• В Формуле мы использовали :
• — Период пружинного маятника маятника
• — Масса груза
• — Изменение длины пружины
• — Коэффициент упругости пружины
• — Ускорение свободного падения
• — Циклическая частота пружинного маятника
• — Сила реакции опоры
• — Сила упругости

Формула периода колебаний пружинного маятника

1. Период — это минимальное время, за которое совершается одно полное колебательное движение.
2. Обозначают период буквой $T$.
3. где $Delta t$ — время колебаний; $N$ — число полных колебаний.

Уравнение колебаний пружинного маятника

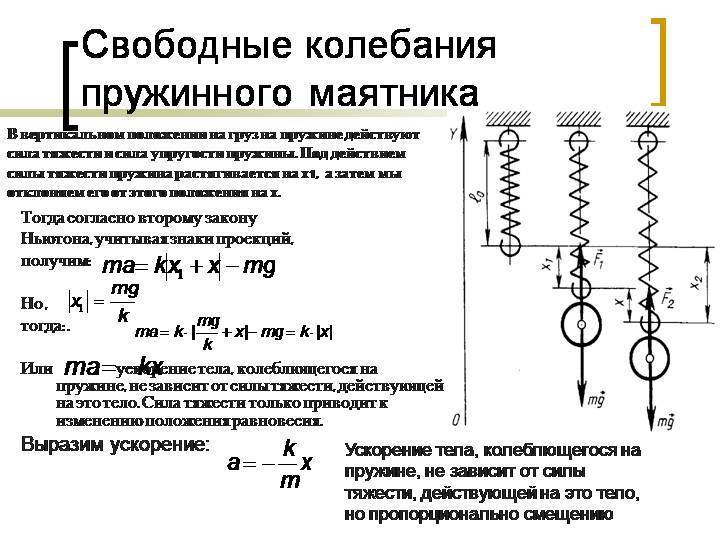
Рассмотрим простейшую колебательную систему, в которой можно реализовать механические колебания. Это груз массы $m$, подвешенный на пружине, коэффициент упругости которой равен $k $(рис.1).

Рассмотри вертикальное движение груза, которое обусловлено действием силы тяжести и силы упругости пружины. В состоянии равновесия такой системы, сила упругости равна по величине силе тяжести.

Допустим, что масса пружины мала в сравнении с массой груза, при описании колебаний ее учитывать не будем. Началом отсчета будем считать точку на оси координат (X), которая совпадает с положением равновесия груза. В этом положении пружина уже имеет удлинение, которое обозначим $b$. Растяжение пружины происходит из-за действия на груз силы тяжести, следовательно:

• Если груз смещают дополнительно, но закон Гука еще выполняется, то сила упругости пружины становится равна:
• Ускорение груза запишем, помня, что движение происходит по оси X, как:
• Второй закон Ньютона для груза принимает вид:
• Учтем равенство (2), формулу (5) преобразуем к виду:
• Если ввести обозначение: $^2_0=frac$, то уравнение колебаний запишем как:
• где $^2_0=frac$ — циклическая частота колебаний пружинного маятника. Решением уравнения (7) (это проверяется непосредственной подстановкой) является функция:
• где $_0=sqrt>0$- циклическая частота колебаний маятника, $A$ — амплитуда колебаний; $_0t+varphi )$ — фаза колебаний; $varphi $ и $_1$ — начальные фазы колебаний.

Звук

Звук – это колебания упругой среды, воспринимаемые органом слуха.

Условия, необходимые для возникновения и ощущения звука:

• наличие источника звука;
• наличие упругой среды между источником и приемником звука;
• наличие приемника звука; • частота колебаний должна лежать в звуковом диапазоне;
• мощность звука должна быть достаточной для восприятия.

Звуковые волны – это упругие волны, вызывающие у человека ощущение звука, представляющие собой зоны сжатия и разряжения, передающиеся на расстояние с течением времени.

Классификация звуковых волн:

• инфразвук (​\( \nu \)​ < 16 Гц);
• звуковой диапазон (16 Гц < \( \nu \) < 20 000 Гц);
• ультразвук (\( \nu \) > 20 000 Гц).

Скорость звука – это скорость распространения фазы колебания, т. е. области сжатия и разряжения среды.

Скорость звука зависит

от упругих свойств среды:

в воздухе – 331 м/с, в воде – 1400 м/с, в металле – 5000 м/с;

от температуры среды:

в воздухе при температуре 0°С – 331 м/с, в воздухе при температуре +15°С – 340 м/с.

Характеристики звуковой волны

• Громкость – это величина, характеризующая слуховые ощущения человека, зависящая от амплитуды колебаний в звуковой волне. Единицы измерения – дБ (децибел).
• Высота тона – это величина, характеризующая слуховые ощущения человека, зависящая от частоты колебаний в звуковой волне. Чем больше частота, тем выше звук. Чем меньше частота, тем ниже звук.
• Тембр – это окраска звука.

Музыкальный звук – это звук, издаваемый гармонически колеблющимся телом. Каждому музыкальному тону соответствует определенная длина и частота звуковой волны.Шум – хаотическая смесь тонов.

Темы по физике

• Механика (56)
  • Кинематика (19)
  • Динамика и статика (32)
  • Гидростатика (5)
• Молекулярная физика (25)
  • Уравнение состояния (3)
  • Термодинамика (15)
  • Броуновское движение (6)
  • Прочие формулы по молекулярной физике (1)
• Колебания и волны (22)
• Оптика (9)
  • Геометрическая оптика (3)
  • Физическая оптика (5)
  • Волновая оптика (1)
• Электричество (39)
• Атомная физика (15)
• Ядерная физика (3)

Темы по математике

• Квадратный корень, рациональные переходы (1)
• Квадратный трехчлен (1)
• Координатный метод в стереометрии (1)
• Логарифмы (1)
• Логарифмы, рациональные переходы (1)
• Модуль (1)
• Модуль, рациональные переходы (1)
• Планиметрия (1)
• Прогрессии (1)
• Производная функции (1)
• Степени и корни (1)
• Стереометрия (1)
• Тригонометрия (1)
• Формулы сокращенного умножения (1)

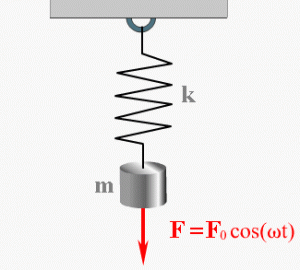
Вынужденные колебания

А вот вынужденные колебания восполняют запас энергии внешним воздействием. Если это происходит каждый период, то колебания вообще затухать не будут.

Вынужденные колебания — это колебания, которые происходят под действием внешней периодически меняющейся силы.

Частота, с которой эта сила воздействует, равна частоте, с которой система будет колебаться.

Например, качели. Если вас кто-то будет на них качать, каждый раз давая толчок, когда вы приходите в одну и ту же точку — такое колебание будет считаться вынужденным.

Это колебание все еще будет считаться вынужденным, если вас будут раскачивать из положения равновесия. Просто в данном случае амплитуда (о которой речь пойдет чуть ниже) будет увеличиваться с каждым колебанием.

Без лишних колебаний запишите ребенка на вводное занятие по физике в онлайн-школу Skysmart. Ученики занимаются на интерактивной платформе, в комфортном темпе и с внимательными учителями.

Никаких скучных заданий! Вместо этого — захватывающие примеры из жизни, вдохновение и поддержка.

Презентация на тему: ” И ССЛЕДОВАНИЕ ЗАВИСИМОСТИ ПЕРИОДА КОЛЕБАНИЙ ПРУЖИННОГО МАЯТНИКА ОТ МАССЫ ГРУЗА, ЖЁСТКОСТИ ПРУЖИНЫ, АМПЛИТУДЫ КОЛЕБАНИЙ И ТЕМПЕРАТУРЫ ВОЗДУХА. Работа учащихся.” — Транскрипт:

1

И ССЛЕДОВАНИЕ ЗАВИСИМОСТИ ПЕРИОДА КОЛЕБАНИЙ ПРУЖИННОГО МАЯТНИКА ОТ МАССЫ ГРУЗА, ЖЁСТКОСТИ ПРУЖИНЫ, АМПЛИТУДЫ КОЛЕБАНИЙ И ТЕМПЕРАТУРЫ ВОЗДУХА. Работа учащихся 9 класса МОУ «Старовыслинская ООШ» Шингалова Радия и Надукова Дениса 2011г. Учитель: Потапов Н.А.

2

Ц ЕЛЬ НАШЕЙ РАБОТЫ : Исследовать зависимость периода колебаний пружинного маятника от массы груза, жёсткости пружины, амплитуды колебаний и температуры воздуха.

3

В ВЕДЕНИЕ. В настоящее время в технике и быту используются различные виды пружины. Твердые тела и материалы, которыми располагает человечество, во многом определяет уровень его технического развития. Изучая свойства твердых тел, мы заинтересовались упругими свойствами пружины и решили исследовать их.

4

П ОДГОТОВКА К ЭКСПЕРИМЕНТУ Для проведения экспериментов подобрали следующее оборудование: штатив с 2-мя лапками, пружина 1 (к 1 =6,4 Н/м), пружина 2 (к 2 =21,6Н/м), набор грузов массой по 100г, линейка, секундомер, динамометр.

5

ПЕРИОД КОЛЕБАНИЯ Одной из важных характеристик колебательного движения является период колебания – интервал времени, в течение которого происходит одно полное колебание. Связь периода колебаний пружинного маятника от массы груза и жёсткости пружины известна:

6

П ЛАН ПРОВЕДЕНИЯ ЭКСПЕРИМЕНТА : Приготовить приборы и оборудования. Исследовать зависимость периода колебаний пружинного маятника от массы груза, жёсткости пружины, амплитуды и температуры воздуха. Заполнение таблиц измерений. Вычерчивание графиков зависимостей. Анализ графиков зависимостей периода от разных параметров. Обобщение результатов.

7

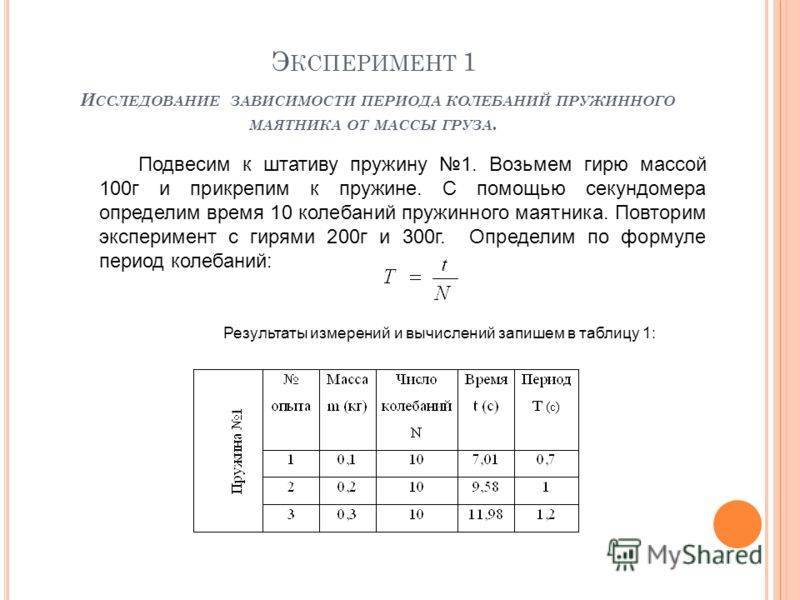
Э КСПЕРИМЕНТ 1 И ССЛЕДОВАНИЕ ЗАВИСИМОСТИ ПЕРИОДА КОЛЕБАНИЙ ПРУЖИННОГО МАЯТНИКА ОТ МАССЫ ГРУЗА. Подвесим к штативу пружину 1. Возьмем гирю массой 100г и прикрепим к пружине. С помощью секундомера определим время 10 колебаний пружинного маятника. Повторим эксперимент с гирями 200г и 300г. Определим по формуле период колебаний: Результаты измерений и вычислений запишем в таблицу 1:

8

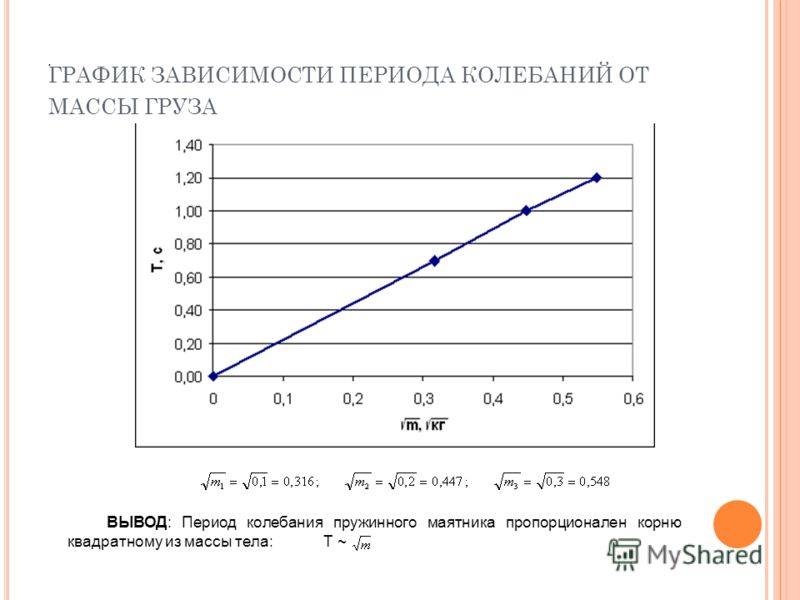
ГРАФИК ЗАВИСИМОСТИ ПЕРИОДА КОЛЕБАНИЙ ОТ МАССЫ ГРУЗА ВЫВОД: Период колебания пружинного маятника пропорционален корню квадратному из массы тела: Т ~.

9

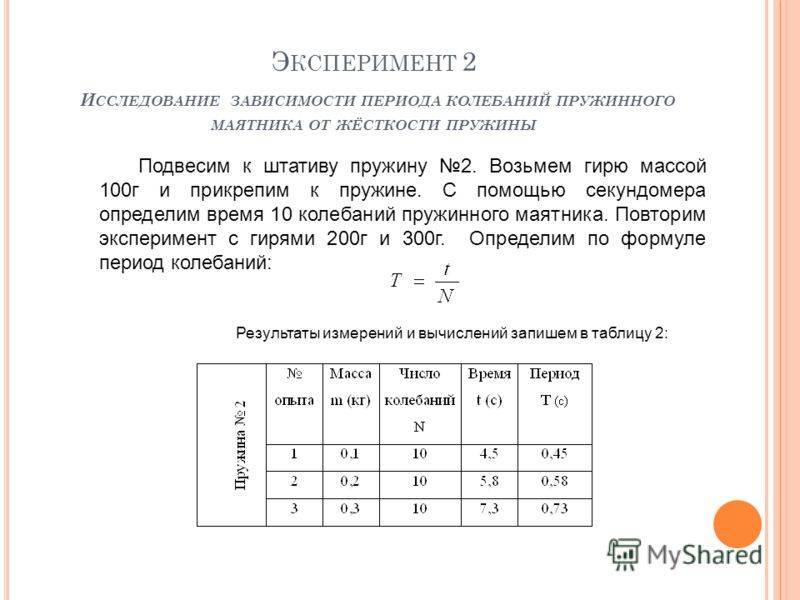
Э КСПЕРИМЕНТ 2 И ССЛЕДОВАНИЕ ЗАВИСИМОСТИ ПЕРИОДА КОЛЕБАНИЙ ПРУЖИННОГО МАЯТНИКА ОТ ЖЁСТКОСТИ ПРУЖИНЫ Подвесим к штативу пружину 2. Возьмем гирю массой 100г и прикрепим к пружине. С помощью секундомера определим время 10 колебаний пружинного маятника. Повторим эксперимент с гирями 200г и 300г. Определим по формуле период колебаний: Результаты измерений и вычислений запишем в таблицу 2:

10

ГРАФИК ЗАВИСИМОСТИ ПЕРИОДА КОЛЕБАНИЙ ОТ ЖЁСТКОСТИ ПРУЖИНЫ ВЫВОД : Период колебаний пружинного маятника зависит обратно пропорционально жесткости пружины:.

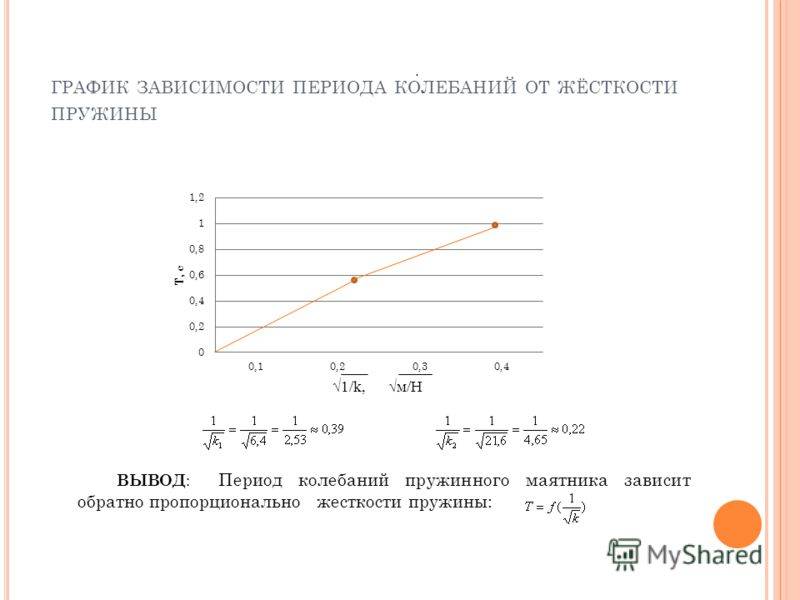
11

Э КСПЕРИМЕНТ 3 И ССЛЕДОВАНИЕ ЗАВИСИМОСТИ ПЕРИОДА КОЛЕБАНИЙ ПРУЖИННОГО МАЯТНИКА ОТ АМПЛИТУДЫ КОЛЕБАНИЙ Результаты измерений и вычислений запишем в таблицу 3: Не изменяя массы груза, жесткости пружины, установим зависимость периода колебаний от амплитуды. Повторим эксперимент 1 при разных амплитудах колебаний.

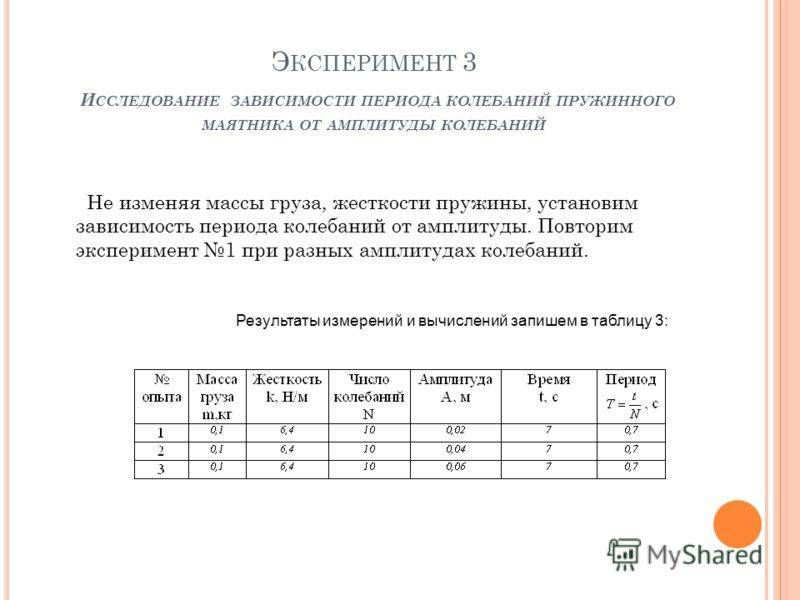
12

ГРАФИК ЗАВИСИМОСТИ ПЕРИОДА КОЛЕБАНИЙ ОТ АМПЛИТУДЫ КОЛЕБАНИЙ ВЫВОД: Эксперимент подтверждает, что период свободных колебаний пружинного маятника не зависит от амплитуды колебаний, а полностью определяется собственными характеристиками колебательной системы (жесткостью k и массой груза m).

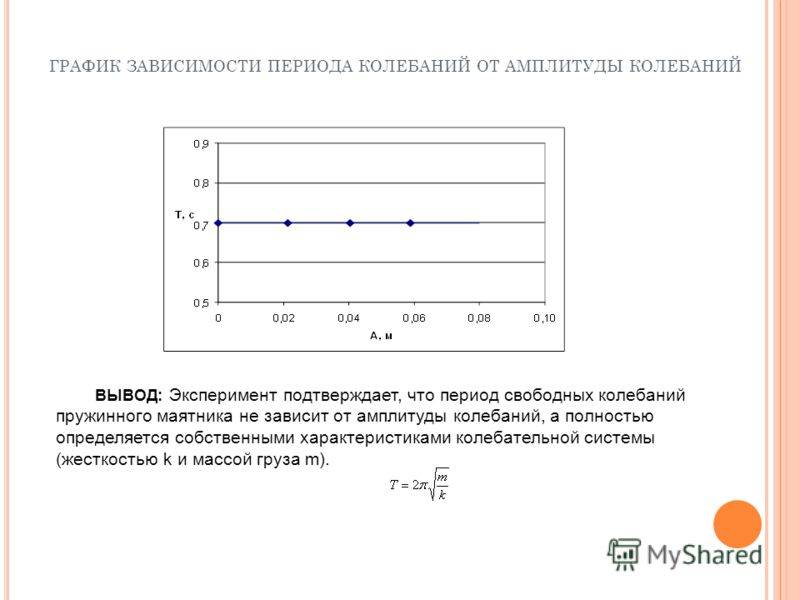
13

Э КСПЕРИМЕНТ 4 И ССЛЕДОВАНИЕ ЗАВИСИМОСТИ ПЕРИОДА КОЛЕБАНИЙ ПРУЖИННОГО МАЯТНИКА ОТ ТЕМПЕРАТУРЫ. Для исследования зависимости периода колебаний пружинного маятника от температуры повторили эксперимент 1 во дворе школы при другой температуре ( t= -20 0С ). ВЫВОД : Период колебания пружинного маятника не зависит от температуры.

14

О БОБЩЕНИЕ В результате экспериментов мы выяснили, что период колебаний пружинного маятника зависит от массы тела, жёсткости пружины и не зависит от амплитуды колебаний и температуры.

15

Л ИТЕРАТУРА : Учебник по физике для 9 класса средней школы Н.М. Шахмаева, С.Н. Шахмаева, Д.Ш. Шодиева,-М. Просвещение.1990г. Кикоин И.К., Кикоин А.К. Физика. Учебник для 9кл.-М. Просвещение, 1990г. Громов С.В., Родина Н.А.. Физика. Учеб. Для 8кл.-М. Просвещение. 2000г. Сеть Интернет.

Звук

Звук – это колебания упругой среды, воспринимаемые органом слуха.

Условия, необходимые для возникновения и ощущения звука:

• наличие источника звука;
• наличие упругой среды между источником и приемником звука;
• наличие приемника звука; • частота колебаний должна лежать в звуковом диапазоне;
• мощность звука должна быть достаточной для восприятия.

Звуковые волны – это упругие волны, вызывающие у человека ощущение звука, представляющие собой зоны сжатия и разряжения, передающиеся на расстояние с течением времени.

Классификация звуковых волн:

• инфразвук (​\( \nu \)​ < 16 Гц);
• звуковой диапазон (16 Гц < \( \nu \) < 20 000 Гц);
• ультразвук (\( \nu \) > 20 000 Гц).

Скорость звука – это скорость распространения фазы колебания, т. е. области сжатия и разряжения среды.

Скорость звука зависит

от упругих свойств среды:

в воздухе – 331 м/с, в воде – 1400 м/с, в металле – 5000 м/с;

от температуры среды:

в воздухе при температуре 0°С – 331 м/с,
в воздухе при температуре +15°С – 340 м/с.

Характеристики звуковой волны

• Громкость – это величина, характеризующая слуховые ощущения человека, зависящая от амплитуды колебаний в звуковой волне. Единицы измерения – дБ (децибел).
• Высота тона – это величина, характеризующая слуховые ощущения человека, зависящая от частоты колебаний в звуковой волне. Чем больше частота, тем выше звук. Чем меньше частота, тем ниже звук.
• Тембр – это окраска звука.

Музыкальный звук – это звук, издаваемый гармонически колеблющимся телом. Каждому музыкальному тону соответствует определенная длина и частота звуковой волны.Шум – хаотическая смесь тонов.

Виды пружинного маятника

Выделяют несколько различных видов пружинного маятника. Стоит учитывать, что классификация может проводится по типу устанавливаемой пружины. Среди особенностей отметим:

1. Довольно большое распространение получили вертикальные колебания, так как в этом случае на груз не оказывается сила трения и другое воздействие. При вертикальном расположении груза существенно увеличивается степень воздействия силы тяжести. Распространен этот вариант исполнения при проведении самых различных расчетов. За счет силы тяжести есть вероятность того, что тело в исходной точке будет совершать большое количество инерционных движений. Этому также способствует упругость и инерция движения тела в конце хода.
2. Также применяется горизонтальный пружинный маятник. В этом случае груз находится на опорной поверхности и на момент перемещения также возникает трение. При горизонтальном расположении сила тяжести работает несколько иначе. Горизонтальное расположение тела получило широкое распространение в различных задачах.

Рассчитывается движение пружинного маятника можно при использовании достаточно большого количества различных формул, который должны учитывать воздействие всех сил. В большинстве случаев устанавливается классическая пружина. Среди особенностей отметим следующее:

1. Классическая витая пружина сжатия сегодня получила весьма широкое распространение. В этом случае между витками есть пространство, которое называется шагом. Пружина сжатия может и растягиваться, но зачастую она для этого не устанавливается. Отличительной особенностью можно назвать то, что последние витки выполнены в виде плоскости, за счет чего обеспечивается равномерное распределения усилия.
2. Может устанавливаться вариант исполнения для растяжения. Он рассчитан на установку в случае, когда приложенное усилие становится причиной увеличения длины. Для крепления проводится размещение крючков.

Распространены оба варианта исполнения

При этом важно уделить внимание тому, чтобы сила прикладывалась параллельно оси. В противном случае есть вероятность смещения витков, что становится причиной возникновения серьезных проблем, к примеру, деформации

2.2. Свободные колебания. Пружинный маятник window.top.document.title = “2.2. Свободные колебания. Пружинный маятник”;

Свободные колебания совершаются под действием внутренних сил системы после того, как система была выведена из положения равновесия.

Для того, чтобы свободные колебания совершались по гармоническому закону, необходимо, чтобы сила, стремящаяся возвратить тело в положение равновесия, была пропорциональна смещению тела из положения равновесия и направлена в сторону, противоположную смещению (см. §2.1):

В этом соотношении ω – круговая частота гармонических колебаний. Таким свойством обладает упругая сила в пределах применимости закона Гука:

Силы любой другой физической природы, удовлетворяющие этому условию, называются квазиупругими.

Таким образом, груз некоторой массы m, прикрепленный к пружине жесткости k, второй конец которой закреплен неподвижно (рис. 2.2.1), составляют систему, способную в отсутствие трения совершать свободные гармонические колебания. Груз на пружине называют линейным гармоническим осциллятором.

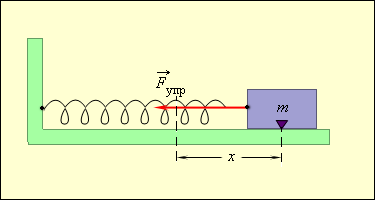Рисунок 2.2.1.Колебания груза на пружине. Трения нет

Круговая частота ω свободных колебаний груза на пружине находится из второго закона Ньютона:

Частота ω называется собственной частотой колебательной системы.

Период T гармонических колебаний груза на пружине равен

При горизонтальном расположении системы пружина–груз сила тяжести, приложенная к грузу, компенсируется силой реакции опоры. Если же груз подвешен на пружине, то сила тяжести направлена по линии движения груза. В положении равновесия пружина растянута на величину x, равную

ωT

Строгое описание поведения колебательной системы может быть дано, если принять во внимание математическую связь между ускорением тела a и координатой x: ускорение является второй производной координаты тела x по времени t:

Поэтому второй закон Ньютона для груза на пружине может быть записан в виде

Все физические системы (не только механические), описываемые уравнением (*), способны совершать свободные гармонические колебания, так как решением этого уравнения являются гармонические функции вида

Уравнение (*) называется уравнением свободных колебаний

Следует обратить внимание на то, что физические свойства колебательной системы определяют только собственную частоту колебаний ω или период T. Такие параметры колебательного процесса, как амплитуда xm и начальная фаза φ, определяются способом, с помощью которого система была выведена из состояния равновесия в начальный момент времени

Если, например, груз был смещен из положения равновесия на расстояние Δl и затем в момент времени t = 0 отпущен без начальной скорости, то xm = Δl, φ = 0

Если, например, груз был смещен из положения равновесия на расстояние Δl и затем в момент времени t = 0 отпущен без начальной скорости, то x_m = Δl, φ = 0.

Если же грузу, находившемуся в положении равновесия, с помощью резкого толчка была сообщена начальная скорость то ,

Таким образом, амплитуда x_m свободных колебаний и его начальная фаза φ определяются начальными условиями.

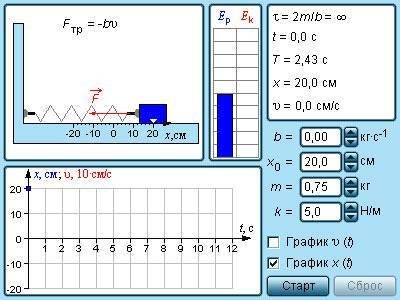Модель. Колебания груза на пружине

Существует много разновидностей механических колебательных систем, в которых используются силы упругих деформаций. На рис. 2.2.2 показан угловой аналог линейного гармонического осциллятора, совершающий крутильные колебания. Горизонтально расположенный диск висит на упругой нити, закрепленной в его центре масс. При повороте диска на угол θ возникает момент сил M_упр упругой деформации кручения:

Это соотношение выражает закон Гука для деформации кручения. Величина χ аналогична жесткости пружины k. Второй закон Ньютона для вращательного движения диска записывается в виде (см. §1.23)

I = I_Cε

По аналогии с грузом на пружине можно получить:

Крутильный маятник широко используется в механических часах. Его называют балансиром. В балансире момент упругих сил создается с помощью спиралевидной пружинки.

Рисунок 2.2.2.Крутильный маятник

Сила упругости в пружинном маятнике

Следует учитывать тот момент, что до деформирования пружины она находится в положении равновесия. Приложенная сила может приводить к ее растягиванию и сжиманию. Сила упругости в пружинном маятнике рассчитывается в соответствии с тем, как воздействует закон сохранения энергии. Согласно принятым нормам возникающая упругость пропорциональна смещению тела. В этом случае кинетическая энергия рассчитывается по формуле: F=-kx. В данном случае применяется коэффициент жесткости пружины.

Выделяют довольно большое количество особенностей воздействия силы упругости в пружинном маятнике. Среди особенностей отметим:

1. Максимальная сила упругости возникает на момент, когда тело находится на максимальном расстоянии от положения равновесия. При этом в подобном положении отмечается максимальное значение ускорение тела. Не следует забывать о том, что может проводится растягивание и сжатие пружины, оба варианта несколько отличается. При сжатии минимальная длина изделия ограничивается. Как правило, она имеет длину, равную диаметру витка умноженное на количество. Слишком большое усилие может стать причиной смещения витков, а также деформации проволоки. При растяжении есть момент удлинения, после которого происходит деформация. Сильное удлинение приводит к тому, что возникающей силы упругости недостаточно для возврата изделия в первоначальное состояние.
2. При сближении тела к месту равновесия происходит существенное уменьшение длины пружины. За счет этого наблюдается постоянное снижение показателя ускорения. Все это происходит за счет воздействия усилия упругости, которая связано с типом применяемого материала при изготовлении пружины и ее особенностями. Длина уменьшается за счет того, что расстояние между витками снижается. Особенностью можно назвать равномерное распределение витков, лишь только в случае дефектов есть вероятность нарушения подобного правила.
3. На момент достижения точки равновесия сила упругости снижается до нуля. Однако, скорость не снижается, так как тело движется по инерции. Точка равновесия характеризуется тем, что длина изделия в ней сохраняется на протяжении длительного периода при условии отсутствия внешнего деформирующего усилия. Точка равновесия определяется в случае построения схемы.
4. После достижения точки равновесия возникающая упругость начинает снижать скорость перемещения тела. Она действует в противоположном направлении. При этом возникает усилие, которое направлено в обратную сторону.
5. Дойдя крайней точки тело начинает двигаться в противоположную сторону. В зависимости от жесткости установленной пружины подобное действие будет повторятся неоднократно. Протяженность этого цикла зависит от самых различных моментов. Примером можно назвать массу тела, а также максимальное приложенное усилие для возникновения деформации. В некоторых случаях колебательные движения практически незаметны, но они все же возникают.

Приведенная выше информация указывает на то, что колебательные движения совершаются за счет воздействия упругости. Деформация происходит за счет приложенного усилия, которое может варьировать в достаточно большом диапазоне, все зависит от конкретного случая.

Максимальная кинетическая энергия груза на пружине

Свободные колебания совершаются под действием внутренних сил системы после того, как система была выведена из положения равновесия.

Для того, чтобы свободные колебания совершались по гармоническому закону, необходимо, чтобы сила, стремящаяся возвратить тело в положение равновесия, была пропорциональна смещению тела из положения равновесия и направлена в сторону, противоположную смещению:

В этом соотношении ω – круговая частота гармонических колебаний. Таким свойством обладает упругая сила в пределах применимости закона Гука:

Силы любой другой физической природы, удовлетворяющие этому условию, называются квазиупругими .

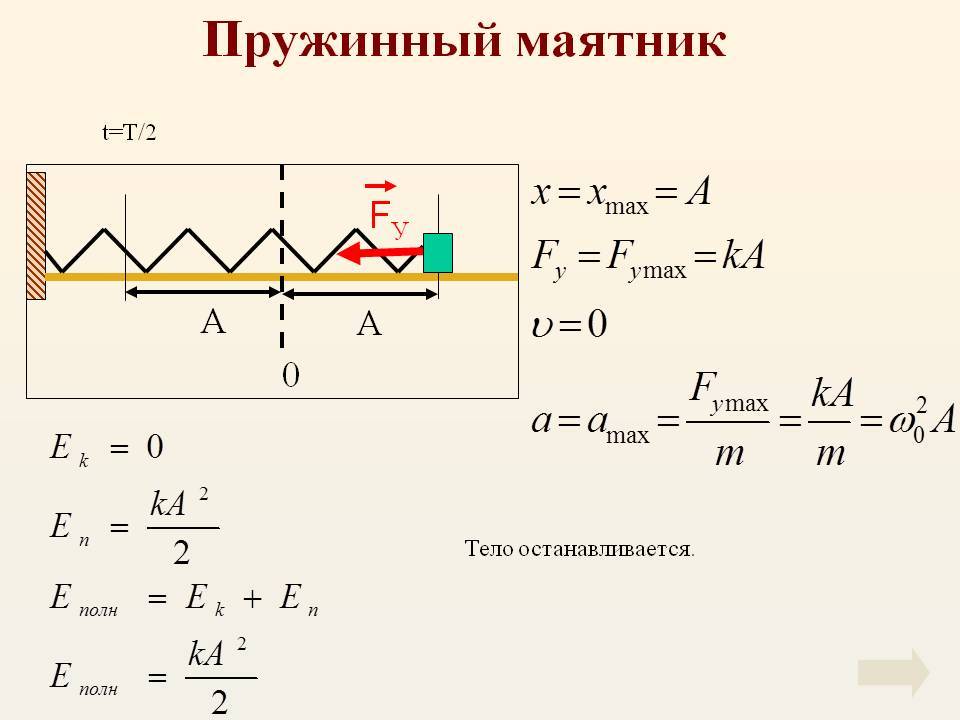
При свободных механических колебаниях кинетическая и потенциальная энергии изменяются периодически. При максимальном отклонении тела от положения равновесия его скорость, а следовательно, и кинетическая энергия обращаются в нуль. В этом положении потенциальная энергия колеблющегося тела достигает максимального значения. Для груза на горизонтально расположенной пружине потенциальная энергия – это энергия упругих деформаций пружины.

Когда тело при своем движении проходит через положение равновесия, его скорость максимальна. В этот момент оно обладает максимальной кинетической и минимальной потенциальной энергией. Увеличение кинетической энергии происходит за счет уменьшения потенциальной энергии. При дальнейшем движении начинает увеличиваться потенциальная энергия за счет убыли кинетической энергии и т. д.

Таким образом, при гармонических колебаниях происходит периодическое превращение кинетической энергии в потенциальную и наоборот.

Если в колебательной системе отсутствует трение, то полная механическая энергия при свободных колебаниях остается неизменной.

Для груза на пружине:

Запуск колебательного движения тела осуществляется с помощью кнопки Старт . Остановить процесс в любой момент времени позволяет кнопка Стоп .

Графически показано соотношение между потенциальной и кинетической энергиями при колебаниях в любой момент времени

Обратите внимание, что в отсутствие затухания полная энергия колебательной системы остается неизменной, потенциальная энергия достигает максимума при максимальном отклонении тела от положения равновесия, а кинетическая энергия принимает максимальное значение при прохождении тела через положение равновесия

Задание 7. Верхний конец пружины идеального пружинного маятника неподвижно закреплён, как показано на рисунке. Масса груза маятника равна m, жёсткость пружины равна k. Груз оттянули вниз на расстояние x от положения равновесия и отпустили с начальной скоростью, равной нулю. Формулы А и Б позволяют рассчитать значения физических величин, характеризующих колебания маятника.

Установите соответствие между формулами и физическими величинами, значение которых можно рассчитать по этим формулам.

К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.

1) амплитуда колебаний скорости

2) циклическая частота колебаний

3) максимальная кинетическая энергия груза

4) период колебаний

А) Имеем пружинный маятник массой m и жесткостью пружины k, тогда период свободных колебаний этого маятника определяется по формуле

Б) Для пружинного маятника известны формулы кинетической энергии

Пру­жин­ный ма­ят­ник, со­сто­я­щий из груза и лёгкой пру­жи­ны, со­вер­ша­ет ко­ле­ба­ния. В мо­мент, когда груз на­хо­дит­ся в край­нем по­ло­же­нии, его не­мно­го под­тал­ки­ва­ют вдоль оси пру­жи­ны в на­прав­ле­нии от по­ло­же­ния

рав­но­ве­сия. Как в ре­зуль­та­те этого из­ме­ня­ют­ся мак­си­маль­ная ки­не­ти­че­ская энер­гия груза ма­ят­ни­ка и ча­сто­та его ко­ле­ба­ний?

Для каж­дой ве­ли­чи­ны опре­де­ли­те со­от­вет­ству­ю­щий ха­рак­тер из­ме­не­ния:

3) не из­ме­ня­ет­ся

За­пи­ши­те в таб­ли­цу вы­бран­ные цифры для каж­дой фи­зи­че­ской ве­ли­чи­ны. Цифры в от­ве­те могут по­вто­рять­ся.

Мак­си­маль­ная ки­не­ти­че­ская энер­гия груза ма­ят­ни­ка

Ча­сто­та ко­ле­ба­ний ма­ят­ни­ка

Груз под­толк­ну­ли от по­ло­же­ния рав­но­ве­сия, от­ку­да сле­ду­ет, что ам­пли­ту­да ко­ле­ба­ний груза уве­ли­чит­ся. При этом уве­ли­чит­ся также и мак­си­маль­ная по­тен­ци­аль­ная энер­гия пру­жи­ны. По за­ко­ну со­хра­не­ния энер­гии, это при­ве­дет к уве­ли­че­нию мак­си­маль­ной ки­не­ти­че­ской энер­гии груза ма­ят­ни­ка.

Пе­ри­од и ча­сто­та пру­жин­но­го ма­ят­ни­ка за­ви­сят толь­ко от массы груза и жест­ко­сти пру­жи­ны. Таким об­ра­зом, при уве­ли­че­нии ам­пли­ту­ды ко­ле­ба­ний груза, ча­сто­та ко­ле­ба­ний ма­ят­ни­ка не из­ме­нит­ся.

Что такое начальная фаза и как определить ее по графику колебаний

Отклоним качели на некоторый угол от равновесия и будем удерживать их в таком положении. Когда мы отпустим их, качели начнут раскачиваться. А старт колебаний произойдет из угла, на который мы их отклонили.

Такой, начальный угол отклонения, называют начальной фазой колебаний. Обозначим этот угол (рис. 7) какой-нибудь греческой буквой, например, \(\large \varphi_{0} \).

\(\large \varphi_{0} \left(\text{рад} \right) \) — начальная фаза, измеряется в радианах (или градусах).

Рис. 7. Угол отклонения качелей перед началом колебаний

Рассмотрим теперь, как величина \(\large \varphi_{0} \) влияет на график колебаний (рис. 8). Для удобства будем считать, что мы рассматриваем колебания, которые происходят по закону синуса.

Кривая, обозначенная черным на рисунке, начинает период колебаний из точки t = 0. Эта кривая является «чистым», не сдвинутым синусом. Для нее величину начальной фазы \(\large \varphi_{0} \) принимаем равной нулю.

Рис. 8. Вертикальное положение стартовой точки в момент времени t = 0 и сдвиг графика по горизонтали определяется начальной фазой

Вторая кривая на рисунке обозначена красным цветом. Начало ее периода сдвинуто вправо относительно точки t = 0. Поэтому, для красной кривой, начавшей новый период колебаний спустя время \(\large \Delta t\), начальный угол \(\large \varphi_{0} \) будет отличаться от нулевого значения.

Определим угол \(\large \varphi_{0} \) с помощью графика колебаний.

Обратим внимание (рис. 8) на то, что время, лежащее на горизонтальной оси, измеряется в секундах, а величина \(\large \varphi_{0} \) — в радианах

Значит, нужно связать формулой кусочек времени \(\large \Delta t\) и соответствующий ему начальный угол \(\large \varphi_{0} \).

Как вычислить начальный угол по интервалу смещения

Алгоритм нахождения начального угла состоит из нескольких несложных шагов.

• Сначала определим интервал времени, обозначенный синими стрелками на рисунке. На осях большинства графиков располагают цифры, по которым это можно сделать. Как видно из рис. 8, этот интервал \(\large \Delta t\) равен 1 сек.
• Затем определим период. Для этого отметим одно полное колебание на красной кривой. Колебание началось в точке t = 1, а закончилось в точке t =5. Взяв разность между этими двумя точками времени, получим значение периода.

\

Из графика следует, что период T = 4 сек.

Рассчитаем теперь, какую долю периода составляет интервал времени \(\large \Delta t\). Для этого составим такую дробь \(\large \displaystyle \frac{\Delta t }{T} \):

\

Полученное значение дроби означает, что красная кривая сдвинута относительно точки t = 0 и черной кривой на четверть периода.

Нам известно, что одно полное колебание — один полный оборот (цикл), синус (или косинус) совершает, проходя каждый раз угол \(\large 2\pi \). Найдем теперь, как связана найденная доля периода с углом \(\large 2\pi \) полного цикла.

Для этого используем формулу:

\

\(\large \displaystyle \frac{1}{4} \cdot 2\pi = \frac{\pi }{2} =\varphi_{0} \)

Значит, интервалу \(\large \Delta t\) соответствует угол \(\large \displaystyle \frac{\pi }{2} \) – это начальная фаза для красной кривой на рисунке.

В заключение обратим внимание на следующее. Начало ближайшего к точке t = 0 периода красной кривой сдвинуто вправо

То есть, кривая запаздывает относительно «чистого» синуса.

Чтобы обозначить запаздывание, будем использовать знак «минус» для начального угла:

\

Примечание: Если на кривой колебаний начало ближайшего периода лежит левее точки t = 0, то в таком случае, угол \(\large \displaystyle \frac{\pi }{2} \) имеет знак «плюс».

Примечания:

1. Физики начинают отсчет времени из точки 0. Поэтому, время в задачах будет величиной не отрицательной.
2. На графике колебаний начальная фаза \( \varphi_{0}\) влияет на вертикальный сдвиг точки, из которой стартует колебательный процесс. Значит, можно для простоты сказать, что колебания имеют начальную точку.

Благодаря таким допущениям график колебаний при решении большинства задач можно изображать, начиная из окрестности нуля и преимущественно в правой полуплоскости.